
- •Тема VII. Ряды
- •Необходимый признак.
- •Достаточные признаки сходимости рядов с положительными членами.
- •Если существует конечный и отличный от нуля предел , то рассматриваемые ряды (1) и (2) сходятся или расходятся одновременно.
- •Пример 1. Доказать сходимость ряда
- •Интегральный признак Коши
- •Тогда ряд и несобственный интегралсходятся или расходятся одновременно (т.Е. Из сходимости интеграла следует сходимость ряда и наоборот).
- •Знакопеременные ряды.
- •Знакочередующийся ряд сходится, если абсолютные величины его членов убывают, а общий член стремится к нулю, т.Е. Если выполняются следующие два условия:
- •Пример 1. Исследовать сходимость степенного ряда
- •Пример 2. Найти область сходимости ряда:
- •Решение.
- •Пример 4. Найти радиус и интервал сходимости степенного ряда
- •Пример 5. Найти радиус и интервал сходимости степенного ряда . Решение
- •Пример 6. Найти промежуток сходимости ряда
- •Таким образом, на концах интервала данный ряд расходится. Промежутком сходимости является интервал .
- •Пример 7 Найти область сходимости степенного ряда
- •Пример 8. Найти область сходимости степенного ряда
- •Разложение функций в степенные ряды
- •Приближенные вычисления с помощью рядов
- •1. Приближенное вычисление значений функций
- •2. Приближенное вычисление определенных интегралов
- •3. Приближенное решение задачи Коши для обыкновенного дифференциального уравнения
- •Ряд Фурье
Тема VII. Ряды
Признаки сходимости числовых положительных рядов.
Необходимый признак.
Определения.
Пусть задана бесконечная последовательность чисел: u1, u2, …, un, …
Построим из этой последовательности выражение: u1+ u2 + u3 +…+ un +…
Это выражение называется числовым рядом, где слагаемые u1, u2, u3,… называются членами ряда, а член un - его общим членом. Таким образом, можно сказать, что числовой ряд – это бесконечная сумма чисел
Числовой
ряд часто записывается в виде
![]() .
Сумма
конечного числа n
первых членов ряда называется n-ой
частичной
суммой
ряда:
.
Сумма
конечного числа n
первых членов ряда называется n-ой
частичной
суммой
ряда:
Sn = u1 + u2 + … + un
Если
существует конечный предел
![]() ,
то его
называют суммой
ряда и
говорят, что ряд сходится.
,
то его
называют суммой
ряда и
говорят, что ряд сходится.
Если
![]() не существует (или равен бесконечности),
то ряд суммы не имеет, т.е.расходится.
не существует (или равен бесконечности),
то ряд суммы не имеет, т.е.расходится.
Пример
1.
Написать первые четыре члена ряда с
общим членом
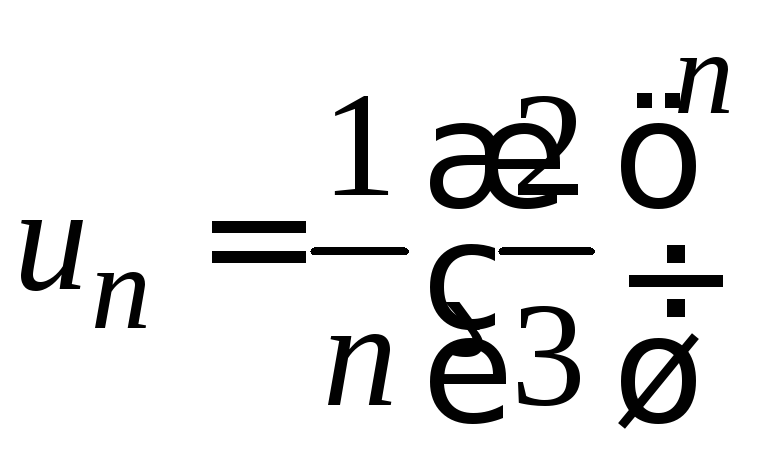 .
.
Решение. Полагая в формуле для общего члена n=1,2,3,4, получаем:
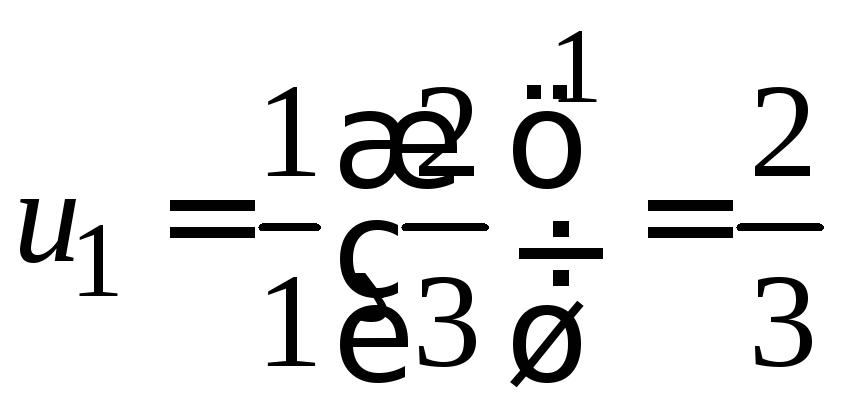 ;
;
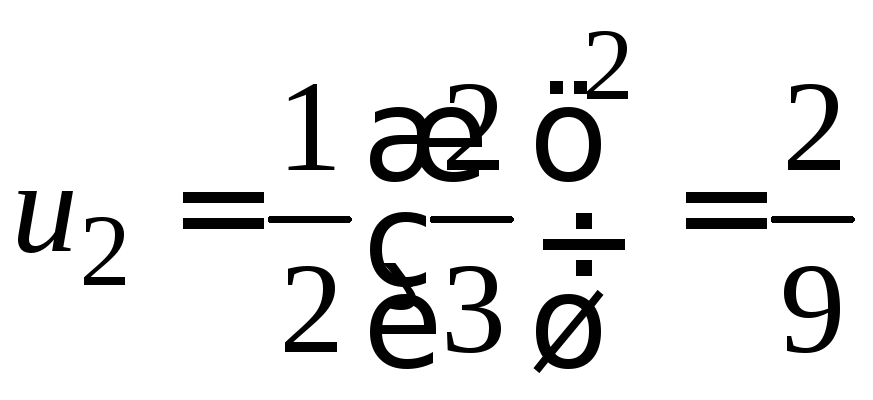 ;
;
 ;
;
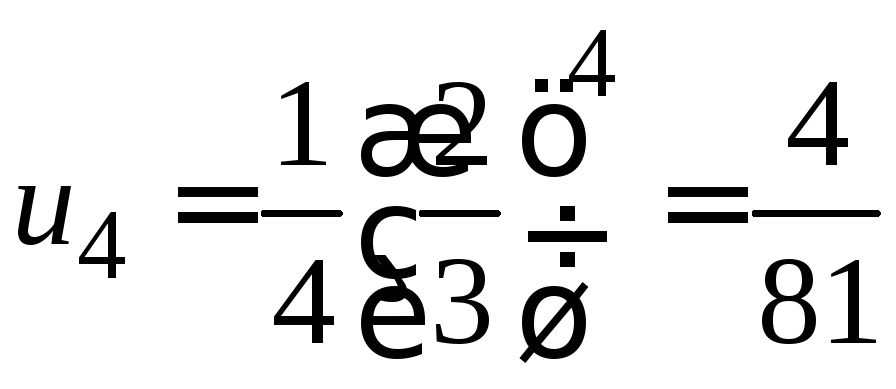
Итак,
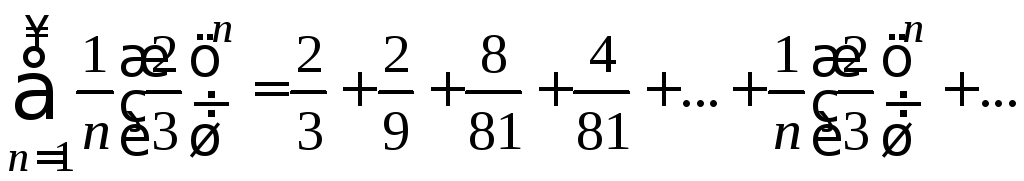
Пример
2.
Написать первые четыре члена ряда, общий
член которого задан формулой
![]() .
.
Решение. Полагая в данной формуле n=1,2,3,4,5,6, получаем
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Таким образом, данный ряд можно записать так:
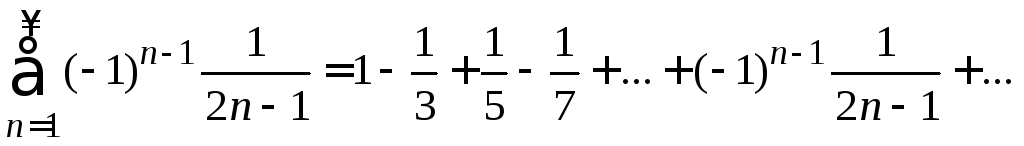
Пример 3. Найти формулу для общего члена ряда:
![]() ,
считая, что каждый его член получается
по тому закону, по которому образованы
записанные члены.
,
считая, что каждый его член получается
по тому закону, по которому образованы
записанные члены.
Решение.
Можно
заметить, что члены ряда – дроби,
числитель каждой из которых равен
единице (первый член тоже можно представить
так:
![]() ),
а знаменатель есть произведение нечётного
числа на соответствующую степень числа
2 (для первого члена это тоже верно:
),
а знаменатель есть произведение нечётного
числа на соответствующую степень числа
2 (для первого члена это тоже верно:![]() ).
).
Далее,
так как члены ряда имеют чередующиеся
знаки, нужно ввести множитель вида
![]() ,
чтобы получить искомую формулу:
,
чтобы получить искомую формулу: .
.
Замечание
1.
Перечисление членов ряда не всегда
может начинаться при n=1.
Часто первым является член ряда с номером
n=0
или, например, n=2.
В таком случае и записывают ряд в виде
![]() или
или![]()
Замечание 2. В формулах общего члена различных числовых рядов достаточно часто встречается знак факториала:
n!=1234…(n-1)n.
В частности, 1!=1, 2!=2, 3!=6 и т.д.; (n+1)!=n!(n+1). Считается, что 0!=1.
Иногда используют также знак двойного факториала четных и нечетных чисел:
(2n)!!=246…(2n-2)(2n). В частности, (2n+2)!!=(2n)!!(2n+2).
(2n+1)!!=135…(2n-1)(2n+1). В частности, (2n+3)!!=(2n+1)!!(2n+3).
Решить:
Написать первые четыре члена ряда:
A
1)
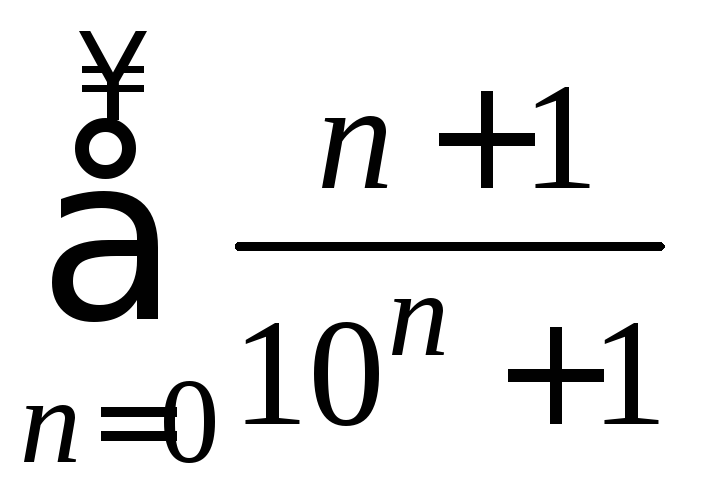 2)
2) 3)
3)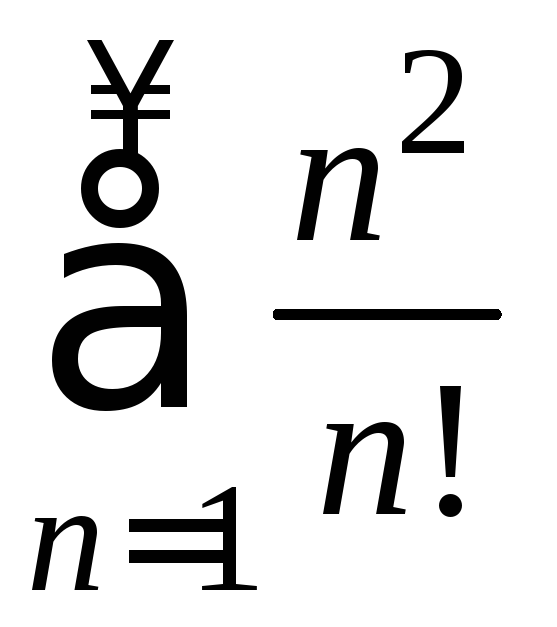 4)
4)
B
5)
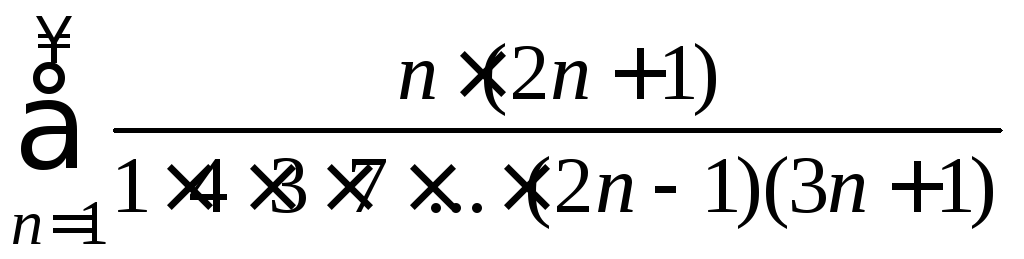 6)
6)
Написать простейшую формулу n-го члена ряда по указанным его первым членам и записать ряд, используя знак суммы ():
A
7)
![]() 8)
8)![]() 9)
9)![]()
10)
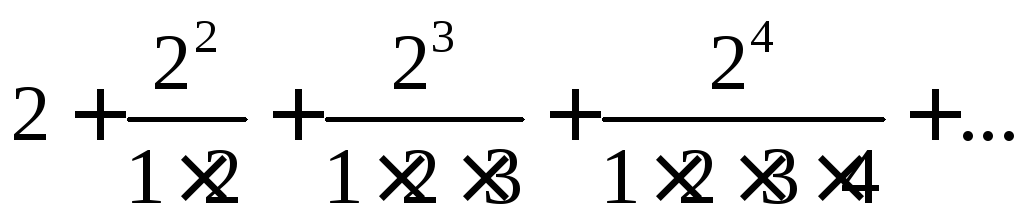 11)
11)![]()
B
12)
![]() 13)
13)![]()
14)![]() 15)
15)![]()
При исследовании
рядов основным вопросом является вопрос
о сходимости и расходимости ряда.
Непосредственное вычисление
![]() на практике не всегда выполнимо,
поэтому используются признаки, на
основании которых можно решить вопрос
о сходимости или расходимости ряда.
на практике не всегда выполнимо,
поэтому используются признаки, на
основании которых можно решить вопрос
о сходимости или расходимости ряда.
Следует отметить, что конечное число членов ряда влияет только на значение его суммы, но не на сам факт сходимости; таким образом, при исследовании ряда на сходимость мы можем, если нужно, отбросить первые несколько членов этого ряда.
Необходимый признак сходимости ряда
(т.е. условие, при невыполнении которого ряд расходится):
Если
ряд
 сходится, то его общий член стремится
к нулю при неограниченном возрастанииn,
т.е.
сходится, то его общий член стремится
к нулю при неограниченном возрастанииn,
т.е.
![]()
Следствие:
если общий член ряда не стремится к нулю при n→∞, то ряд расходится:
![]()
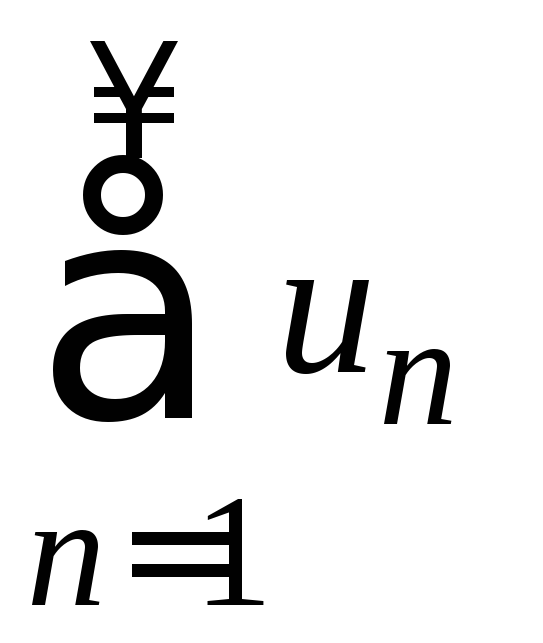 расходится
расходится
Указанный признак
является необходимым, но недостаточным.
Например, гармонический ряд:

расходится, хотя
![]() (расходимость гармонического ряда легко
доказать с помощью интегрального
признака – см. ниже)
(расходимость гармонического ряда легко
доказать с помощью интегрального
признака – см. ниже)
Пример
4.
Исследовать вопрос о поведении ряда с
помощью необходимого признака сходимости:
![]()
Решение.
Найдем предел общего члена ряда при n→
∞ (вспомним, что в этом случае можно
пренебречь младшими слагаемыми (степенями
n)
в числителе и знаменателе):
![]()
Данный ряд не удовлетворяет необходимому признаку сходимости и, следовательно, расходится.
Пример
5.
Проверить выполнимость необходимого
признака сходимости для ряда
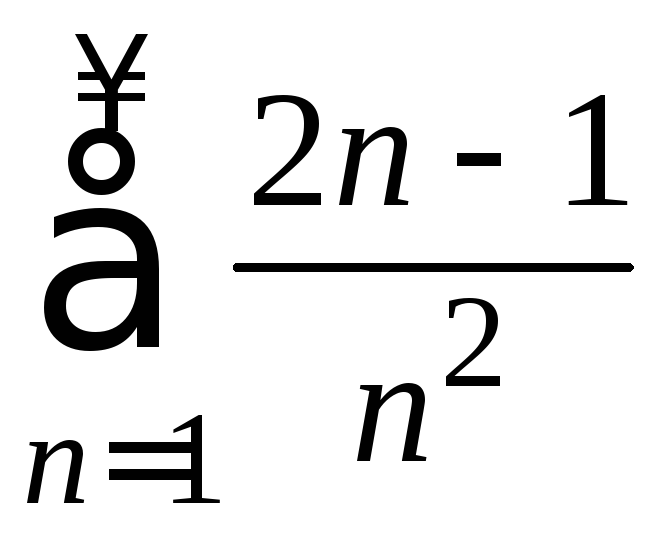
Решение.
Здесь
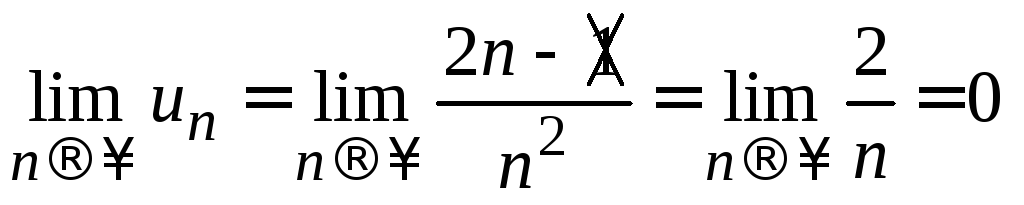 .
.
Необходимое условие сходимости ряда выполняется; сделать из этого вывод о том, сходится ряд или расходится, нельзя.
Решить:
A Проверить, выполняется ли необходимый признак сходимости для рядов:
1) 2)
2) 3)
3)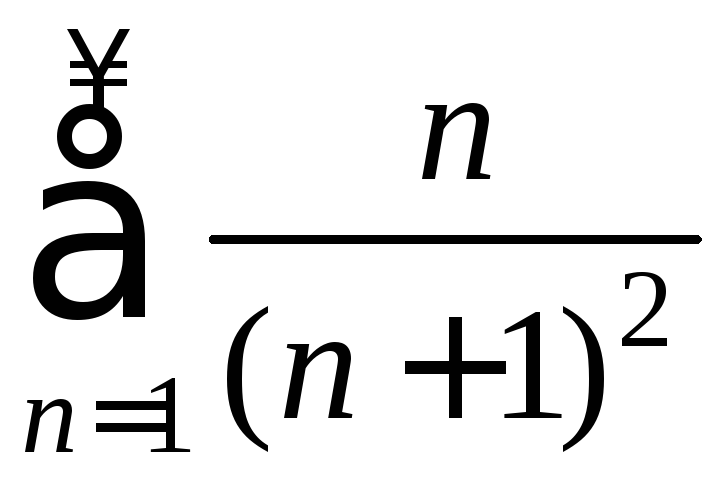 4)
4)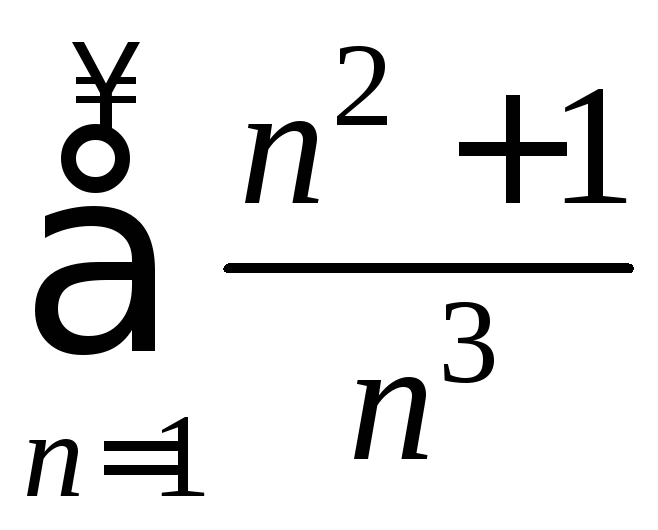
5)
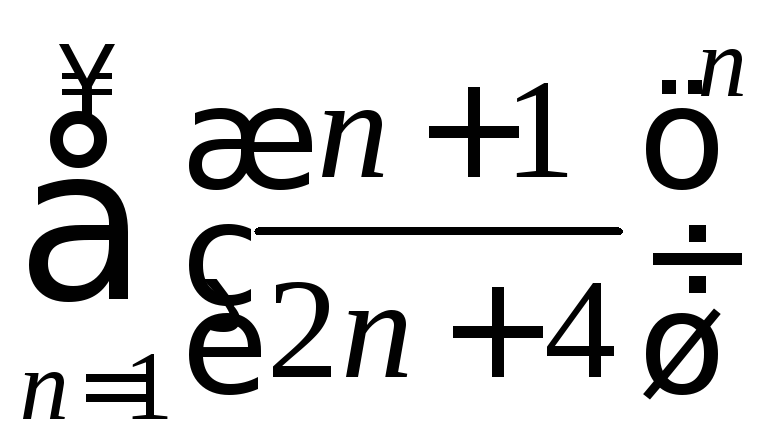 6)
6)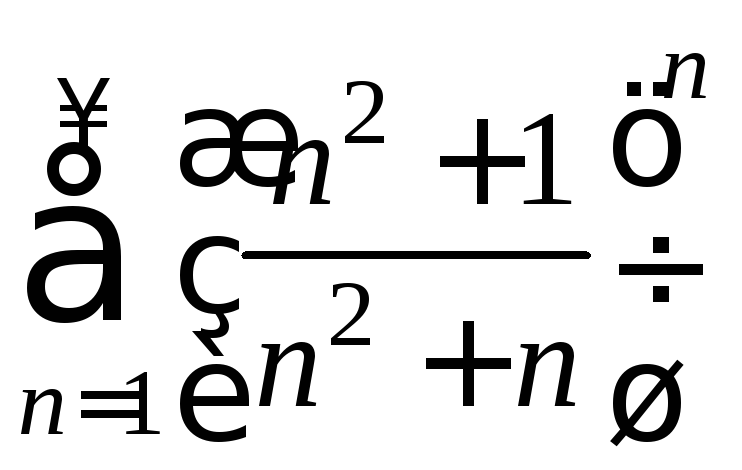 7)
7) 8)
8)
