15. Базисные функции частотно-временного анализа

Итак, частотно-временной анализ предназначен для выявления локальных частотно-временных возмущений сигнала. Вследствие кратковременности таких возмущений, сам сигнал может рассматриваться как заданный в L2 т.е. для одномерных сигналов – на всей действительной осис нормой. Следовательно, базисные функции, которые получили название вейвлетов, также должны принадлежать L2 и быстро убывать приТогда, чтобы перекрыть такими базисными функциями все возможные временные положения сигнала, необходимо, чтобы базисные функции представляли собой набор смещенных во времени функций. Удобнее всего, если этот набор образуется из одной и той же "материнской" функции(прототипа), сдвинутой по оси t т.е.Чтобы обеспечить частотный анализ, базисная функция должна иметь еще один аргумент – масштабный коэффициент, который является аналогом частоты в Фурье-анализе. Тогда базисные функции для частотно-временного анализа будут иметь видГде масштабный коэффициентвведен как делитель t, причем масштабированию подвергается также и сдвиг b. Это позволяет сохранить относительную "плотность" расположения базисных функций по оси t при расширении или сжатии самой функции и при(рис 3.6)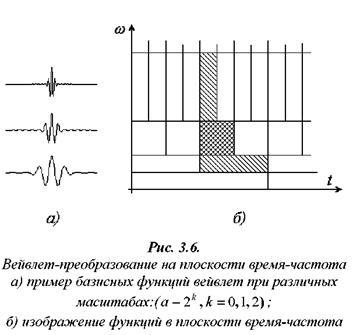Таким образом, базисные функции для частотно-временного анализа должны обладать следующими свойствами. Ограниченность, т.е. принадлежность L2. Локализация. Базисные функции вейвлет - анализа, в отличие от преобразования Фурье, должны быть локализованы, т.е. определены на конечном интервале как во временной, так и в частотной областях. Для этого достаточно, чтобы выполнялись условия: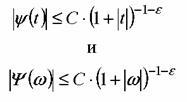Нулевое среднее. Равенство нулю нулевого моментаили, что иногда необходимо – равенство нулю момента m-го порядкаЭто – вейвлеты m-го порядка, позволяющие анализировать более тонкую структуру сигнала, подавляя медленно изменяющиеся его составляющие.

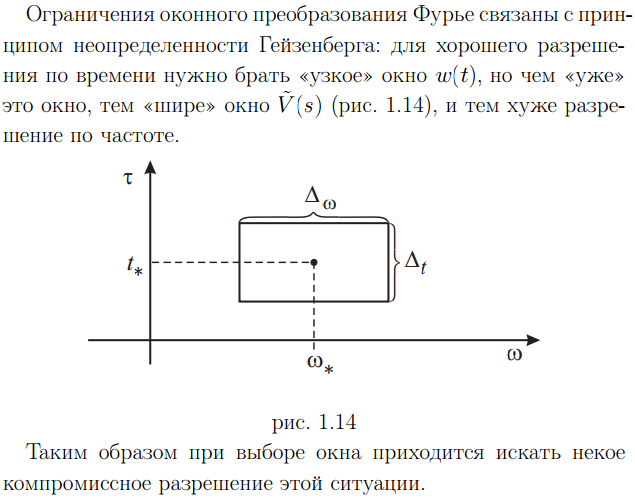
Оконное преобразование Фурье Полный временной интервал сигнала, особенно при большой его длительности, разделяется на подинтервалы – временные окна, и преобразование проводится последовательно для каждого окна в отдельности.  Тем самым осуществляется переход к частотно-временному (частотно-координатному) представлению сигналов и в какой-то мере позволяет выделять на координатной оси и анализировать особенности нестационарных сигналов.  Оконное преобразование выполняется в соответствии с выражением:

Функция представляет собой функцию окна сдвига преобразования по координате, где параметромзадаются фиксированные значения сдвига. При сдвиге окон с равномерным шагом. В качестве окна преобразования может использоваться как простейшее прямоугольное окно, так и специальные весовые окна (Бартлетта, Гаусса, Кайзера и пр.), обеспечивающие малые искажения спектра за счет граничных условий вырезки оконных отрезков сигналов и нейтрализующие явление Гиббса и специальное для конкретной за-дачи. Полученные выражения показывают, что интеграл Фурье можно рассматривать как аналог ряда Фурье: вместо суммирования по индексу, пробегающему целые значения, мы имеем интегрирование по непрерывно изменяющемуся переменному; вместо коэффициентов Фурье, зависящих от целого индекса, мы имеем функциииот непрерывно изменяющегося переменного. На практике ряд Фурье ограничивается определенным количеством членов. Ограничение числа членов ряда значениемозначает аппроксимацию бесконечномерного сигнала N-мерной системой базисных функций спектра сигнала с определенной погрешностью в зависимости от фактического спектра сигнала.

16. Базисные функции вейвлет-преобразования

Базисными функциями вейвлет-преобразований могут быть самые различные функции с компактным носителем - модулированные импульсами синусоиды, функции со скачками уровня и т.п. Они обеспечивает хорошее отображение и анализ сигналов с локальными особенностями, в том числе со скачками, разрывами и перепадами значений с большой крутизной.

Следует различать вейвлеты по целевым задачам вейвлетных преобразований с позиций декомпозиции – реконструкции сигналов. Было бы желательно иметь такое вейвлет-преобразование сигналов, которое обеспечивало бы полную информационную эквивалентность вейвлетного спектра сигналов временному (динамическому, координатному) представлению, и, соответственно, однозначность как декомпозиции сигналов, так и их реконструкции из вейвлетных спектров. Однако это возможно только при использовании ортогональных и биортогональных вейвлетов. Этим вейвлетам и будет уделено основное внимание. Для качественного анализа сигналов и локальных особенностей в сигналах может применяться более обширная номенклатура вейвлетных функций, которые хотя и не обеспечивают реконструкцию сигналов, но позволяют оценить информационное содержание сигналов и динамику изменения этой информации.

Определение вейвлета. К вейвлетам относятся локализованные функции, которые конструируются из одного материнского вейвлета(t) (или по любой другой независимой переменной) путем операций сдвига по аргументу (b) и масштабного изменения (а):

_ab(t) = (1/) ((t-b)/a), (a, b)ÎR, (t)ÎL²(R).

где множитель (1/) обеспечивает независимость нормы функций от масштабного числа 'a'.

Непрерывное вейвлет-преобразование сигнала s(t)ÎL²(R), которое применяется для качественного частотно-временного анализа, по смыслу соответствует преобразованию Фурье с заменой гармонического базисаexp(-jt) на вейвлетный((t-b)/a):

С(a, b) = ás(t), _ab(t)ñ = (1/)s(t)((t-b)/a) dt, (a, b)ÎR, a¹0.

Рис. 2.1.1. Вейвлеты Mhat и Wave.

Вейвлетный масштабно-временной спектр С(a,b) в отличие от фурье-спектра является функцией двух аргументов: масштаба вейвлета 'а' (в единицах, обратных частоте), и временного смещения вейвлета по сигналу 'b' (в единицах времени), при этом параметры 'а' и 'b' могут принимать любые значения в пределах областей их определения.

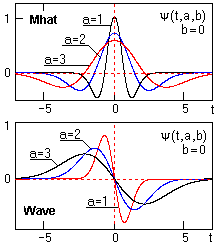
На рис. 2.1.1 приведены примеры простейших неортогональных вейвлетов четного (Mhat) и нечетного (Wave) типов.

Для количественных методов анализа (декомпозиция сигналов с возможностью последующей линейной реконструкции сигналов из обработанных вейвлет-спектров) в качестве вейвлетных базисов можно использовать любые локализованные функции (t), если для них существуют функции-двойники^#(t), такие, что семейства {_ab(t)} и {^_ab(t)} могут образовывать парные базисы функционального пространства L²(R). Вейвлеты, определенные таким образом, позволяют представить любую произвольную функцию в пространстве L²(R) в виде ряда:

s(t) = С(a,b)^_ab(t), (a, b)ÎI,

где коэффициенты С(a,b) – проекции сигнала на вейвлетный базис пространства, которые определяются скалярным произведением

С(a,b) = ás(t), _ab(t)ñ =s(t)_ab(t) dt.

Если вейвлет (t) обладает свойством ортогональности, то^(t) ≡(t) и вейвлетный базис ортогонален. Вейвлет может быть неортогональным, однако если он имеет двойника, и пара ((t), ^(t)) дает возможность сформировать семейства {_mk(t)} и {^_zp(t)}, удовлетворяющие условию биортогональности на целых числахI:

á_mk(t), ^_zp(t)ñ=_mz·_kp, m,k,z,pÎI,

то возможно разложение сигналов на вейвлетные ряды с обратной формулой реконструкции.

Свойства вейвлета,

• Локализация.Вейвлет должен быть непрерывным, интегрируемым, иметь компактный носитель и быть локализованным как во времени (в пространстве), так и по частоте. Если вейвлет в пространстве сужается, то его "средняя" частота повышается, спектр вейвлета перемещается в область более высоких частот и расширяется. Этот процесс должен быть линейным – сужение вейвлета вдвое должно повышать его "среднюю" частоту и ширину спектра также вдвое.

Вейвлетную функцию можно считать хорошо локализованной при выполнении условий:

(t) ≤C/(1+|t|)^1+,(f) ≤C/(1+|f|)^1+, С=const, при> 0.

• Нулевое среднее значение, т.е. выполнение условия для нулевого момента:

(t) dt = 0,

что обеспечивает выделение локальных особенностей сигналов в пределах вейвлетного носителя на уровне региональных изменений и тренда, нулевое усиление постоянной составляющей сигналов, нулевое значение частотного спектра вейвлета при =0, и локализацию спектра вейвлета в виде полосового фильтра с центром на определенной (доминирующей) частоте₀. Для анализа мелкомасштабных флюктуаций и особенностей высокого порядка, как правило, требуются и нулевые значения определенного количества последующих моментов:

t^m(t) dt = 0.

Такие вейвлеты называются вейвлетами m-го порядка.

• Ограниченность.Необходимое и достаточное условие:

||(t)||²=|(t)|²dt <¥

Оценка ограниченности и локализации может выполняться с использованием выражений:

|(t)| < 1/(1+|t|ⁿ), или |(ω)| < 1/(1+|ω_o|ⁿ),

где _o– средняя частота вейвлета. Числоn должно быть как можно больше.

• Автомодельность базисаили самоподобие. Форма всех базисных вейвлетов_ab(t) должна быть подобна материнскому вейвлету(t), т.е. должна оставаться одной и той же при сдвигах и масштабировании (растяжении/сжатии), иметь одно и то же число осцилляций.