Перечень билетов с вопросами, выносимых на экзамен

1. Методы моделирования с использованием рациональной передаточной функции. Подходы к моделированию и идентификации параметров. АР-, СС- и АРСС-модели случайных процессов. Соотношения между параметрами АР-, СС- и АРСС-моделей.

2. Соотношение АР-, СС- и АРСС-параметров с автокорреляционной последовательностью.Уравнения Юла-Уокера.

3. Спектральная факторизация.Связь параметров АР-модели с фильтрами линейного предсказания.Алгоритм Левинсона. Коэффициенты отражения.

4. Свойства спектральной плотности мощности авторегрессионного процесса.Спектральное оценивание на основе метода максимальной энтропии. Автокорреляционное обобщение АР-оценки.

5. АР-оценивание параметров. Групповая оценка АР-параметров. Геометрический алгоритм. Гармонический алгоритм (Берга).

6. Оценивание линейного предсказания по методу наименьших квадратов. Характеристики оценок. Выбор порядка АР-модели.

7. Метод Прони. Исходный подход Прони. Метод наименьших квадратов Прони. Спектр Прони. Оценивание спектральных линий по методу Прони.

8. Спектральное оценивание с помощью метода максимального правдоподобия Кейпона ( по методу минимума дисперсии ).

9. Методы оценивания частоты, основанные на анализе собственных значений. Метод MUSIC.

10. Метод гармонического разложения Писаренко.

11. Оценивание частот суммы нескольких синусоид: Модификация метода линейного предсказания (Тафтас).

12. Корректный подход к непараметрическому оцениванию СПМ. (Д.Дж.Томсон). МТМ-метод.

13. Биспектральное оценивание. Свойства биспектра. Обычные методы биспектрального оценивания. Применение биспектра.

14. Кепстр и его применение при обработке данных. Кепстр мощности. Комплексный кепстр. Фазовый кепстр.

15. Частотно-временные свойства базисных функций. Оконное преобразование Фурье. Принцип неопределенности.

16. Базисные функции частотно-временного анализа. Непрерывное вейвлет-преобразование.

17. Свойства непрерывного вейвлет-преобразования.

18. Дискретное вейвлет-преобразование. Дискретизация масштаба. Дискретизация масштаба и сдвига.

1. Методы моделирования с использованием рациональной передаточной функции. Подходы к моделированию и идентификации параметров. АР-, СС- и АРСС-модели случайных процессов. Соотношения между параметрами АР-, СС- и АРСС-моделей.

Моделируемое линейное устройство (узел) может быть описано с помощью передаточной функции K(p). Передаточная функцияK(p)может быть дробно-рациональной функцией комплексной частотыр, если узел выполнен на элементах с сосредоточенными параметрами:

, (2)

где и- действительные числа.

Передаточная функция (2) может быть также представлена в эквивалентной форме:

, (3)

где - нули числителя (2) (нули),

- нули знаменателя (2) (полюсы).

Линейный узел может быть также описан с помощью импульсной характеристики . Передаточная функцияи импульсная характеристикаоднозначно связаны друг с другом, так как составляют пару преобразования Лапласа.

Если - дробно-рациональная функцияp(2,3), то в случае когда полюсыпростые справедливо

, (4)

где

. (5)

Параметрический метод спектрального оценивания состоит из трех этапов. На первом из них производится выбор параметрической модели временного ряда, соответствующий имеющейся записи измеренных данных. В этой главе будут рассмотрены три типа параметрических моделей временных рядов: авторегрессионная (АР) модель, модель скользящего среднего (СС) и комбинированная модель авторегрессии - скользящего среднего (АРСС). На втором этапе вычисляются оценки параметров модели. На третьем этапе оцененные значения параметров вводятся в теоретическое выражение для спектральной плотности мощности, соответствующее избранной модели.

АР-, СС- и АРСС-модели случайных процессов

Модель временного ряда, которая пригодна для аппроксимации многих встречающихся на практике детерминированных и стохастических процессов с дискретным временем, описывается выходом фильтра, выражаемым следующим линейным разностным уравнением с комплексными коэффициентами:

(6.1)

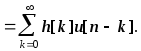(6.2)

Здесь x[n] - последовательность на выходе казуального фильтра (h[k]=0 при k0), который формирует наблюдаемые данные, а u[n] - входная возбуждающая последовательность. Без потери общности можно положить b[0]=1, так как вход u[n] всегда можно соответствующим образом промасштабировать, с тем чтобы учесть любой коэффициент усиления фильтра. Выше было показано, что системная функция H(z) , связывающая вход и выход этого фильтра имеет рациональную форму

H(z) = (6.3)

в которой полиномы определяются следующими выражениями:

A(z) = 1 + (6.4)

B(z) = 1 + (6.5)

H(z) = 1+ (6.6)

При этом предполагается, что нули полиномов A(z) и B(z) расположены внутри единичной окружности в z-плоскости, с тем чтобы гарантировать принадлежность функции H(z) устойчивому минимально-фазовому казуальному фильтру.

Согласно выражениям z-преобразование автокорреляции выходной последовательности x[n] и z-преобразование автокорреляции входного случайного процесса u[n] связаны соотношением

P_xx (z) = P_uu (z)H(z)H^(1/z^) = P_uu (z) [B(z)B^(1/z^)] / [A(z)A^(1/z^)]. (6.7)

Входной возбуждающий процесс u[n] обычно не доступен для наблюдения и поэтому не может быть использован для целей спектрального анализа. Относительно него можно принять много различных допущений, скажем положить, что это единичный u[n] импульс, импульсная последовательность или белый шум. Если, например, использовано допущение о том, что это - импульс, то мы приходим к методам, которые описаны в гл.11. В данной главе мы будем полагать, что возбуждающая последовательность является белым шумом с нулевым средним значением и дисперсией p_w, так что P_uu(z)= p_w. Тогда модель авторегрессии-скользящего среднего (АРСС) для временного ряда будет определяться выражением, где u[n] - последовательность, соответствующая белому шуму. Функциональная схема АРСС-модели показана на рис.6.1,а; здесь параметры a[k] характеризуют авторегрессионную часть этой модели, а параметры b[k] - ее часть, соответствующую скользящему среднему. Спектральную плотность мощности для АРСС-модели получаем, подставляя в (6.7) z=exp(j2fT) и масштабируя интервалом отсчетов T, что дает

Р_АРСС(f) = T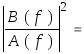_ T_ (6.8)

где полиномы A(f) и B(f) определяются выражениями

A(f) = 1 + (6.9)

B(f) = 1 +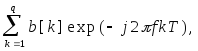

а векторы комплексных синусоид e_q(f) и e_p(f) и векторы параметров a и b имеют следующий вид:

e_p(f) = (6.10)

e_q(f) =

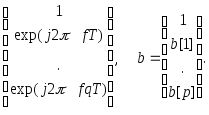
Спектральная плотность мощности АРСС-процесса вычисляется в диапазоне частот -1/2T f 1/2T.

В литературе часто используется обозначение АРСС(p,q), что удобно для краткого обозначения АРСС-модели с параметрами авторегрессии порядка p и параметрами скользящего среднего порядка q. Заметим, что задание АР-параметров, СС-параметров и дисперсии белого шума p_ полностью характеризуют спектральную плотность мощности АРСС-процесса x[n] . Любой аддитивный шум наблюдения, присутствующий в последовательности измеряемых данных, должен моделироваться как шум источника возбуждающего шума, являющегося составной частью АРСС-модели. Эффекты, обусловленные шумом наблюдения, обсуждаются в гл.8.

рисунки 6.2

Если все АР-параметры положить, за исключением a[0]=1, равными нулю, то тогда

x[n] = (6.11)

будет строго СС-процессом порядка q, или просто СС(q)-процессом. Полагая в уравнении (6.8) p=0, получаем спектральную плотность мощности СС-процесса

P_cc (f) =T_wT_w (6.12)

Функциональная схема СС-модели показана на рис.6.1,в.

Если все СС-параметры положить, за исключением b[0]=1, равными нулю, то

x[n] = - (6.13)

будет строго АР-процессом порядка р, или просто АР(р) - процессом. Полагая в уравнении (6.8) q=0, получаем спектральную плотность мощности АР-процесса:

P_АР (f) = (6.14)

Функциональная схема АР-модели показана на рис.6.1,г. При заданных значениях параметров и дисперсии белого шума _w спектральные плотности мощности АРСС-, СС-, АР-процессов можно вычислить с помощью подпрограммы ARMAPSD, приведенной в приложении 6.А.

На рис. 6.2 показаны спектры типичных АРСС-, СС-, АР-процессов. Отметим острые пики, характерные для АР-спектров, и глубокие провалы, характерные для СС-спектров. АРСС-спектр, показанный на рис.6.2,в представляет собой результат объединения АР- и СС-спектров, показанных на на рис.6.2,а и 6.2,б. АРСС-спектр пригоден для моделирования как острых пиков, так и глубоких провалов. С несколько иной трактовкой спектральных характеристик этих параметрических моделей можно познакомиться в статье Гутовски и др. [2] и книге Кея [3].

Соотношения между параметрами АР-, СС- и АРСС-моделей

Если задана АР-, СС- и АРСС-модель с конечным числом параметров, то ее можно представить через две другие модели. АРСС- и СС-процессы можно записать с помощью одной АР- модели в общем случае бесконечного порядка. Этот факт очень важен, так как позволяет выбирать любую из трех моделей и все же получать приемлемую аппроксимацию при достаточно большом порядке этой модели. Возможны определенные алгоритмические выгоды, если по имеющимся данным сначала оценить параметры какой-либо модели, а затем по ним вычислить значения параметров какой-либо другой модели. Много эффективных алгоритмов оценивания разработано, в частности, для АР- модели. Как будет показано в гл.10, оценивание параметров АР- модели большого порядка часто используется в качестве первого этапа алгоритма оценивания параметров СС- и АРСС-моделей.

Пусть

C(z) = 1 + (6.15)

- полином знаменателя АР()-модели. Параметры c[k] АР()-модели, которая эквивалентна АРСС (p, q )-модели, получаются из соотношения

(6.16)

или формированием обратного z-преобразования от C(z)B(z)= A(z). Отсюда получаем

c[n] = (6.17)

с начальными условиями c[-1] =...= c[-q] = 0. И наоборот, если заданы параметры АР()-модели, которая, как известно, эквивалентна АРСС (p, q )-модели, то значения СС-параметров можно восстановить, решая уравнение

(6.18)

относительно параметров b[k] и используя при этом соотношение (6.17) при Матрица параметров в уравнении (6.18) является тёплицевой, поэтому для его решения можно использовать подпрограмму TOEPLITZ , помещенную в приложении 3.Г. После определения СС-параметров значения АР-параметров АРСС-модели можно восстановить с помощью свертки

a[n] = c[n] + (6.19)

где Алгоритмы быстрой свертки основаны на использовании БПФ. Отметим также, что уравнение (6.19) выводится из уравнения (6.17).

Заметим, что в уравнениях (6.18) и (6.19) используются только авторегрессионные параметры c[1],...c[p+q] АР()-модели. Если параметры c[k] при kp+q полагаются равными нулю, то результирующая усеченная АР(p+q )-модель может аппроксимировать только ту АРСС(p+q )-модель, из которой она получена. Она аппроксимирует эту АРСС-модель в том смысле, что полином, обратный полиному АРСС-модели,

G(z) = (6.20)

и полином усеченной АР-модели

C(z) = 1+ (6.21)

согласованы, т.е. g[k] = c[k], только для .Эта аппроксимация рациональной функции полиномов конечного порядка полиномом более высокого порядка представляет собой известную задачу аппроксимации Паде . Эта процедура будет использована в гл.10 для вывода аппроксимаций АРСС-моделей высокого порядка. Типичные АР-аппроксимации высокого порядка для АРСС-модели низкого порядка показаны на рис.6.3.

Аналогичным образом пусть теперь

D(z) = 1+ (6.22)

- полином числителя СС()-модели. Параметрыb[k] этой модели, которая эквивалентна АРСС(p+q )-модели, можно определить, записывая уравнение

(6.23)

или формированием обратного -преобразования от D(z) A(z) = B(z). Отсюда получаем

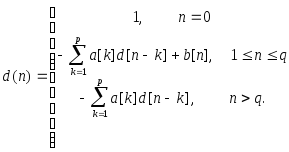(6.24)

2. Соотношение АР-, СС- и АРСС-параметров с автокорреляционной последовательностью. Уравнения Юла-Уокера.

Соотношение АР-, СС- и АРСС-параметров

с автокорреляционной последовательностью

Этот раздел посвящен определению параметров модели в том случае, когда известна автокорреляционная последовательность. Если обе части уравнения (6.1) помножить на x^ [n-m] и определить математическое ожидание, то получим

(6.25)

или

(6.26)

Взаимную корреляцию r_ux[i] между входом и выходом можно записать через параметры h[k], входящие в выражение (6.6), используя для этой цели уравнение (6.2),

что дает

(6.27)

Поскольку полагается, что u[k] - белый шум, то

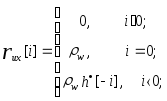(6.28)

Отсюда получаем окончательное выражение, связывающее параметры АРСС-модели и автокорреляционную последовательность процесса x[k]:

r_xx[m] = 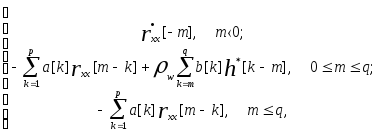(6.29)

где напомним читателю, что h[0] =1 по определению (см. уравнение (6.2)).

Авторегрессионные параметры АРСС-модели и автокорреляционная последовательность связаны системой линейных уравнений. Выражение (6.29) можно, например, записать для p значений индекса временного сдвига q+1  m  q+p и затем представить в матричной форме

(6.30)

Таким образом, если задана автокорреляционная последовательность для q-p+1  m  q+p , то АР-параметры можно найти отдельно от СС-параметров как решение системы линейных уравнений (6.30). Уравнения (6.30) называются нормальными уравнениями Юла-Уолкера для АРСС-процесса; иногда их также называют модифицированными уравнениями Юла-Уолкера. Автокорреляционная матрица в системе (6.30) является тёплицевой, поэтому для решения этой системы можно применить подпрограмму, помещенную в приложении 3.Г. Количество требуемых для решения вычислительных операций пропорционально величине p². Следует заметить, что значения СС-параметров АРСС-модели не являются, к сожалению, решением системы линейных уравнений. СС-параметры входят в выражение (6.29) в виде сверток с коэффициентами импульсной характеристики h[k], а это приводит к нелинейной связи автокорреляционной последовательностью.

Полагая в (6.29) q=0, получаем уравнение, связывающее авторегрессионную последовательность с параметрами авторегрессионной модели:

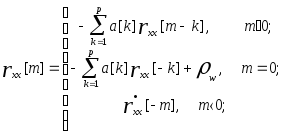(6.31)

Это выражение можно записать для p+1 значений индекса временного сдвига -0  m  p и затем представить в матричной форме

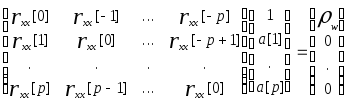(6.32)

Таким образом, если задана автокорреляционная последовательность для 0  m  p , то АР-параметры можно найти в результате решения уравнений (6.32), которые называются нормальными уравнениями Юла-Уолкера для АР-процесса. Автокорреляционная матрица в (6.32) является тёплицевой, и эрмитовой, поскольку r_xx[-k] = . Поэтому для получения решения p_w , a[1],..., a[p] при заданной АКП с 0  m  p можно использовать подпрограмму LEVINSON , помещенную в приложении 3.В. Количество требуемых для этого вычислительных операций пропорционально величине p².

Используя автокорреляционную последовательность, соответствующую уравнениям (6.31), получаем следующее выражение для СПМ авторегрессионного процесса:

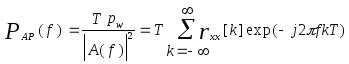. (6.33)

Заметим, что значения автокорреляции, соответствующие значениям индекса временного сдвига то 0 до p, однозначно описывают авторегрессионный процесс порядка p, поскольку значение автокорреляции при k  p получаются рекурсивно

(6.34)

что следует из выражения (6.29) при q=0. Полагая в (6.29) p=0 и замечая, что h[k]= b[k] при 1  k  q, получаем выражение, связывающее автокорреляционную последовательность с параметрами модели скользящего среднего

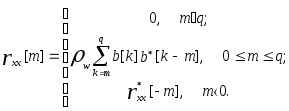(6.35)

Отсюда следует, что АКП и СС-параметры связаны нелинейным соотношением типа свертки. Используя далее автокорреляционную последовательность, соответствующую уравнениям (6.35), получаем выражение для СПМ процесса скользящего среднего

(6.36)

Заметим, что суммирование в (6.36) осуществляется в конечных пределах, что просто отражает тот факт, что процесс скользящего среднего порядка q некоррелирован при временных сдвигах k  q. Выражение (6.36) идентично по форме выражению для оценки СПМ, получаемой с помощью классического коррелограммного метода:

(6.37)

если используются автокорреляционные оценки для которых максимальное значение k равно q . Различие между этими двумя методами спектрального оценивания обусловлено тем, как в них используются имеющиеся данные. В коррелограммной методе данные используются непосредственно для получения оценки автокорреляционной последовательности. В методе скользящего среднего данные используются для получения оценок СС-параметров (см. гл.10, где описана процедура СС-оценивания), а затем с помощью выражения (6.12) вычисляется СПМ. Тем не менее оба метода дают спектры с одинаковыми свойствами.