3. Спектральная факторизация. Связь параметров ар-модели с фильтрами линейного предсказания. Алгоритм Левинсона. Коэффициенты отражения.

Спектральная факторизация

Рассмотрим z-преобразование АР(p)-процесса, которое, согласно (6.7), определяется выражением

(6.38)

где A(z)A^(1/z^) - полином по z порядка 2p . Полюсы в (6.38) будут комплексно-сопряженными взаимно обратными парами. Например, если z_k - корень полинома A(z), то (1/z_k)^=1/z_k^ будет корнем полинома A^(1/z^) . Если z_k лежит внутри единичной окружности, то 1/z_k^ будет расположен вне её. Кроме того, корни полинома A(z) также будут комплексно-сопряженными парами, если все коэффициенты этого полинома действительны.

Рассмотрим знаменатель в (6.38) - функцию A(z)A^(1/z^) . Типичная диаграмма расположения полюсов произведения полиномов A(z)A^(1/z^) показана на рис.6.5,а. Существует 2^р возможных комбинаций в случае p полюсов для полинома A(z), которые будут давать идентичный полином A(z)A^(1/z^) . На рис.6.5,б и рис.6.5,в показаны две вожможные спектральные факторизации полюсов полинома A(z)A^(1/z^), представленных на рис.6.5,а. Однозначная факторизация требует, чтобы модель временного ряда была и устойчивой, и казуальной, что предполагалось при записи уравнения (6.1). Согласно теории линейных систем (см.гл.2), полином A(z) должен быть расположены внутри единичной окружности в z-плоскости, как показано на рис.6.5,в. Поэтому все корни полинома A^(1/z^) будут расположены вне её. Полином A^(1/z^) ассоциируется с устойчивым антиказуальным авторегрессионным процессом

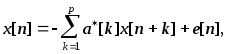(6.39)

определенным при n0, а не с казуальным АР-процессом, определенным при n0.

Заметим, что не следует путать устойчивость фильтра, связанную со спектральной факторизацией, и статистическую устойчивость. Устойчивость фильтра касается выбора АР- или СС-параметров, которые формируют автокорреляционные рекурсивные выражения, такие как (6.29) и (6.31). Статистическая устойчивость касается методов, которые позволяют уменьшить дисперсию спектральных оценок, получаемых по заданным конечным записям данных. В гл.8 будут описаны методы оценивания на основе линейного предсказания, которые обладают хорошей статистической устойчивостью, но не обязательно гарантируют получение минимально-фазовых оценок полинома A(z). С точки зрения оценки СПМ вовсе необязательно, чтобы полином A(z) являлся минимально-фазовым полиномом, поскольку оценка СПМ может быть получена по любому полиному A(z) с произвольным расположением корней, как показано на рис. 6.5. Вопрос устойчивости вознакает в том случае, когда для реализации фильтра требуются оценки коэффициентов полинома A(z). В этом случае случае минимально-фазовый фильтр может быть создан посредством инверсного переноса переноса всех полюсов полинома A(z), расположенных вне единичной окружности, внутрь ее. Иными словами, нужно просто сформировать A(z)A^(1/z^) и выполнить минамально-фазовую факторизацию.

4Свойства спектральной плотности мощности авторегрессионного процесса. Спектральное оценивание на основе метода максимальной энтропии. Автокорреляционное обобщение ар-оценки.

Авторегрессионное спектральное оценивание

Одна из причин применения параметрических моделей случайных и процессов и построения на их основе методов получения оценок спектральной плотности мощности обусловлена увеличением точности оценок по сравнению с классическими методами. Еще одна важная причина - более высокое спектральное разрешение. Далее рассматриваются следующие методы: метод Юла-Уалкера оценивания авторегрессионных параметров по последовательности оценок автокорреляционной функции и метод Берга оценивания авторегрессионных параметров по последовательности оценок коэффициентов отражения.

Модель временного ряда (называемая модели авторегрессии-скользящего среднего (АРСС) в случае входной последовательности - белого шума), которая пригодна для аппроксимации многих встречающихся на практике детерминированных и стохастических процессов с дискретным временем, описывается следующим разностным уравнением

. (2.1)

Системная функция , связывающая вход и выход этого фильтра имеет рациональную форму

. (2.2)

Если в качестве входной последовательности использовать белый шум, то приходим к АРСС-модели. Спектральную плотность для АРСС-модели получаем, подставляя , что дает

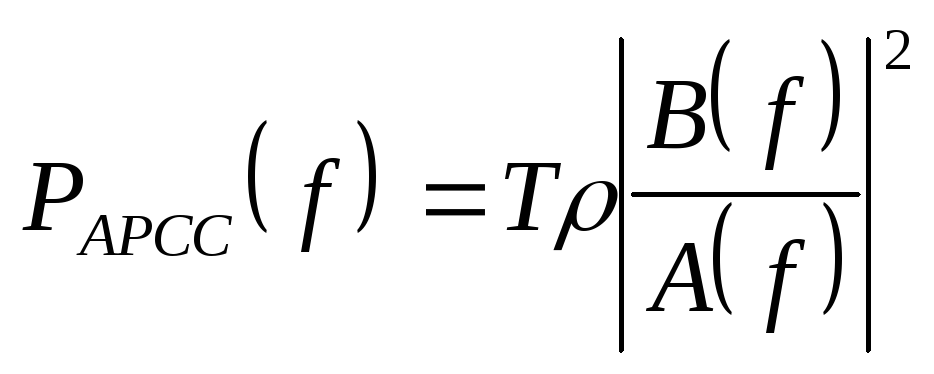, (2.3)

где ,

,, а- дисперсия

возбуждающего белого шума

В частных случаях для авторегрессионной модели и модели скользящего среднего получаем соответственно

, (2.4)

. (2.5)

Оценивание корреляционной функции - метод Юла-Уалкера

Из соотношения, связывающего параметры АРСС-модели с порядком авторегрессии p и скользящего среднего q

. (2.6)

Поскольку полагается, что u[k] - белый шум, то

,, (2.7)

, m>q, (2.8)

, m<0. (2.9)

В частном случае для авторегрессионных параметров, получаем

,, (2.10)

, m=0, (2.11)

, m<0. (2.12)

В матричном виде эти соотношения выглядят следующим образом

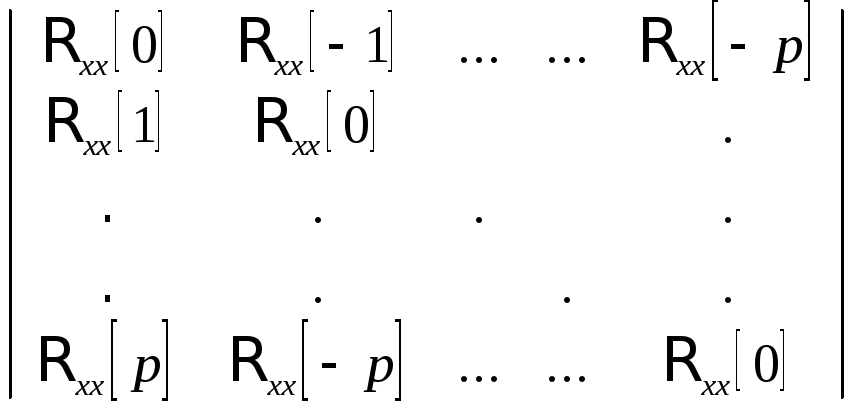
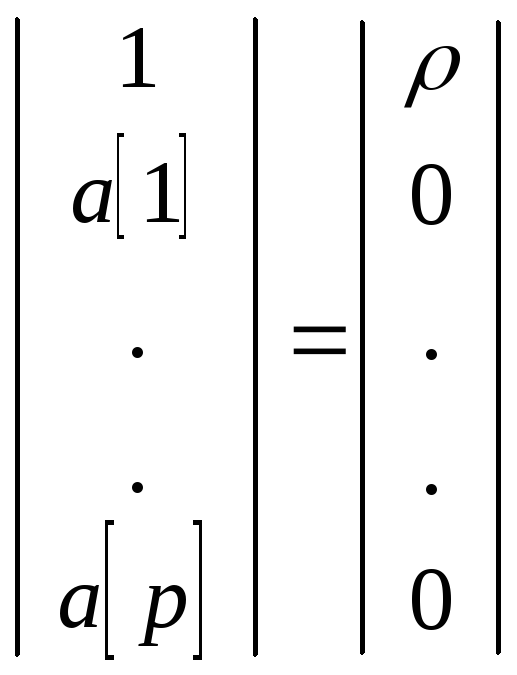. (2.13)

Таким образом, если задана автокорреляционная последовательность для , то АР-параметры можно найти в результате решения последнего матричного соотношения (называемого нормальными уравнениями Юла-Уалкера).

Наиболее очевидным подходом к авторегрессионному оцениванию является решение нормальных уравнений Юла-Уалкера, в которые вместо значений неизвестной автокорреляционной функции подставляем их оценки.

Методы оценивания коэффициентов отражения

Рекурсивное решение уравнений Юла-Уалкера методом Левинсона связывает АР-параметры порядка p c параметрами порядка p-1 выражением

, где n=1,2,..p-1. (2.14)

Коэффициент отражения определяется по известным значениям автокорреляционной функции

, (2.15)

, где. (2.16)

Из всех величин только непосредственно зависит от автокорреляционной функции. В разное время предлагалось несколько различных процедур оценки коэффициента отражения, рассмотрим некоторые из них.