3. Статич звено второго порядка
Статич
звено второго порядка. Выходная
и вход величины связ линейным дифф
ур-нием второго порядка:
a2d2y/dτ2+a1dy/dτ+a0y=b0x,
K=b0/a0,
T2=a2/a0,
2ζT=a1/a0,
K,T,ζ-коэфф усилений, постоян времени,
коэфф демпфирования. T2
d2y/dτ2+2ζTdy/dτ+у=Кх.
Различ звенья: ζ≥1-апериодич,0<ζ<1 –
колебат; ζ=0 – консерватив. Если ζ=1, то
демпфирование назыв критическим. Ур-ние
колебат звена: 1/w02
d2y/dτ2+2ζ/w0dy/dτ+у=Кх,w0-частота
свобод колебаний недемпфирован системы.
При 0≤ζ≤1 выход сигнал будет соверш
затухающ колеб (слабо демпфирован
система). При ζ=0 выход сигнал представ
собой незатух колеб (недемпфир). ζ>1 –
без колебат процесса тем медленнее,
чем больше ζ (сильно демпфир).Придаточ
ф-ция: W(s)=K/(T2s2+2ζTs+1).
Характерист ур-ние:T2s2+2ζTs+1=0,
его корни: s1,2=(-ζ±
)/T.
Переход
хар-ка:
h(τ)=L-1{W(s)*1/s}=
L-1{(K/(T2s2+2ζTs+1))*1/s}.
1) ζ>1 s1=-α1,
s2=-α2:
h(τ)=L-1{(K/(T2
(s+
α1)(s+
α2))*1/s}-апериодич
процесс. 2) ζ=1 s1=s2=-1/Т=-α:
h(τ)=L-1[K/(T2
(s+
α)2]-апериодич
процесс. 3) 0<ζ<1 s1,2=-
ζ /Т±j
=-α±jβ:
h(τ)=L-1{[K/(T2
(s+
α)2+β2)]*1/s}-колебат
процесс.
4)ζ=1 s1,2=±j1/Т: h(τ)=L-1{[K/(T2s2+1)]*1/s}=К(1-cosτ/T)*1(τ)=K(1-cosw0τ)*1(τ) –незатух колеб.
Частотные
хар-ки:
АФЧХ: W(jw)=K/(T2(jw)2+2ζT(jw)+1)=
.
АЧХ:
A(w)=│W(jw)│=
.ФЧХ:
φ(w)=-arctg
(2Tζw/(1-T2w2)),
w≤wc=1/T;
φ(w)=-π-arctg
(2Tζw/(1-T2w2)),
w>wc=1/T.
Частот
передаточ
ф-ция:
W(jw)=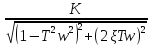
exp[-j
arctg (2Tζw/(1-T2w2))].
ЛАЧХ:
L(w)=20lgK-20lg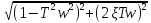
.
Lнча=20lgK-20lg1=20lgK
–низкочастот
(Tw<<1). Высокочастот:
Lвча=20lg(K/T2)-40lgw.
4. Звено запаздывания
Ззвено, которое не измен вид входного сигнала, а лишь задержив во времени, т.е., если в момент τ=0 вход величина начинает измен по опред з-ну, то спустя время запазд τзап по такому же з-ну начнет меняться и выход величина (время транспорт запазд). Если 0<τ<τзап, то y(τ)=0, выход величина неизменна, если τ>τзап, то выход величина в момент времени τ будет такой же, какой была вход величина в момент времени τ-τзап: y(τ)=х(τ-τзап).
АФХЧ:
На входе: x(τ)=Axeiwτ.
Спустя время τзап
на выходе: у(τ)=Aуeiw(τ-τзап).
Частот передат ф-ция: W(jw)=y(τ)/x(τ)=(Ay/Ax)*e
–iwτзап.
Передат ф-ция звена запазд: W(s)=e
–sτзап.
АЧХ: A(w)=(Ay/Ax)(w)=1,
ФЧХ: φ(w)=-τзапw.
Звено равномерно пропуск все сдвиги
фаз, пропорц времени τзап.
ЛАЧХ: L(w)=20lg1=0. 
5. Идеальное инегрир звено.
Звено
интегрир, если скорость изменения его
выходн величины пропорц входной
величине: Tady/dτ=x,
Tа-
постоянная времени интегрир.
.
.
Передат
ф-ция:
W(s)=L(y)/L(x)=K*1/s=1/(Tas).
Переход
ф-ция:
h(τ)=L-1[W(s)*1/s]=(1/Ta)*L-1(1/s2)=(1/Ta)*τ.
Частотная передат ф-ция: W(jw)=1/(Tawj)=-j/(Taw). АЧХ: A(w)=1/(Taw). ФЧХ: φ(w)=arctg(-∞)=-π/2. Частот передат ф-ция в показат форме: W(jw)=1/(Taw)*е-jπ/2. ЛАЧХ: L(w)=20lgA(w)=2-lg1/Ta-20lgw.
Реальное интегрир звено. TTad2y/dτ2+Tady/dτ=x. Придаточ ф-ция: W(s)=1/(Tas(Ts+1)). Реальн интегрир звено можно рассматрив как последоват соедин идеальн интегрир и статич звена первого порядка.