8. Расчёт переходного процесса при произвольном воздействии с помощью интеграла Дюамеля

Интеграл Дюамеля, одна из форм записи которого имеет вид

,

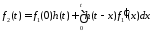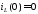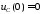используется для определения реакции цепи на воздействие произвольной формы, при отсутствии запаса энергии в цепи в момент коммутации (если все и). Здесь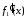есть производная воздействия по времени при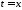,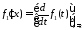. Переходная характеристика цепи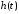 - описывает свойства пассивной цепи, и определяется через передаточную функцию .

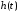
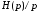Возьмем для примера ту же цепь (раздел 6, рис.6) при воздействии 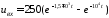и при нулевых начальных условиях. Требуется вычислить интеграл

.

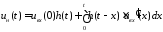Для этого определим: 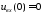и

.

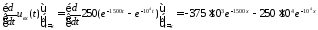Переходную характеристику 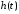вычислим, используя процедуру обратного преобразования Лапласа (invlaplace). При ручных вычислениях следует не забывать, что переменная интегрирования х, и следовательно составляющие подынтегрального выражения, содержащие время t выносятся за знак интеграла как постоянные. Полный расчёт приведён в приложении 10.

В рассмотренном примере воздействие 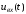функция непрерывная, (рис.9) и её производная не имеет разрывов. Сложней, если воздействие представляет собой функцию типа, показанной на рисунке 10, где производная имеет разрывы и принимает бесконечные значения. В этом случае воздействие следует представить наложением отдельных составляющих, каждая из которых во временных пределах задания будет непрерывной. В конкретном случае составляющих будет три. Первая составляющая, это прямая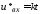, гдеk тангенс угла наклона. 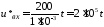В. Соответственно производная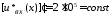. 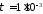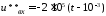Вторая прямая отличается от первой только знаком и сдвигом по временной оси нас.В.

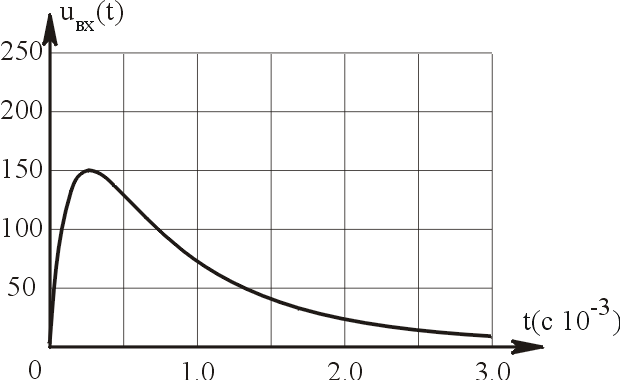
Рис.9

Соответствующее значение (с минусом) будет у производной. Третья составляющая, - это отрицательный скачок напряжения, сдвинутый по времени на 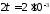с.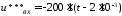В. Производная равна нулю.

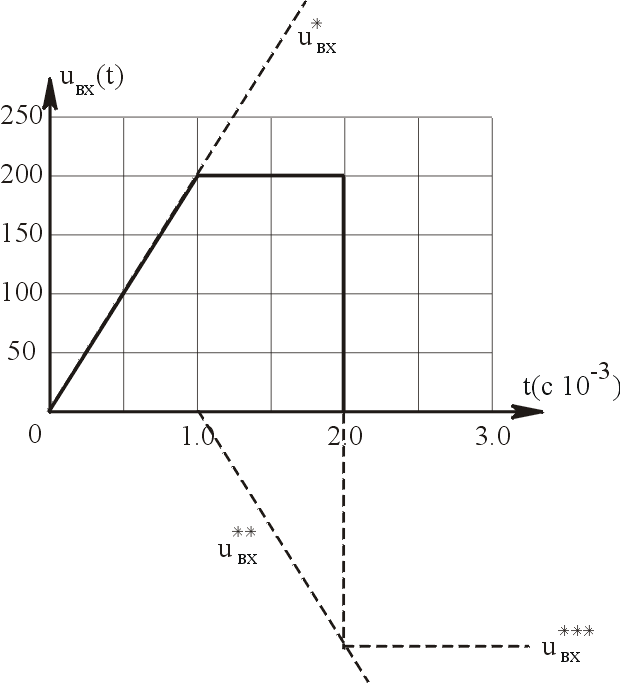
Рис.10

Из рисунка видно, что наложение трёх составляющих даёт исходное напряжение 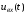, причём у всех составляющих производные не имеют разрывов в пределах задания. В соответствии с принципом наложения, полную реакцию цепи можно вычислить наложением реакций от отдельных воздействий.

9. Анализ свойств цепи по расположению полюсов на комплексной плоскости.

Полное решение для переходного процесса в линейной цепи есть сумма

.

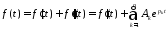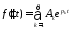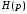Свободная составляющая переходного процесса определяется только свойствами цепи и напрямую связана с расположением корней характеристического уравнения (полюсов) на комплексной плоскости. Расположение полюсов позволяет оценить характер переходного процесса, а именно колебательный или экспоненциальный, частоту собственных колебаний и максимальное время практического завершения процесса.

Задания на курсовую работу содержат только пассивные электрические цепи, что исключает наличие полюсов в правой полуплоскости и, следовательно, неустойчивый характер переходного процесса. Не может быть и пар чисто мнимых полюсов, т.к. все варианты содержат резистивные элементы, и это исключает появление незатухающих колебаний. Возможны случаи:

а) когда полюса расположены в левой полуплоскости и вещественны 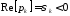. Им соответствуют экспоненциальные, убывающие со временем составляющие решения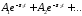. Длительность переходного процесса определяется минимальным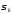. С абсолютной достоверностью процесс заканчивается за время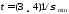. Практически переходный процесс может закончиться раньше (причём значительно), т.к. коэффициент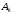приможет оказаться существенно меньше остальных коэффициентов.

б) полюса комплексно-сопряжённые 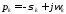и 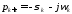. Им соответствуют колебательные экспоненциально убывающие составляющие решения

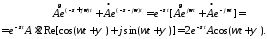
Время завершения переходного процесса определяется, как и в предыдущем случае, минимальным значением 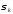, а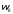 - есть частота собственных колебаний с периодом .

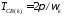в) полюс расположен в начале координат 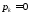. Решение содержит постоянную составляющую.

В примере для цепи (рис.1,раздел 1) определена передаточная функция

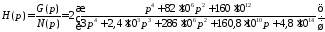
Корни полинома

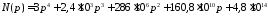
определены выше в разделе 1. Четыре полюса: 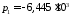, пара комплексно – сопряжённых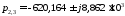и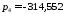располагаются на комплексной плоскости следующим образом (рис.11).

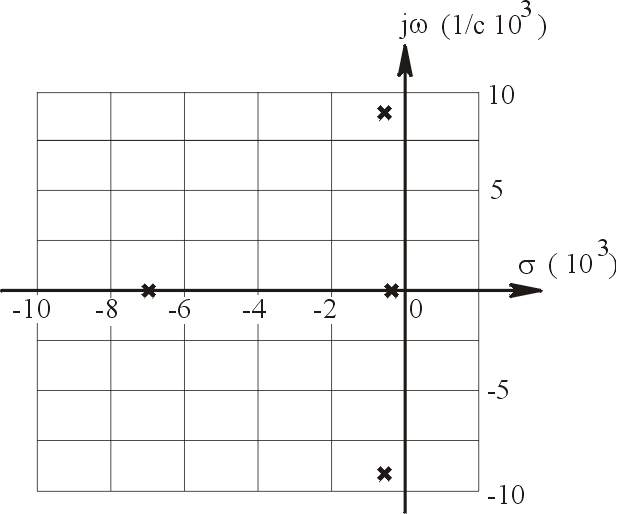
Рис.11

Наименьшее по абсолютной величине значение по вещественной оси имеет последний полюс 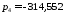. Он определяет максимально возможную длительность переходного процесса 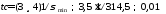. График переходного процесса (раздел 6) свидетельствует о том, что переходный процесс при частоте воздействия 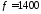Гц практически завершён за время .

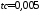Частота свободных колебаний 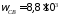1/с (или приблизительно 1400Гц), совпадает с частотой воздействия и поэтому не проявляется в кривой выходного напряжения. В ином случае частота (частоты) свободных колебаний наложились бы на частоту воздействия. В разделе 8 (интеграл Дюамеля) воздействие есть непериодическая функция. В реакции на это воздействие (см. график решения) отчётливо проявляется частота собственных колебаний с периодом приблизительно 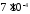с, т.е. 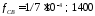с частотойГц.