Методические указания к выполнению лабораторной работы № 2.1.7
ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ МЕТАЛЛОВ
Теоретические положения
Электрическим током называют упорядоченное движение заряженных частиц или макроскопических тел. Различают два вида электрического тока: ток проводимости и конвекционный. Электрическим током проводимости называют упорядоченное движение в веществе или вакууме свободных заряженных частиц – носителей тока.
Конвекционным электрическим током называют ток, возникающий при движении в пространстве заряженного макроскопического тела.
Для возникновения тока проводимости в веществе необходимо наличие в нем свободных носителей тока, а также существование внутри тела электрического поля. За направлением электрического тока условно принимают направление движения носителей положительных зарядов, то направление электрического тока считается противоположным направлению их движения.
В металлах носителями тока являются отрицательно заряженные электроны, поэтому направление тока в металлах противоположно направлению движения электронов.
Количественной характеристикой электрического тока служит сила тока – скалярная физическая величина, характеризующая скорость переноса электрического заряда через рассматриваемую поверхность:
Здесь
- заряд, который переносится через
рассматриваемую поверхность за время
.
Ток, не изменяющийся с течением времени, называют постоянным. Сила постоянного тока
.
В СИ единицей силы
тока является ампер (А). Электрический
ток может быть распределен по сечению
проводника, через который он проходит,
неравномерно. Распределение тока по
сечению проводника характеризуют с
помощью вектора плотности тока
.
Этот вектор численно равен отношению
силы тока
,
проходящего через расположенную в
данной точке перпендикулярную к
направлению движения носителей тока
физически бесконечно малую поверхность,
к площади этой поверхности
:
.
Направление вектора
совпадает с направлением вектора
скорости упорядоченного движения
носителей положительных зарядов. Зная
вектор плотности тока в каждой точке
пространства, можно найти силу тока
,
проходящего через произвольную
поверхность площадью
,
как поток через эту поверхность вектора
плотности тока:
.
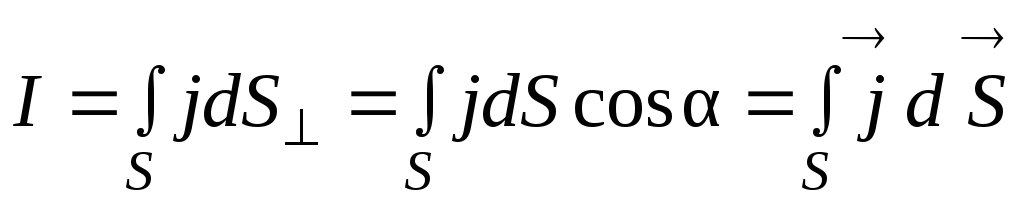Здесь 
,
где
- единичный вектор нормали к поверхности
площадью
;
- угол между
векторами
и
.
Если постоянный электрический ток течет вдоль однородного цилиндрического металлического проводника, то плотность тока одинакова по всему поперечному сечению проводника; в этом случае
.
В СИ единица
плотности тока – ампер на квадратный
метр
.
Выделим мысленно
в металлическом проводнике, по которому
течет ток, физически бесконечно малый
объем. Если концентрация носителей тока
в этом объеме равна
.
каждый носитель имеет заряд
,
средняя скорость упорядоченного движения
носителей (скорость дрейфа) -
,
то за время
через поверхность площадью
будет перенесен заряд
.
Тогда для плотности тока получим выражение
|
(1) |
.
Немецкий физик Г.
Ом экспериментально установил, что сила
тока
,
текущего по однородному металлическому
проводнику пропорциональна приложенному
напряжению
(в случае однородного проводника
напряжение
совпадает с разностью потенциалов
):
|
(2) |
,
где
- электрическое сопротивление проводника,
Ом.
Сопротивление зависит от формы и размеров проводника, также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника
|
(3) |
,
где
– удельное электрическое сопротивление,
;
– длина проводника,
м;
S
– площадь поперечного сечения проводника,
Величина
называется электрической проводимостью
проводника. В СИ единица электрической
проводимости – сименс (См).
Величина
называется удельной электрической
проводимостью.
.
Перемещение зарядов
в проводнике происходит под действием
электрического поля. В изотропном
проводнике упорядоченное движение
носителей тока происходит вдоль линии
напряженности электрического поля.
Поэтому направления векторов
и
совпадают.
Выделим мысленно
в изотропном металлическом проводнике
элементарный цилиндр с образующими,
параллельными векторам
и
.
Высоту цилиндра обозначим
,
а площадь основания –
.
Через поперечное сечение цилиндра течет
ток
.
Напряжение, приложенное к цилиндру,
равно
,
а его сопротивление согласно формуле
(3) –
.
Подставив эти значения в уравнение (2),
получим
; 
.
Или в векторной форме
|
(4) |
.Эта формула выражает закон Ома в дифференциальной форме.
Уравнения (2) и (3) позволяют рассчитать силу тока и сопротивление в том случае, когда проводник имеет постоянное сечение. Выражение (4) пригодно для решения и более сложных задач по расчетам тока.
Объяснение механизма электрической проводимости металлов дано в классической теории Друде – Лоренца. В рамках этой теории электроны проводимости рассматриваются как электронный газ, обладающий свойствами одноатомного идеального газа. Оценку средней скорости теплового движения электронов можно произвести по формуле известной из кинетической теории идеальных газов:
,
где
– постоянная Больцмана. Дж/К;
– термодинамическая
температура, К;
– масса электрона,
кг;
В отсутствие электрического поля электроны проводимости хаотически движутся и сталкиваются с ионами металла, которые совершают беспорядочные колебания около положений равновесия – узлов кристаллической решетки.
Электрический ток в металле возникает под действием электрического поля, которое приводит к появлению упорядоченного движения электронов. Между двумя последовательными соударениями электроны движутся под действием поля с ускорением и приобретают определенную энергию. Эта энергия передается ионам металла при соударениях и превращается в энергию беспорядочных колебаний, то есть в тепловую энергию. Поэтому металлы нагреваются при прохождении тока.
В классической
теории предполагается, что при соударениях
с ионами электроны полностью теряют
скорость упорядоченного движения. Пусть
в металлическом проводнике существует
однородное электрическое поле
напряженностью
.
Под действием этого поля электроны
будут двигаться с ускорением, равным
,
и к концу пробега скорость дрейфа
достигнет в среднем значения
,
где
– среднее время между двумя последовательными
соударениями электрона с ионами
кристаллической решетки, с.
Скорость
дрейфа
изменяется за время пробега линейно.
Поэтому ее среднее значение за пробег
равно половине максимального:
.
Подставив это выражение в формулу (I), получим
,
где
.
Удельное сопротивление проводника тем меньше, чем больше концентрация свободных электронов и среднее время свободного пробега. Если бы электроны не сталкивались с ионами решетки, то время свободного пробега, а следовательно, и удельная проводимость были бы бесконечно велики.
Таким образом, согласно классическим представлениям электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами кристаллической решетки.