
Microsoft Word - Физика атома и ФФТ_3
.pdfФедеральное агентство морского и речного транспорта |
|
|
УДК 534 (075.8) |
Федеральное государственное образовательное учреждение |
|
высшего профессионального образования |
Воробьёв, Ю. Д. Физика атома и физика твёрдого тела. [Текст] : учеб. |
«Морской государственный университет им. адм. Г. И. Невельского» |
пособие / Ю. Д. Воробьёв. – Владивосток : Мор. гос. ун-т, 2010. – 120 с. |
|
Учебное пособие написано в соответствии с действующей программой |
|
курса физики для инженерно-технических специальностей высших ученых |
|
заведений. |
|
В пособие включены краткая теория и лабораторные работы из двух |
Ю. Д. Воробьёв |
раздела программы - физики атома и физики твёрдого тела. В конце каждого |
|
раздела приведены описания используемых лабораторных комплексов и |
|
приборов. |
Ф И З И К А А Т О М А |
|
И |
Рецензент |
Ф И З И К А Т В Ё Р Д О Г О Т Е Л А |
|
|
В. Э. Осуховский, д-р физ.-мат. |
Учебное пособие |
наук, профессор, заведующий |
|
кафедрой физики и ОТД Фи- |
Рекомендовано научно-методическим советом |
лиала ВУНЦ ВМФ «ВМА» |
морского государственного университета |
|
в качестве учебного пособия для курсантов и студентов |
|
всех специальностей |
|
© Воробьев Ю. Д., 2010 © Морской государственный университет
им. адм. Г. И. Невельского, 2010
Владивосток
2010
1 |
2 |

ОГЛАВЛЕНИЕ ФИЗИКА АТОМА
1. |
СПЕКТР АТОМА ВОДОРОДА |
5 |
2. |
ПОСТУЛАТЫ БОРА |
6 |
3. |
ОПЫТ ФРАНКА И ГЕРЦА |
7 |
4. |
ТЕОРИЯ СПЕКТРА АТОМА ВОДОРОДА ПО БОРУ |
10 |
|
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ I |
|
1. |
ЛАБОРАТОРНАЯ РАБОТА № 3.49. ОПЫТ ФРАНКА И ГЕРЦА |
13 |
2. |
ЛАБОРАТОРНАЯ РАБОТА № 3.17. СПЕКТРАЛЬНЫЙ АНАЛИЗ |
15 |
3. |
ЛАБОРАТОРНАЯ РАБОТА 3.18. ИЗУЧЕНИЕ СПЕКТРА АТОМА |
|
ВОДОРОДА |
25 |
|
4. |
ЛАБОРАТОРНАЯ РАБОТА № 3.19. ИЗУЧЕНИЕ СПЕКТРА |
|
ИЗЛУЧЕНИЯ АТОМОВ |
27 |
|
5. |
ЛАБОРАТОРНАЯ РАБОТА № 3.20М. МОДЕЛИРОВАНИЕ СПЕКТРА |
|
АТОМА ВОДОРОДА |
30 |
|
ПРИЛОЖЕНИЕ №1. СПЕКТРЫ НЕКОТОРЫХ ЭЛЕМЕНТОВ |
32 |
|
ПРИЛОЖЕНИЕ № 2. МОДУЛЬНЫЙ УЧЕБНЫЙ КОМПЛЕКС МУК-ОК |
|
|
«КВАНТОВАЯ ОПТИКА» |
33 |
|
ПРИЛОЖЕНИЕ № 3. МОНОХРОМАТОР УМ-2 |
34 |
|
|
ФИЗИКА ТВЁРДОГО ТЕЛА |
|
1. |
ЭЛЕКТРОПРОВОЛНОСТЬ ТВЁРДЫХ ТЕЛ |
38 |
2. |
КОНТАКТ ДВУХ МЕТАЛЛОВ ПО ЗОННОЙ ТЕОРИИ |
47 |
|
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ II |
|
1. |
ЛАБОРАТОРНАЯ РАБОТА № 3. 10М. ТЕРМОМЕТРЕТИЯ |
52 |
2. |
ЛАБОРАТОРНАЯ РАБОТА № 3. 11М. ИЗУЧЕНИЕ ТЕМПЕРАТУРНОЙ |
|
ЗАВИСИМОСТИ ЭЛЕКТРОСОПРОТИВЛЕНИЯ МЕТАЛЛА И |
|
|
ПОЛУПРОВОДНИКОВ |
61 |
|
3. ЛАБОРАТОРНАЯ РАБОТА № 3.03. ФОТОПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ 67
4. ЛАБОРАТОРНАЯ РАБОТА № 3. 11. ИЗУЧЕНИЕ ТЕМПЕРАТУРНОЙ
ЗАВИСИМОСТИ ЭЛЕКТРОСОПРОТИВЛЕНИЯ ПОЛУПРОВОДНИКА |
74 |
5. ЛАБОРАТОРНАЯ РАБОТА № 3.12. ИЗУЧЕНИЕ СПЕКТРАЛЬНОЙ |
|
ХАРАКТЕРИСТИКИ ФОТОРЕЗИСТОРА |
76 |
6. ЛАБОРАТОРНАЯ РАБОТА № 46 А. ТЕРМОЭЛЕКТРОННАЯ |
|
ЭМИССИЯ И КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ |
79 |
7. ЛАБОРАТОРНАЯ РАБОТА № 3.47. РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ |
|
ПО СКОРОСТЯМ ПРИ ТЕРМОЭЛЕКТРОННОЙ ЭМИССИИ |
86 |
ПРИЛОЖЕНИЕ А |
91 |
ПРИЛОЖЕНИЕ Б |
96 |
ПРИЛОЖЕНИЕ В |
100 |
3 |
4 |
ФИЗИКА АТОМА
1. Спектр атома водорода
Экспериментальное исследование спектров излучения разрежённых газов (отдельных атомов), т.е. газов для которых взаимодействием между атомами можно пренебречь, показали, что характерный линейчатый спектр каждого элемента представляет собой серии линий, положение которых может быть описано простыми эмпирическими формулами. Так, например, положение линий излучения атома водорода в видимой области спектра для длин волн описываются формулой Бальмера:
|
|
|
|
|
|
|
1 l = R |
¢ |
( |
|
|
2 |
-1 n |
2 |
) |
|
|
|||
|
|
|
|
|
|
|
|
1 2 |
|
|
|
, |
(1.1) |
|||||||
|
|
|
|
|
|
|
æ |
|
c ö |
|
|
|
|
|
|
|
|
|
|
|
или используя соотношение çn = |
|
÷ |
|
для частот |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
è |
|
l ø |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = R 1 22 -1 n 2 |
|
|
|
n = 3, 4, 5,….. |
(1.1а) |
||||||||||
где R |
¢ |
= 1,1∙10 |
7 |
-1 |
|
|
¢ |
|
|
|
|
15 |
|
-1 |
- постоянная Ридберга |
|||||
|
м |
|
, R = R c =3,29∙10 |
|
c |
|||||||||||||||
Позднее, в ультрафиолетовой области была обнаружена: |
|
|||||||||||||||||||
серия Лаймана |
|
|
n = R |
( |
-1 n 2 |
|
) |
|
n |
= 2, 3, 4, 5,… |
(1.2) |
|||||||||
|
|
|
1 12 |
|
|
|
||||||||||||||
и в инфракрасной области |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
||||||
серия Пашена: |
|
|
n = R |
( |
-1 n 2 |
|
|
|
n = 4, 5, 6,… |
(1.3) |
||||||||||
|
|
( |
1 32 |
) |
|
|
|
|||||||||||||
серия Брэкета: |
|
|
|
|
-1 n 2 |
|
|
|
n = 5, 6, 7,… |
(1.4) |
||||||||||
|
|
n = R 1 42 |
) |
|
|
|
||||||||||||||
серия Пфунда: |
|
|
n = R |
( |
-1 n 2 |
|
|
|
n = 6, 7, 10,… |
(1.5) |
||||||||||
|
|
|
1 52 |
) |
|
|
|
|||||||||||||
серия Хемфри: |
|
|
n = R |
( |
-1 n 2 |
|
|
|
n = 7, 10, 9,… |
(1.6) |
||||||||||
|
|
|
1 62 |
|
|
|
|
|||||||||||||
Все эти серии могут быть описаны обобщенной формулой Бальмера:
æ |
1 |
|
|
1 ö |
|
|||
n = R ç |
|
|
- |
|
|
|
÷ |
(1.7) |
|
2 |
n |
2 |
|||||
èm |
|
|
|
ø |
|
|||
где m = 1,2,3,4,5,6 определяет серию, а n = m +1, m +2, определяет отдельные линии этой серии. С увеличением n линии серии сближаются; значение n = ∞ определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр. Аналогичные серии были выделены в линейчатых спектрах других атомов.
2. Постулаты Бора
Для объяснения закономерностей в линейчатых спектрах Бор объединил планетарную модель атома Резерфорда с гипотезой Планка о квантовой природе света. Теория атома Бора основывается на двух постулатах:
(1) Первый постулат (постулат стационарных состояний): существуют стационарные (не изменяющиеся со временем) состояния атома, находясь в которых он не излучает энергии.
В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантованные значения момента импульса, удовлетворяющие условию
mev ×rn = nh ( n = 1, 2, 3, ) (2.1)
где me — масса электрона, и v — его скорость на n -й орбите радиуса rn , h = h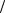 2p - постоянная Планка.
2p - постоянная Планка.
Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Каждое стационарное состояние характеризуется определённым (дискретным) значением энергии. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.
(2) Второй постулат (правило частот): при переходе атома из одного состояния в другое испускается или поглощается один фотон с энергией
hn = En - Em |
(2.2) |
равной разности энергий соответствующих стационарных состояний. Излучение фотона происходит при переходе атома из состояния с большей
энергией в состояние с меньшей энергией ( Em < En ), т.е. при переходе электрона с орбиты более удалённой от ядра на ближнюю к ядру орбиту.
Рис. 2.1.
5 |
6 |
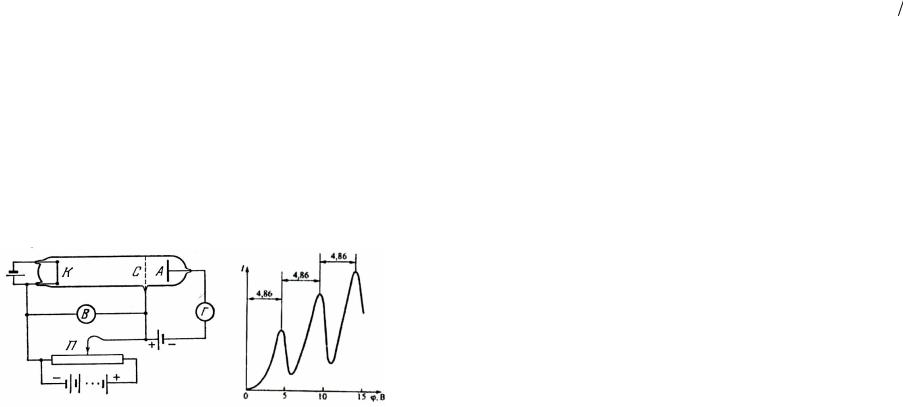
Поглощение фотона сопровождается переходом атома в состояние с большей энергией ( Em > En ), т.е. переходом электрона на более удалённую от
ядра орбиту.
Набор всевозможных дискретных частот квантовых переходов:
n = |
En - Em |
= |
DE |
(1.8) |
|
h |
|||
|
h |
|
||
определяет линейчатый спектр атомов (см. Приложение №1)
3. Опыт Франка и Герца
Одним из простых опытов, подтверждающих существование дискретных уровней энергии атомов, является эксперимент, известный под названием опыта Франка и Герца (1914г.). В опытах Франка и Герца было экспериментально доказано существование в атомах стационарных состоянии.
Схема опыта изображена на рис.3.1а. В трубке заполненной парами ртути под небольшим давлением (~ 1мм.рт.ст.) имелись три электрода: катод К, сетка С и коллектор А. Электроны, эмитированные катодом, вследствие термоэлектронной эмиссии разгоняются в области между катодом и сеткой разностью потенциалов U и бомбардируют атомы ртути. Эту разность потенциалов можно изменять с помощью потенциометра П. Между сеткой и анодом создавалось слабое электрическое поле ~ 0.5 В, тормозившее движение электронов к аноду.
Рис. 3.1.
Исследовалась зависимость силы тока I цепи катода от напряжения U между катодом и сеткой. Из рис. 3.1б видно, что сила тока вначале монотонно возрастает, достигает максимума при 4,86 эВ, после чего ток в установке резко
уменьшается. При дальнейшим увеличением U ток снова начинает расти до максимума. Эти максимумы регулярно наблюдаются с периодом 4,86 эВ. Такое поведение тока связано с тем, что первое возбужденное состояние атома ртути имеет энергию E = eU = 4,86 эВ.
Если бы в трубке был вакуум, то график зависимости I от U КС |
имел вид |
гладкой кривой. Действительно, при увеличении U КС увеличивается работа |
|
ускоряющего электрического поля над электронами eU КС = mv 2 |
2 . Элек- |
троны приобретают на промежутке катод-сетка всё большую кинетическую энергию и, попадая после этого в область тормозящего поля, все достигают
коллектора. Поэтому сила в цепи растет с увеличением U КС .
При наличии же в трубке паров ртути (или другого газа) характер зависимости резко меняется (рис. 2). Плавное возрастание силы тока с увеличением
U КС сменяется при определенных значениях U КС резкими падениями, после которых опять наблюдается плавный рост.
Такой ход зависимости I объясняется тем, что атомы ртути могут
получать энергию при столкновении с электронами только определёнными порциями (квантами). Причем наименьшая порция энергии, которую может поглотить атом, находящийся в самом низком (основном) энергетическом со-
стоянии E1 , равна разности между энергией первого возбужденного состояния атома E2 и энергией основного состояния:
DE = E2 - E1 .
Пока разность потенциалов U КС мала, кинетическая энергия электрона
при его ускорении в промежутке катод-сетка остаётся меньше чем DE . Атом не может принять энергию от электрона при столкновении и перейти в возбуждённое состояние. Взаимодействие электрона с атомом носит характер упругого удара. Причем из-за огромной разницы в массах электрона и атома, элек-
трон после удара не теряет своей скорости. По мере увеличения U КС кинетическая энергия электрона растёт и при определённом значении U КС =U ВОЗБ
становится равной DE (строго говоря, чуть большей). При такой разности потенциалов характер взаимодействия атома с электроном резко меняется. Атом газа поглощает энергию электрона и переходит в возбуждённое энергетическое состояние. А электрон, потеряв при ударе, который теперь имеет характер неупругого, почти всю свою кинетическую энергию, практически останавливается (приобретает скорость равную скорости атома после удара). Это происходит около сетки, т.к. именно здесь кинетическая энергия электрона достигает наибольшего значения. Практически остановившийся электрон уже не имеет достаточной энергии, чтобы, попав в тормозящее поле, долететь до
7 |
8 |

коллектора. Следовательно, сила тока I при разности потенциалов U КС =U ВОЗБ падает. Разность потенциалов U ВОЗБ , которая необходима для
того, чтобы кинетическая энергия электрона достигла величины DE , называется потенциалом возбуждения.
При дальнейшем увеличении U КС сила тока коллектора опять возрастает:
электроны, испытавшие неупругие соударения, успевают набрать энергию, достаточную для преодоления задерживающего поля. При этом область неупругого удара всё дальше отодвигается от сетки, приближаясь к катоду.
Следующее падение силы тока коллектора происходит, когда часть электронов неупруго сталкиваются с атомами газа два раза на пути к сетке: первый раз посередине промежутка катод – сетка, второй – около сетки, и т.д. Таким
образом, на графике зависимости I от U КС имеется несколько максимумов и минимумов, отстоящих друг от друга на равные расстояния U ВОЗБ .
В возбуждённом состоянии атомы обычно находятся очень короткое время ~10-8с. После этого атом возвращается в основное энергетическое состояние, испуская излишек энергии часто в виде электромагнитного излучения (кванта света, фотона). Причём
hw = DE = eU ВОЗБ ,
где |
hw - энергия фотона при циклической частоте световой |
волны |
||
w = 2p |
c |
; h = 1, 054887 ×10-34 Дж×с - постоянная Планка с чертой; с |
= 3×108 |
|
l |
||||
|
|
|
||
м/с – скорость света в вакууме; l - длина волны света, испущенного атомом; e = 1,602×10-19 Кл – элементарный заряд (заряд электрона).
Если предположения Бора верны, то атомы ртути, бомбардируемые электронами с энергией 4,86 эВ, должны являться источником ультрафиолетового излучения с l » 255 нм. Именно такое излучение и было обнаружено в эксперименте. Это говорит о том, что в атоме действительно существуют стацио-
нарные состояния (подтверждение первого постулата Бора). Возбуждённые атомы ртути, переходя в основное состояние, излучают кванты света с длиной
волны l = hc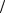 DE =255нм (подтверждение второго постулата Бора).
DE =255нм (подтверждение второго постулата Бора).
Таким образом, опыты Франка и Герца экспериментально подтвердили не только первый, но второй постулат Бора.
Значения потенциалов возбуждения для различных газов приведены в таблице 1:
|
|
|
|
|
|
|
|
Таблица 1 |
||
|
|
|
|
|
|
|
|
|
|
|
Газ |
H2 |
He |
Ne |
Ar |
Kr |
Xe |
Hg |
|
Cs |
|
UВОЗБ, В |
11,2 |
20,9 |
16,6 |
11,6 |
10,0 |
8,5 |
4,9 |
|
1,4 |
|
4. Теория спектра атома водорода по Бору
В 1913 году Бор, используя резерфордовскую модель атома, гипотезу Планка и предложенные им постулаты, разработал теорию спектра водородоподобного атома – атома содержащего ядро с зарядом Ze и один электрон,
который движется вокруг ядра (например, ионы He + Z = 1 такая система соответствует атому водорода.
При рассмотрение движения электрона в водородоподобной системе, ограничимся круговыми стационарными орбитами. Согласно первому постулату Бора возможны только такие орбиты, для которых момент импульса электрона
на этой орбите p = mev ×r удовлетворяет условию:
mev ×r = nh ( n = 1, 2, 3, ). (4.1)
Уравнение движения электрона следует из второго закона Ньютона F = meaц
где F = |
Ze ×e |
кулоновская сила, |
m |
|
- масса электрона, |
a |
|
= |
v 2 |
- цен- |
|||
4pe0 ×r 2 |
e |
ц |
r |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
тросремительное ускорение и имеет вид: |
|
|
|
|
|
|
|
|
|||||
|
|
|
Ze ×e |
= |
mev 2 |
|
|
(4.2) |
|
||||
|
|
|
4pe0 ×r 2 |
|
|
|
|||||||
|
|
|
|
|
r |
|
|
|
|
|
|||
Выразив из (4.1) линейную скорость электрона v и подставив в (4.2) получим выражение для радиусов разрешённых орбит:
r |
= |
h2 × 4pe0 |
×n 2 |
( n = 1, 2, 3, ) .(4.3) |
n |
|
me Ze 2 |
|
|
Радиус первой орбиты водородоподобного атома Z = 1 при n = 1 называется первым боровским радиусом:
a = r1 = h2 × 4pe0 = 5,28∙10-11 м = 0.529Å. mee 2
Отметим, что боровский радиус a совпадает со значением газокинетических размеров атомов. Так как радиусы стационарных орбит измерить невозможно, необходимо вывести из теории такие величины которые поддаются экспериментальному определению. Такой величиной является энергия, излучаемая или поглощаемая атомами водорода.
Внутренняя энергия атома слагается из кинетической энергии электрона (считаем ядро неподвижным) и энергии взаимодействия электрона с ядром
E = |
m v 2 |
- |
Ze 2 |
|
e |
|
. |
||
2 |
|
|||
|
|
4pe r |
||
|
|
|
0 |
|
9 |
10 |
Из (4.2) следует |
|
|
|
|
|
|
|
|
|
|
||
mev 2 |
1 |
|
Ze 2 |
|
|
|
|
|
||||
|
|
|
= |
|
|
|
|
. |
|
|
|
|
2 |
|
2 |
4pe r |
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Следовательно |
|
|
|
|
|
|
|
|
|
|
||
E = |
|
Ze 2 |
|
- |
Ze 2 |
= - |
|
Ze 2 |
||||
2 |
×4pe r |
4pe r |
2 |
×4pe r |
||||||||
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
Подставив сюда выражение для радиуса стационарных орбит (4.3) найдём разрешённые значения внутренней энергии атома:
|
m e e 4 |
1 |
|
|
|
En = -Z |
|
× |
|
× ( n |
= 1, 2, 3,….∞) (4.4) |
8h 2e02 |
n 2 |
||||
где знак минус означает, что электрон находится в связанном состоянии. Схема энергетических уровней определяемой формулой (4.4) приведена на
рис.7.
Целое число n , определяющее энергетические уровни атома, называется главным квантовым числом. Энергетический уровень с n = 1 называется основным (нормальным) уровнем, а соответствующее ему состояние атома назы-
вается основным (нормальным) состоянием. Уровни с n >1 и соответствую-
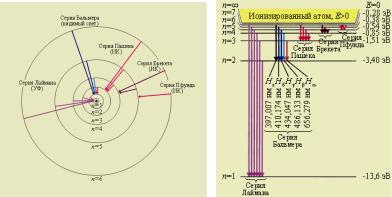
щие им состояния называются возбуждёнными. Придавая n целочисленные значения, получаем для атома водорода энергетические уровни, или линейчатый спектр, представленный на рис. 7.
Рис. 7
Минимальная энергия атома водорода: Е1 = -13,55 эВ.
Максимальная энергия электрона E∞ = 0 при n = ∞ называется энергией ионизации атома (при Е = E∞ происходит отрыв электрона от атома), то есть
Eион = En =¥ - En =1 или
|
me 4 |
¢ |
|
Eион = |
|
|
= R hc |
2 |
2 |
||
|
8e h |
|
|
|
0 |
|
|
Переход из стационарного состояния n в стационарное состояние m , согласно второму постулату Бора, сопровождается испусканием кванта света
( n > m ):
|
|
mee 4 æ |
1 |
|
|
1 |
ö |
|||||
hn = En - Em |
= |
|
|
|
×ç |
|
|
- |
|
|
|
÷ . |
8h |
2 |
2 |
|
2 |
n |
2 |
||||||
|
|
|
e0 |
è m |
|
|
|
ø |
||||
Отсюда частота излучённого кванта |
|
|
|
|
|
|
|
|
|
|
|
|
n = R |
æ |
1 |
|
|
- |
1 ö |
(4.5) |
||||
ç |
|
|
|
|
|
|
÷ |
||||
|
2 |
|
n |
2 |
|||||||
|
|
èm |
|
|
|
|
ø |
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
R = |
mee 4 |
|
|
|
|
|
|
(4.6) |
|||
8h 3e02 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
- теоретическое формула постоянной Ридберга.
Формула (4.5) - это теоретическая формула Бальмера (сравни с формулой (1.7)). Теоретическое значение постоянной Ридберга, рассчитанное по формуле (4.6), хорошо согласуется с экспериментальным.
Теория Бора сыграла огромную роль в создании атомной физики, в развитии атомной и молекулярной спектроскопии, но её внутренняя противоречивость — соединение классических и квантовых представлений — не позволили на её основе объяснить спектры многоэлектронных атомов (даже простейшего из них — атома гелия, содержащего помимо ядра два электрона).
11 |
12 |
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ I
1. ЛАБОРАТОРНАЯ РАБОТА № 3.49 ОПЫТ ФРАНКА И ГЕРЦА
Цель работы: Убедиться в существовании дискретных энергетических уровней атома. Определить потенциал возбуждения атомов газа. Приборы и принадлежности: Модульный учебный комплекс МУКОК.
Методика измерений.
В данной работе опыт Франка и Герца осуществляется с трубкой заполненной инертным газом, в качестве которой используется газонаполненный триод (тиратрон ТГ1Б.)
Физические явления, протекающие в этой радиолампе, принципиально не отличаются от описанных выше.
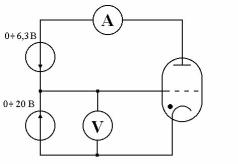
Схема установки представлена на рис.3.
Рис.3
Важно отметить, что напряжение, измеряемое вольтметром, не равно истинному напряжению между катодом и сеткой. Это объясняется тем, что катод и сетка обычно изготавливают из разных металлов. Газ свободных электронов в этих металлах имеет не одинаковое численное значение химических потенциалов. Если такие металлы привести в соприкосновение, то начнется процесс установления термодинамического равновесия между ними, при котором электроны из металла с более высоким значением химического потенциала начнут переходить в металл с относительно низким его значением. Этот переход продолжается до тех пор, пока химические потенциалы ни выровняются. Первый металл, лишаясь некоторого количества своих электронов, заряжается положи-
тельно, в то же время второй, приобретая избыточные электроны, заряжается отрицательно. Состоянию динамического равновесия соответствует определённая установившаяся разность потенциалов между контактирующими металлами, которая называется внешней контактной разностью потенциалов
U КОНТ . Сказанное означает, что истинное напряжение между катодом и сеткой U равно алгебраической сумме напряжения источника UV , которую измеряет вольтметр, и контактной разности потенциалов U КОНТ :
U =UV +U КОНТ . |
(1) |
Для температур, при которых работает тиратрон |
можно считать |
UКОНТ=1,5÷1,7 В. |
|
Задание к работе |
|
1.Соберите схему согласно рис.3. Накал тиратрона уже подключен к источнику питания лампы. Время прогрева установки ~ 3 мин.
2.Установите напряжение на сетке в диапазоне 1÷3В. Установите задерживающее напряжение между сеткой и анодом от 0 до 0,5 В.
3.Снимите зависимость тока анода от напряжения между катодом и сеткой. Данные занесите в таблицу 2. Постройте график этой зависимости.
Таблица 2
I |
0 |
0,25 |
0,5 |
1 |
….. |
2 |
…. |
3 |
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Определите с помощью построенного графика по первому максимуму с учетом контактной разности потенциалов (формула 1) потенциал возбуждения
U ВОЗБ .
5.Зная потенциал возбуждения, используя таблицу 1 (стр.10), определите, каким газом заполнен тиратрон.
6.Рассчитайте длину волны, которую излучают атомы газа, находящиеся в тиратроне.
Контрольные вопросы
1.Что доказал опыт Франка и Герца?
2. Почему столкновения атомов газа с электронами при малых значениях ускоряющего напряжения, приложенного между катодом и сеткой, носят упругий характер?
13 |
14 |
3.Почему столкновения атомов газа с электронами, начиная с определённого значения ускоряющего напряжения, начинают носить неупругий характер?
4.Почему зависимость силы тока коллектора (анода) от напряжения, приложенного между катодом и сеткой, имеет участки плавного роста и резкого спада?
5.Как, зная потенциал возбуждения атома, определить энергию, которая необходима для перевода атома из основного в первое возбужденное энергетическое состояние?
6.Как определить длину электромагнитной волны, которую излучает атом газа при переходе из первого возбуждённого в основное энергетическое состояние?
7.Докажите, что именно при неупругом ударе электрон может передать атому газа наибольшую часть своей кинетической энергии. Какая часть кинетической энергии при этом останется у электрона? (Для простоты рассмотрите столкновение ускоренного полем электрона с неподвижным атомом).
8.Почему не учитываются столкновения нейтральных атомов газа с имеющимися в тиратроне ионами, которые ускоряются тем же полем до тех же кинетических энергий, что и электроны?
2. ЛАБОРАТОРНАЯ РАБОТА № 3.17. СПЕКТРАЛЬНЫЙ АНАЛИЗ
Цель работы: Ознакомление с основными принципами спектрального анализа; изучение оптической схемы спектральных приборов и их характеристик; определение неизвестного элемента по его спектру.
Приборы и принадлежности: Монохроматор УМ-2, ртутная лампа, неоновая лампа, разрядная лампа с неизвестным газом.
Развитие спектрального анализа
Спектральным анализом называется физический метод определения химического состава вещества, основанный на изучении спектра излучения или поглощения электромагнитных волн этим веществом. Различают качественный и количественный анализ. Задачей качественного спектрального анализа является установление всех химических элементов, из которых состоит исследуемый образец. Она решается путем измерения длин волн спектральных линий излучения вещества и отождествления их по таблицам с определенными химическими элементами.
В задачу количественного спектрального анализа входит определение концентраций химических элементов, содержащихся в веществе-источнике излучения. Этот анализ производится путем измерения интенсивностей спектральных линий данного элемента и последующего сравнения их с интенсивностями тех же линий в образцах с известной концентрацией того же элемента.
Спектральный анализ в подавляющем большинстве случаев точнее, быстрее и чувствительнее химических методов и поэтому широко применяется в современном производстве и в научных исследованиях. Особую роль играет спектральный анализ в астрофизике: здесь это единственный экспериментальный метод определения химического состава в строении звезд.
Путь к современным методам, технике и пониманию физических основ спектрального анализа был длинным и непростым. Началом систематического изучения спектров излучения вещества следует считать работы И. Ньютона по преломлению света в призмах. Он первым сформулировал идею о том, что белый свет является составным, т.е. представляет собой смесь лучей различного цвета и различной преломляемости.
В1834 г. Ф. Тальбо первым пришел к заключению: “Когда в спектре пламени появляются какие-либо определенные линии, они характеризуют металл, содержащийся в пламени”. В 1835 г. Ч. Уитстон, исследуя спектр электрической искры, подтверждает эту мысль: линии спектра зависят только от качества электродов, причем для каждого материала характерен свой спектр.
В1854-1859 г.г. физик Г.Р. Кирхгоф и химик Р.Б. Бунзен провели большую серию экспериментов со спектрами излучения различных веществ, возбуждаемых в пламени газовой горелки, и пришли к фундаментальному выводу: “Разнообразие соединений, в которые входили металлы, разнообразие химических процессов, происходивших в различных пламенях, и огромный интервал температур – все это не оказывает никакого влияния на положение спектральных линий отдельных металлов”. Тем самым были сформулированы основы спектрального анализа: однозначная связь вида спектра с химической индивидуальностью атомов данного элемента. Сейчас говорят так: спектры – это паспорта атомов.
Плодотворность спектральных методов не замедлила проявиться: стоило в спектре какого-то соединения обнаружить неизвестные ранее линии, как химическим путем из этого соединения извлекался новый элемент. Так были открыты: рубидий (1860 г.), цезий (1861 г.), таллий (1862 г.), индий (1863 г.), галлий (1875 г.), гелий (1895 г.).
Однако, несмотря на значительные успехи в практическом применении спектрального анализа, вплоть до начала XX века оставались неясными фундаментальные физические вопросы: как устроен атом; почему спектры излучения атомов состоит из отдельных узких линий, тогда как спектры излучения молекул представляет собой набор относительно широких полос; почему спектры всех элементов разные? Иными словами: каков механизм излучения и поглощения света веществом. Ответить на эти вопросы классическая физика не смогла.
Спектральные приборы
Общие характеристики. Спектральные приборы предназначены для анализа сложного излучения, непосредственно излучаемого различными телами или
15 |
16 |
преобразованного в результате взаимодействия излучения с веществом. Эти исследования проводятся в широком диапазоне длин волн от далекой ультрафиолетовой области до миллиметровых радиоволн.
Спектральные приборы позволяют:
а) разложить исследуемое излучение в спектр, т.е. расположить по длинам волн излучение, которое попадает на вход прибора;
б) зафиксировать положение отдельных участков спектра или отдельных спектральных линий;
в) измерить интенсивность какого-либо участка спектра или спектральной линии.
По положению линий в спектре, т.е. по длинам волн, можно судить об уровнях энергии и внутреннем строении атомов и молекул, а по интенсивности линий – о вероятностях переходов между отдельными уровнями. Интенсивность спектральных линий определяется также числом излучающих атомов и молекул, что дает возможность определить содержание отдельных элементов и молекулярных соединений в исследуемом веществе. По форме контура спектральных линий можно сделать заключение о характере взаимодействия между частицами, о влиянии электрических и магнитных полей, а также о температуре, при которой происходит излучение. Таким образом, спектральные приборы исследуют излучение как сигнал, посылаемый в определенных условиях веществом и дающий информацию о его строении.
Различают атомный и молекулярный спектральный анализ. В обоих случаях анализ может проводиться по спектрам излучения и тогда он называется эмиссионным. Анализ по спектрам поглощения именуется абсорбционным.
Спектры излучения атомов обычно получаются при высокой температуре источника света, при которой происходит испарение вещества, расщепление его молекул на отдельные атомы и возбуждение атомов.
При исследовании спектров важно, чтобы в процессе анализа молекулы не изменили своей структуры. Спектры молекул можно изучать и в излучении, и в поглощении. Спектры сложных молекул легче изучать в поглощении, так как при этом они не распадаются.
При абсорбционном анализе свет от источника со сплошным спектром пропускают через исследуемое вещество. При этом часть световой энергии будет избирательно поглощаться атомами или молекулами вещества. В результате на фоне сплошного спектра появятся темные линии и полосы поглощения. По положению, структуре и коэффициенту поглощения этих линий можно узнать состав и строение исследуемого вещества.
Принципиальная схема спектрального прибора и назначение отдельных узлов.
Спектральный прибор состоит из трех основных частей: осветительной, диспергирующей и приемно-регистрирующей.
Осветительная часть включает источник излучения и фокусирующую оптику, при помощи которой освещается узкая входная щель прибора.
Спектральная часть состоит из входной щели, диспергирующей и фокусирующей систем (рис.2).
Входная щель (3 на рис.2) является вторичным источником немонохроматического света или “предметом” по отношению ко всей последующей оптической части прибора. Изображение щели, разложенное диспергирующей системой по длинам волн и сфокусированное на выходе прибора и представляет собой наблюдаемый спектр источника излучения.
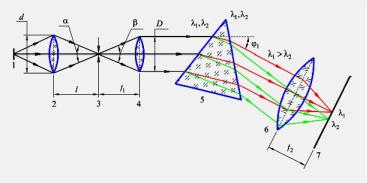
Рис. 2. Оптическая схема призменного спектрального прибора:
1 - источник света – исследуемое вещество; 2 - конденсорная линза; 3 - узкая входная щель; 4 - коллимирующий объектив; 5 - призма – диспергирующий элемент; 6 - фокусирующий объектив; 7 - фокальная плоскость – плоскость формирования спектра излучения.
В принципе спектральный прибор можно построить и без входной щели, используя в качестве предмета непосредственно источник излучения. Но все реальные источники имеют значительные размеры и после разложения в спектр их монохроматические изображения частично наложатся друг на друга и их невозможно будет различить. Чтобы избежать этого, на пути лучей ставится узкая щель и ее монохроматические изображения получаются в виде резких линий. Именно форме изображения щели в свете той или иной длины волны обязано появление термина “спектральная линия”.
Однако уменьшать ширину щели разумно лишь до определенного предела, обусловленного дифракцией, ниже которого дальнейшее ее сужение уже приводит не к уменьшению ширины спектральных линий, а, наоборот, к увеличению. Этот предел называется нормальной шириной щели и равен
Smin = |
f1l |
(2) |
|
D |
|||
|
|
17 |
18 |
где D - диаметр пучка света, падающего на призму, а затем на фокусирующий объектив
При любой ширине щели S ³ Smin дифракционными явлениями на ней
можно пренебречь и рассматривать ход лучей в приборе по законам геометрической оптики.
Часть прибора, включающая щель 3 и первый по ходу лучей объектив 4 на рис.2, называется коллиматором. Его назначение – создать параллельные пучки лучей. Поэтому щель всегда ставится в фокусе объектива, а сам объектив должен быть ахроматическим, т.е. его фокусное расстояние не должно зависеть от длины волны.
Для получения максимальной интенсивности спектра объектив коллиматора должен быть полностью заполнен светом. Это достигается специальным выбором условий освещения щели.
Источник света с большой равномерной излучающей поверхностью можно расположить непосредственно перед щелью. Если угловая ширина источника (рис.2), не меньше углового размера коллимирующего объектива, то коллиматор заполнен светом. При этом никакая осветительная система не может увеличить световой поток, приходящий в прибор. Из условия a = b (рис.2) сле-
дует, что источник диаметром d должен располагаться от щели (2) на расстоянии
l = |
f1d |
(3) |
|
D |
|||
|
|
Если источник света мал или по техническим причинам его нельзя расположить близко к щели, чтобы выполнялось условие (3), пользуются линзовыми осветительными системами, формирующими изображение источника на входной щели спектрального прибора, как показано на рис. 2. В этом случае в условии (3) d – диаметр апертуры конденсорной линзы, l – расстояние от линзы до входной щели.
Диспергирующая система предназначена для пространственного разделения пучков света различных длин волн. В качестве диспергирующих элементов используются призмы, дифракционные решетки, а также интерферометр Фаб- ри-Перо и другие приборы. Рассмотрим ход лучей в призменном спектральном
приборе (рис.2). Пусть источник 1 излучает свет только двух длин волн l1 и
l2 .
Лучи другой длины волны также выйдут из призмы параллельным пучком, но в другом направлении, под углом j2 , т.к. n1 (l) ¹ n2 (l) (рис. 2 и 3).
Так призма осуществляет пространственное разделение световых пучков различных длин волн. Объектив камеры 6 собирает параллельные пучки света, выходящие из призмы, в своей фокальной плоскости 7 (Рис. 2)
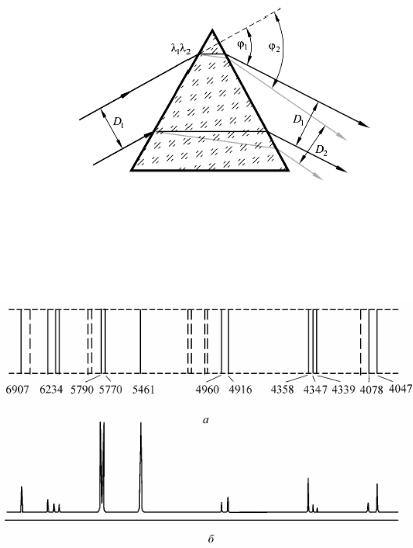
Рис. 3. Ход лучей света двух разных длин волн l1 и l2 через призму.
Так как лучи различных длин волн имеют после призмы различные направления, то в фокальной плоскости объектива камеры получается ряд параллельных, различно окрашенных изображений щели, образующих систему спектральных линий – спектр излучения источника (рис. 4, а).
Рис. 4. Система спектральных линий излучения ртути (а) и соответствующее распределение интенсивности света в спектре (б)
19 |
20 |
