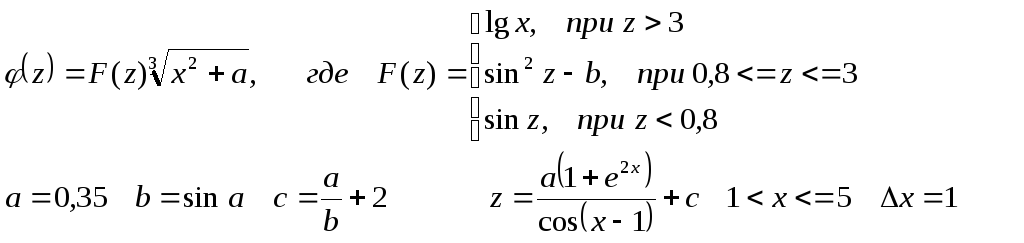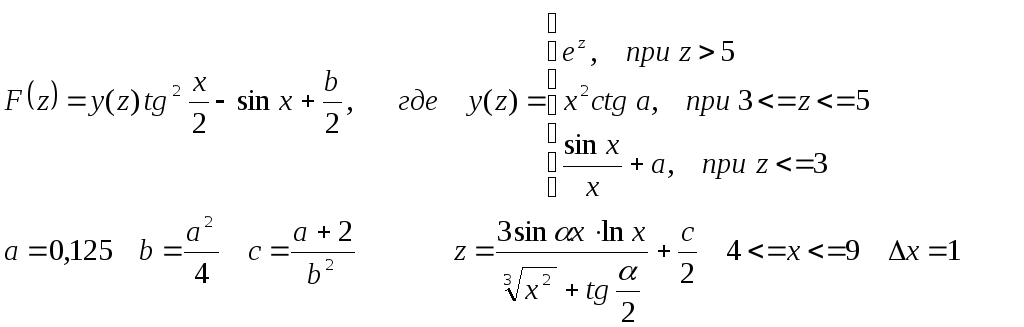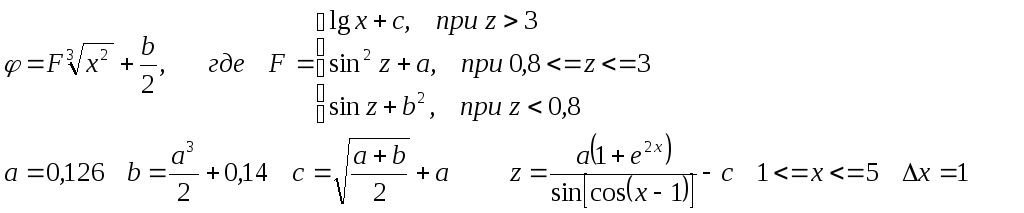Табулирование функций
Задача 1
Протабулировать функции y, z и q на данном диапазоне аргумента x. Построить графики этих функций в одной системе координат.
Диапазон изменения аргумента 1 x 4 с шагом 0,1;
,
,
1. Построить таблицу значений функций для соответствующего аргумента.
1
.1.
Заполнить столбецx
автозаполнением с помощью прогрессии.
В ячейку А2 набрать данное начальное
значение x
и нажать кнопку ввода на cтроке
формул. Выбрать команду Главная
/ Редактирование
/ Прогрессия.
В появившемся диалоговом окне отметить
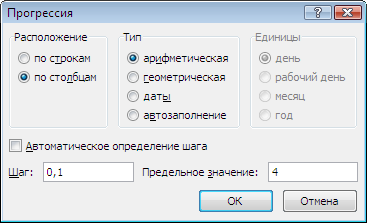
1.2. В ячейку В2 ввести формулу:
=(1/tan(A2/2)+(A2^2+4)^(1/3)) / (exp(abs(A2))+4)+cos(A2/3)^2
1.3. В ячейку С2 ввести формулу:
=B2^2 + A2^3/2
1.4. В ячейку D2 ввести формулу: =С2^2 + B2^2
В итоге получим значения функций y, z и q для x = 1. Для того, чтобы распространить формулы на соседние ячейки и найти значения функций для остальных значений аргумента x нужно использовать маркер заполнения (черный квадратик в нижнем правом углу активной ячейки). Установить на него курсор и протянуть мышкой маркер заполнения до предельного значения аргумента.
При копировании формул маркером вертикально вниз в относительных адресах будут автоматически меняться номера строк. Формулы пересчитываются для соответствующего значения аргумента.
2. Построение графиков функций.
В Excel имеется возможность графического представления данных в виде диаграмм. Диаграммы связаны с данными листа, на основе которых они были созданы, и изменяются каждый раз, когда изменяются данные на листе.
Порядок работы с мастером диаграмм.
1. Выделить полученную таблицу.
2. Выбрать команду Вставка. На ленте выбрать Диаграммы / Точечная (последний вид).
3. Настроить шкалу x. В появившемся графике с помощью правой клавиши мыши вызвать контекстное меню шкалы x. Выбрать команду Формат оси. В диалоговом окне в пункте Параметры оси выбрать фиксированные значения и ввести данные в соответствующие строки.
Изменить ширину линии и цвет можно в этом же окне, выбрав пункты Тип линии и Цвет линии соответственно.
4. Линии сетки. При выделенном графике использовать команду Макет / Сетка. Горизонтальные и вертикальные линии выбрать основные и промежуточные.
Результат показан на рисунке 1.
Рис. 1. Табулирование функций
Задача 2
Протабулировать функции y, g и z на данном диапазоне аргумента x. Построить графики этих функций в одной системе координат.
,
,
При значениях аргумента -2 х 2 с шагом 0,1.
1. Построить таблицу значений функций для соответствующего аргумента.
Выполнить п. 1.1. задачи 1.
1.2. В ячейку В2 ввести формулу:
=(1+cos(A2)) / (1+exp(2*A2))
1.3. В ячейку С2 ввести формулу:
=Если (А2<=0; (3+sin(2*A2)^2) / (1+cos(A2)^2); 2*(1+2*A2)^(1/2))
1.4. В ячейку D2 ввести формулу:
=Если (A2<0; (1+A2^2 / (1+A2^2))^(1/2); Если(A2>1; (1+(ABS(2*sin(3*A2)))^(1/3))^(1/2); 2*cos(A2)^2)).
Заполнить остальные ячейки столбца с помощью маркера заполнения.
Формулы п. 1.3. и п. 1.4. этой задачи можно вводить с помощью мастера функций.
Выбрать команду Формулы / Вставить функцию / категория логические Если. В появившемся окне заполнить строки следующим образом:
Рис. 2. Вычисление функция g
Рис. 3а. Вычисление функции z
Установить курсор в третью строку Значение_если_ложь, выбрать мышью в строке формул функцию Если. В появившемся новом окне заполнить строки следующим образом:
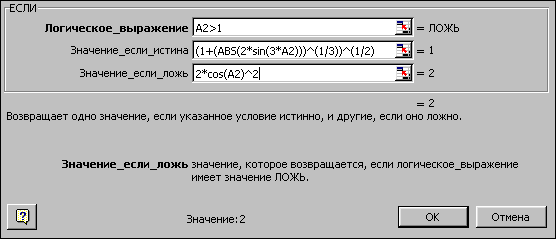
Рис. 3б. Вычисление функции z
2. Построить график функций см. п.2 задачи 1.
Результат показан на рисунке 4.
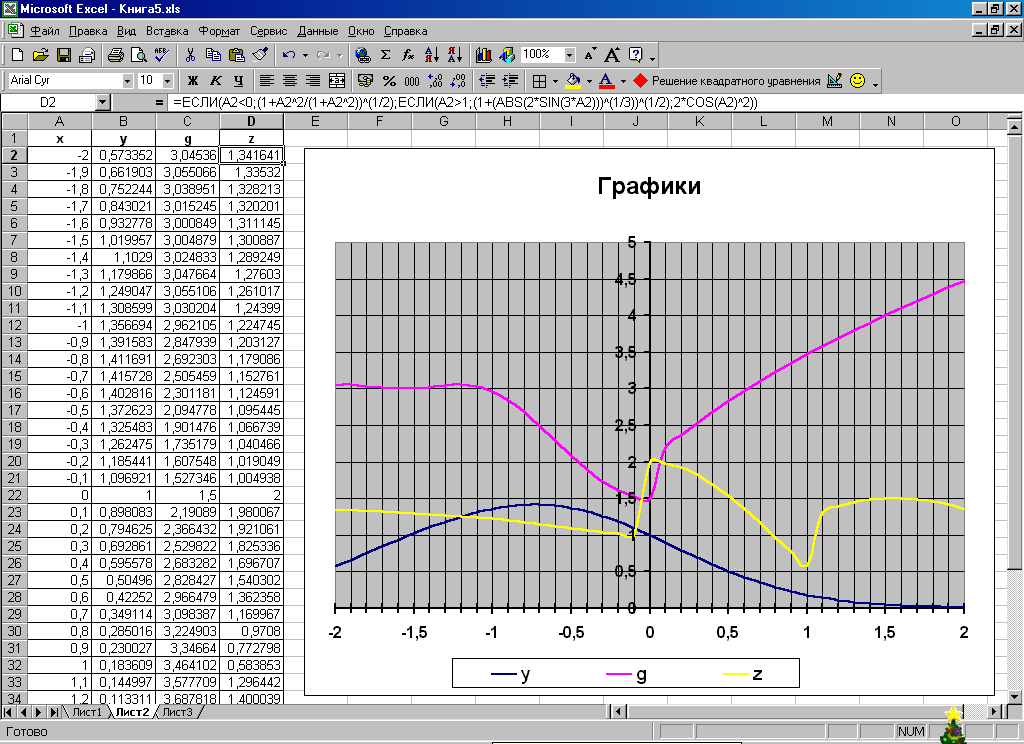
Рис. 4.
Задача 3
Протабулировать функции k и z на данном диапазоне аргумента x. Построить графики этих функций в одной системе координат.
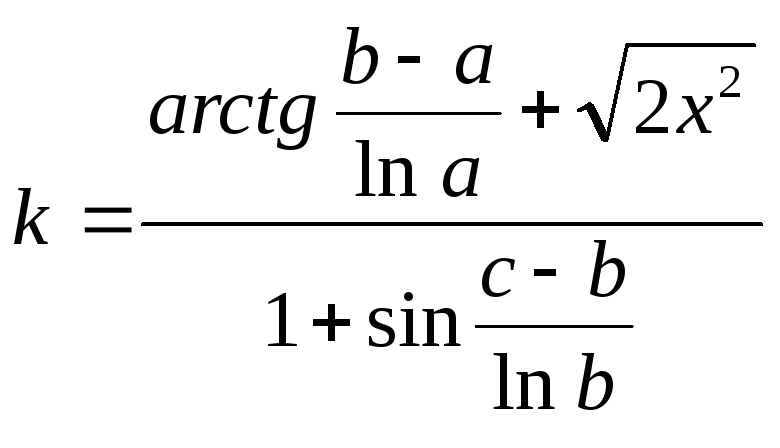
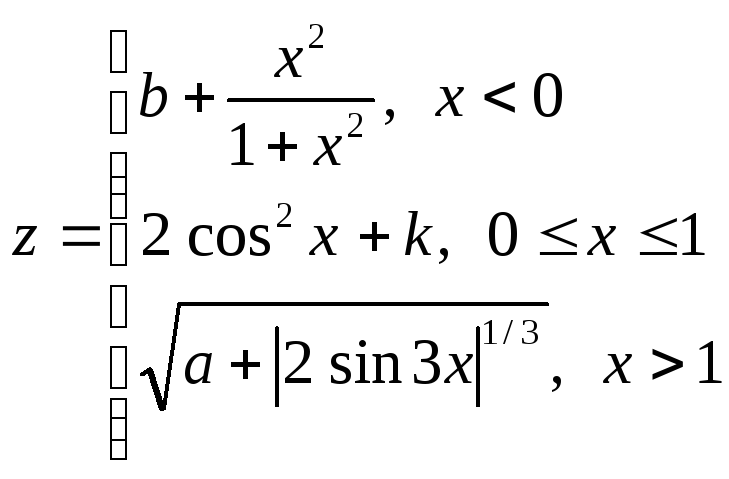
При значениях аргумента -2 х 2 с шагом 0,1.
Константы
a =2,2 b = 1,8 c = a + b
1. Построить таблицу значений функций для соответствующего аргумента.
Выполнить п. 1.1. задачи 1.
1.2. В ячейку В2 ввести формулу:
=( atan(($F$2 – $E$2) / ln($E$2)) + (2*A2)^(1/2) ) / ( 1 + sin(($G$2 – $F$2) / ln($F$2)) )
1.3. В ячейку С2 ввести формулу:
=Если (A2<0; $F$2 + A2^2 / (1 + A2^2); Если (A2>1; ( $E$2 + (abs(2*sin(3*A2)))^(1/3) )^(1/2); 2*cos(A2)^2 + B2))
Заполнить остальные ячейки столбца с помощью маркера заполнения.
2. Построить график функций см. п.2 задачи 1.
Результат показан на рисунке 5.
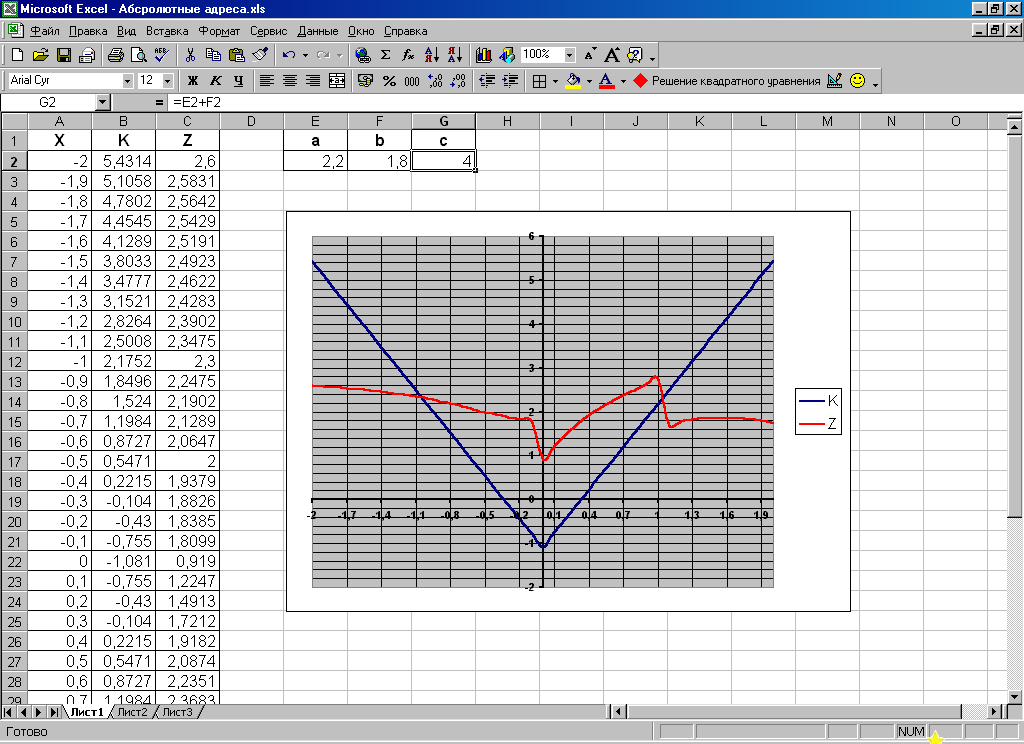
Рис. 5.
Варианты заданий к задаче 1
Вариант 1
,
Диапазон изменения аргумента -3 ≤ x ≤ 3 с шагом Δx = 0,3
Вариант 2
,
Диапазон изменения аргумента -2 ≤ x ≤ 2 с шагом Δx = 0,2
Вариант 3
,
,
Диапазон изменения аргумента 2 ≤ x ≤ 3 с шагом Δx = 0,1
Вариант 4
,
Диапазон изменения аргумента -0,3 ≤ x ≤ 3 с шагом Δx = 0,25
Вариант 5
,
,
Диапазон изменения аргумента 2 ≤ x ≤ 3 с шагом Δx = 0,08
Вариант 6
,
,
Диапазон изменения аргумента 3 ≤ x ≤ 4 с шагом Δx = 0,05
Вариант 7
,
,
Диапазон изменения аргумента -2 ≤ x ≤ 4 с шагом Δx = 0,7
Вариант 8
,
Диапазон изменения аргумента -1 ≤ x ≤ 3 с шагом Δx = 0,1
Вариант 9
,
Диапазон изменения аргумента 2 ≤ x ≤ 9 с шагом Δx = 0,8
Вариант 10
,
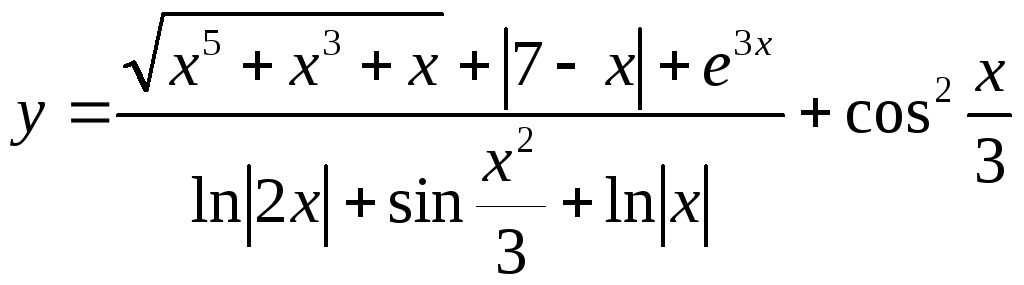Диапазон изменения аргумента 2 ≤ x ≤ 4 с шагом Δx = 0,3
Вариант 11
,
Диапазон изменения аргумента -2 ≤ x ≤ 5 с шагом Δx = 0,3
Вариант 12
,
Диапазон изменения аргумента -7 ≤ x ≤ 2 с шагом Δx = 0,7
Вариант 13
,
Диапазон изменения аргумента -5 ≤ x ≤ 6 с шагом Δx = 0,8
Вариант 14
,
Диапазон изменения аргумента -4 ≤ x ≤ 3 с шагом Δx = 0,7
Вариант 15
,
Диапазон изменения аргумента -4 ≤ x ≤ 4 с шагом Δx = 0,6
Вариант 16
,
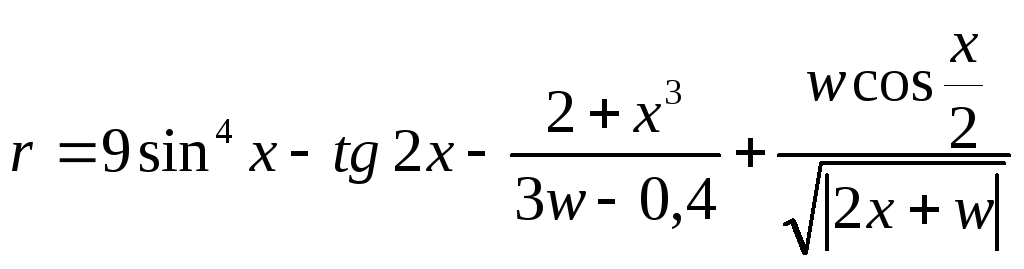
Диапазон изменения аргумента -2 ≤ x ≤ 4 с шагом Δx = 0,5
Вариант 17
,
Диапазон изменения аргумента -2 ≤ x ≤ 2 с шагом Δx = 0,4
Вариант 18
,
Диапазон изменения аргумента -2 ≤ x ≤ 2 с шагом Δx = 0,5
Вариант 19
Диапазон изменения аргумента -1 ≤ x ≤ 2 с шагом Δx = 0,3
Вариант 20
Диапазон изменения аргумента -1 ≤ x ≤ 1 с шагом Δx = 0,2
Варианты заданий к задаче 2
Диапазон изменения аргумента для всех вариантов -2 ≤ x ≤ 2 с шагом Δx = 0,1
Вариант 1
,
,
Вариант 2
,
,
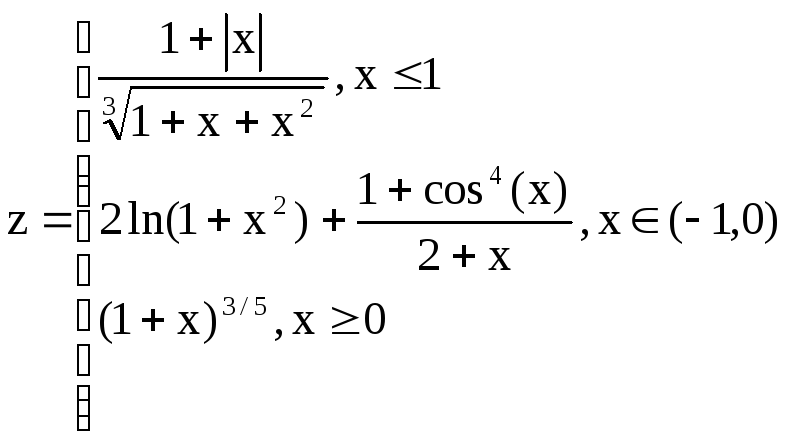
Вариант 3
,
,
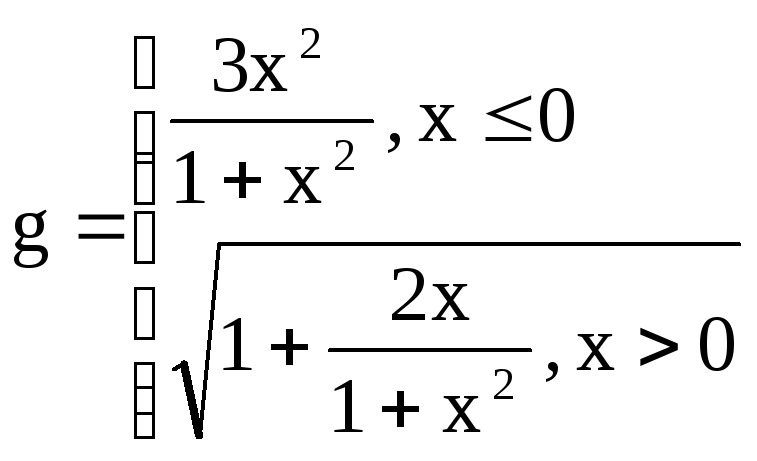Вариант 4
,
,
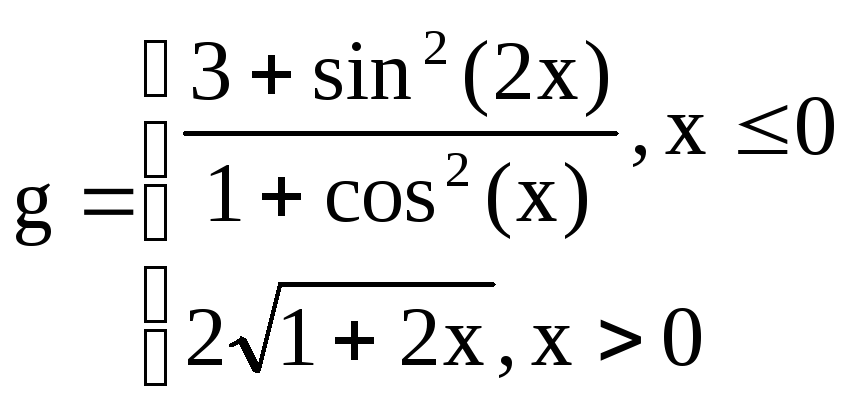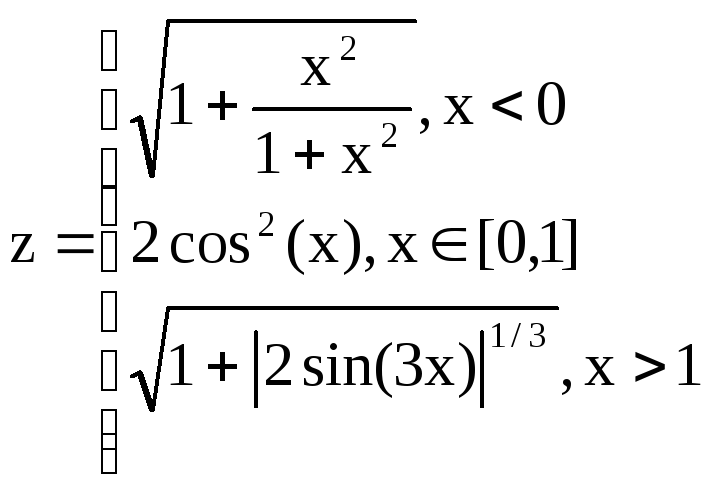
Вариант 5
,
,
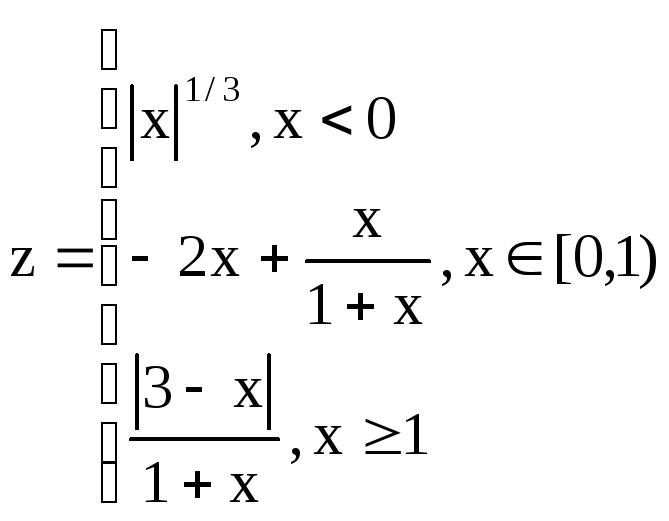
Вариант 6
,
,
Вариант 7
,
,
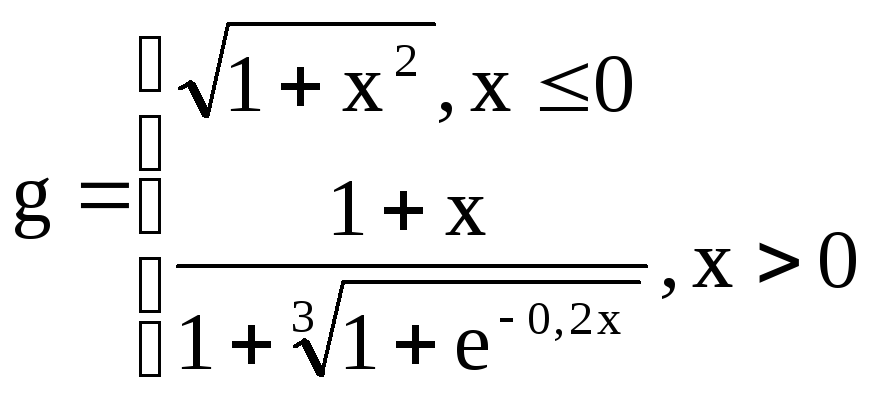Вариант 8
,
,
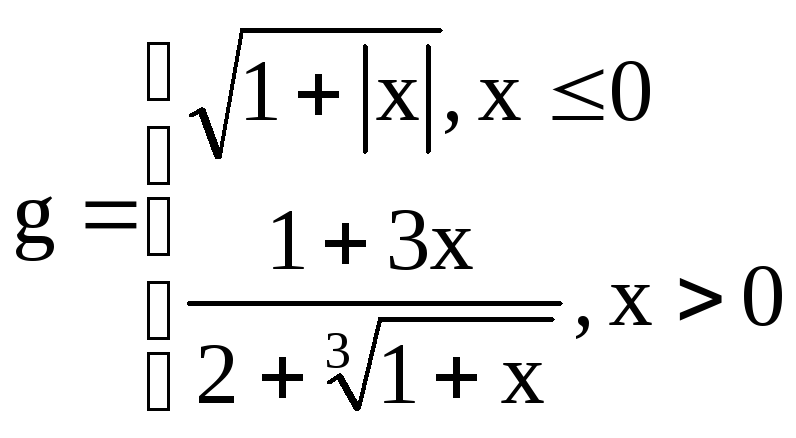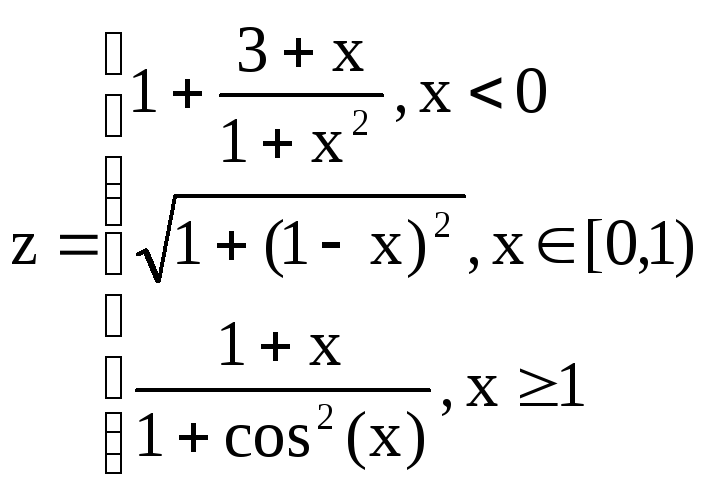
Вариант 9
,
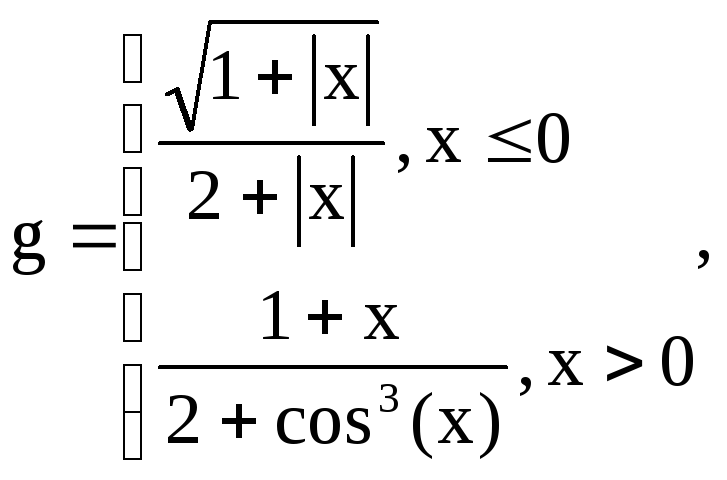
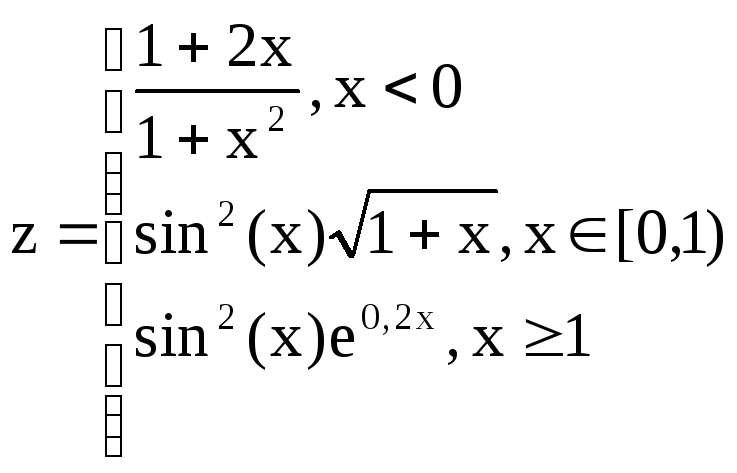
Вариант 10
,
,
Вариант 11
y=cos2(πx),
,
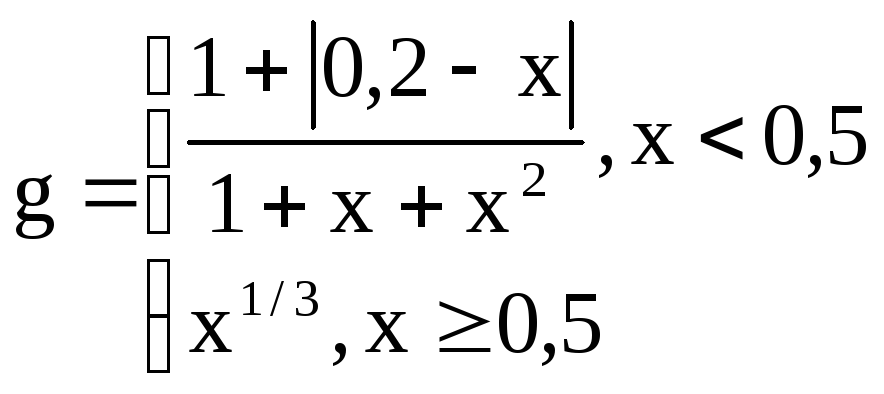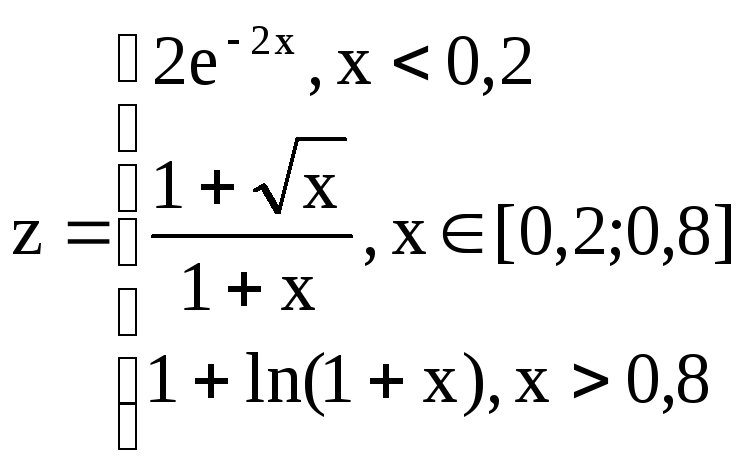
Вариант 12
,
,
Вариант 13
,
,
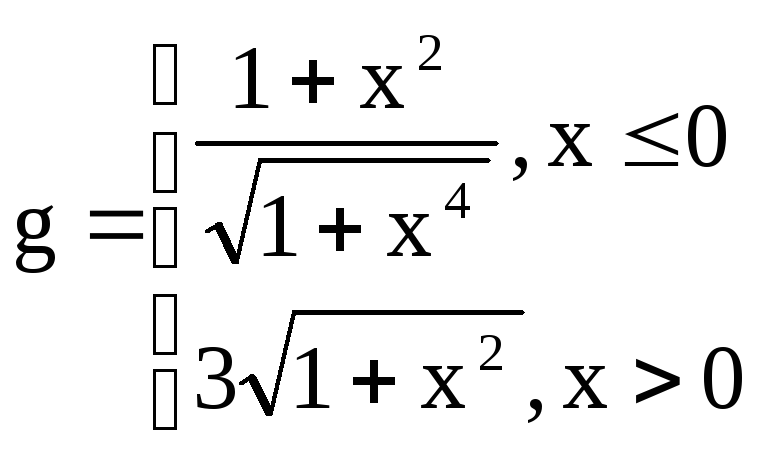Вариант 14
,
,
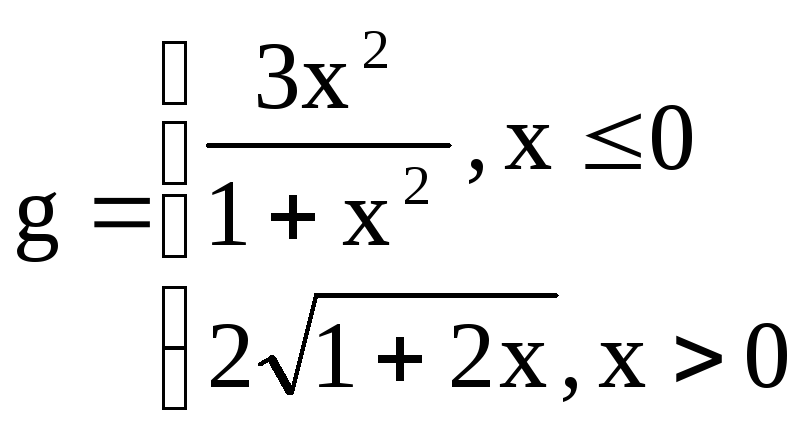Вариант 15
,
,
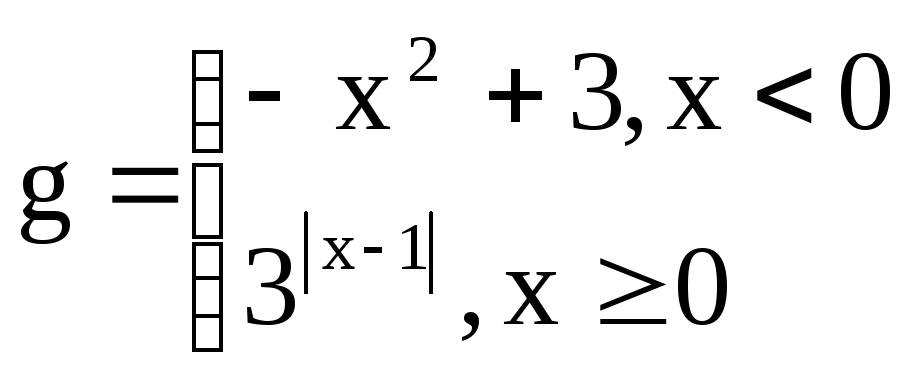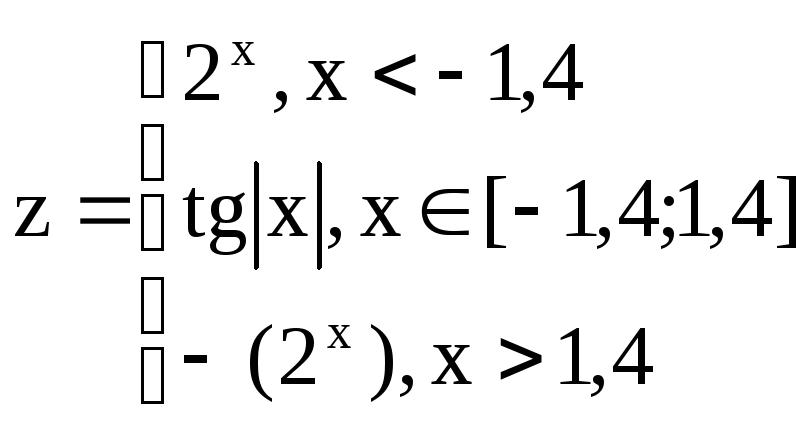
Вариант 16
,
,
Вариант 17
,
,
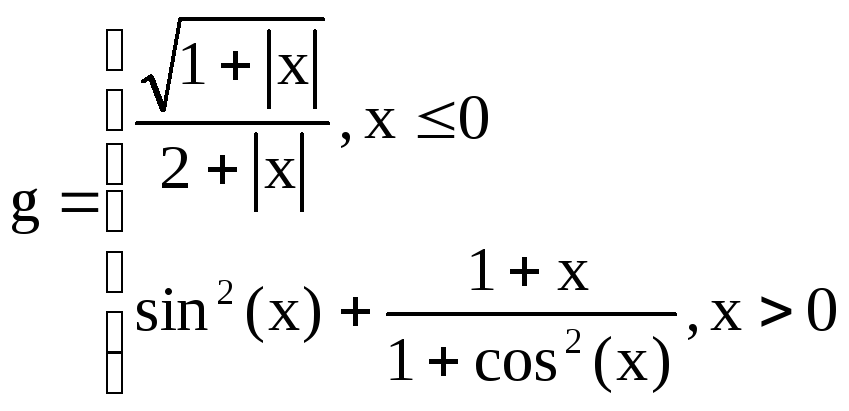Вариант 18
,
,
Вариант 19
,
,
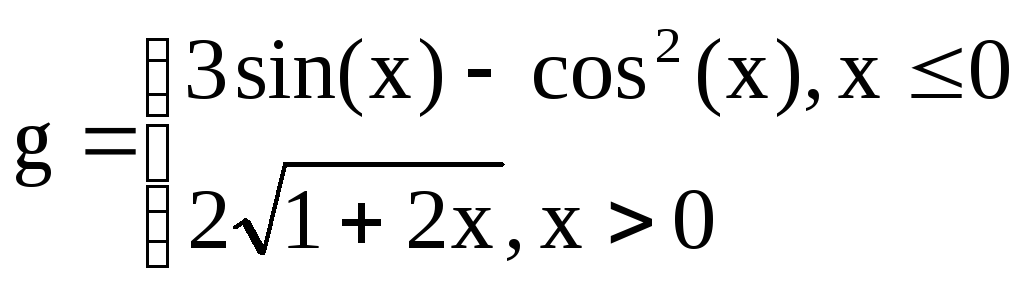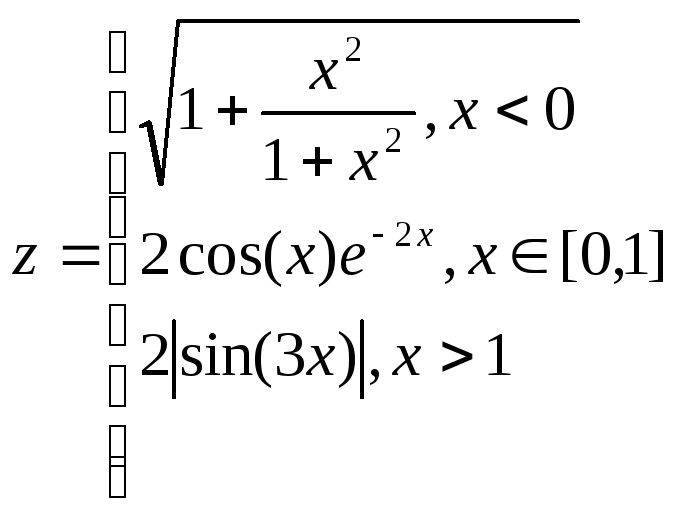
Вариант 20
,
,
Варианты заданий к задаче 3
|
Вариант 1
|
|
Вариант 2
|
|
Вариант 3
|
|
Вариант 4
|
|
Вариант 5
|
|
Вариант 6
|
|
Вариант 7
|
|
Вариант 8
|
|
Вариант 9
|
|
Вариант 10
|
|
Вариант 11
|
|
Вариант 12
|
|
Вариант 13
|
Вариант 14
,
где
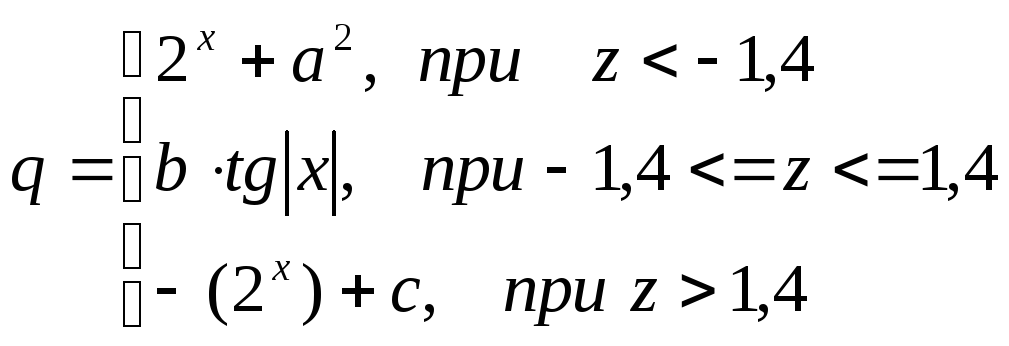
1<=
x<=
3 Δx=0,3
Вариант 15
,
где
1<=
x <= 5 Δx
= 0,8
Вариант 16
,
где
-1<=x<=1
Δx=0,2
Вариант 17
,
где
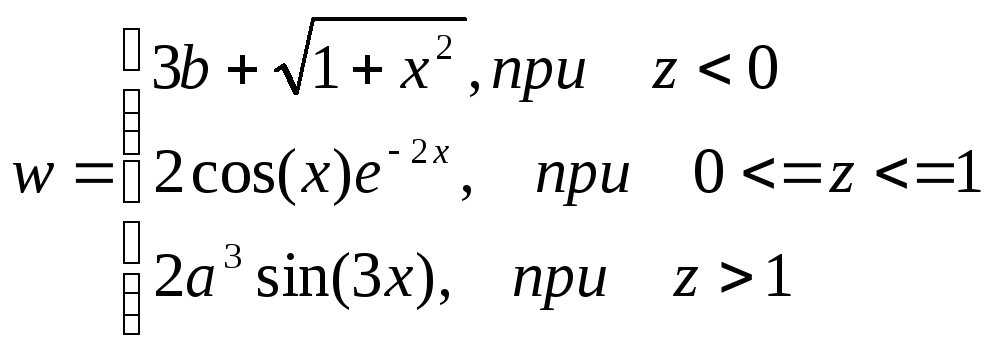
2<=x<=5
Δx=0,4
Вариант 18
,
где
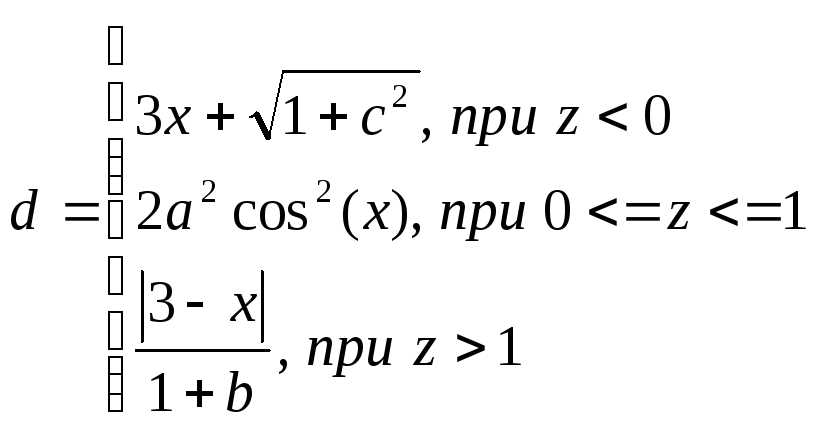
3<=x<=7
Δx=0,5
Вариант 19
,
где
1<=x<=6
Δx=0,2
Вариант 20
,
где
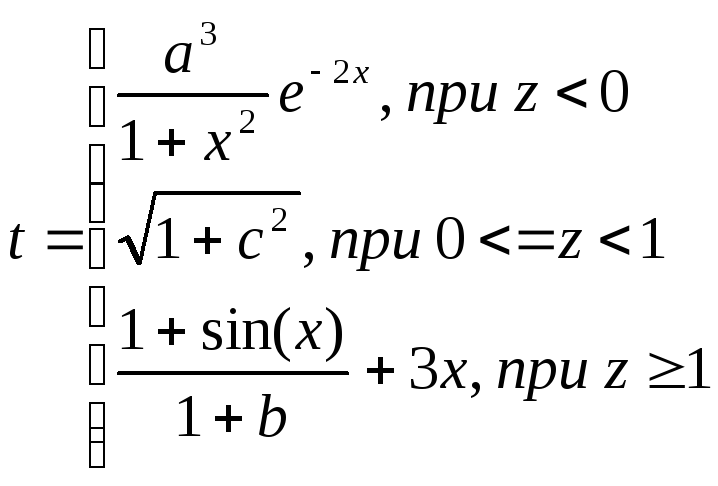
1<=x<=10
Δx=0,5