Порядок выполнения работы

1. Установить стержень горизонтально. Поднять шарик над стержнем на некоторую высоту (указанную преподавателем) и отпустить его.

2. В момент удара шарика о стержень включить секундомер.

3. Наблюдая за одним из концов стержня, определить число оборотов, совершенных стержнем до остановки. В момент остановки стержня выключитьсекундомер.Опыт повторить 5 раз.

4. Рассчитать средние значения скоростейипо средним значениямизмеренных величин.

5. Найти момент инерции стержня I.

6. Используя полученное значение момента инерции, найти момент силтрения в подшипнике оси вращения.

7. Данные измерений и вычислений занести в таблицу

№	m	h	t	n	r			I
1
2
3
среднее

8. Оценить погрешности измерений (по указанию преподавателя).

Контрольные вопросы

1. Что такое момент инерции твёрдого тела? Каков его физический смысл?

2. Что такое момент импульса материальной точки? Чему равен моментимпульса шарика до и после удара?

3. Чему равен момент импульса твёрдого тела? Каково его направление?

4. Сформулируйте закон сохранения момента импульса. Обоснуйте его применение к системе "шарик – стержень".

5. Запишите закон сохранения механической энергии для системы "шарик – стержень".

6. Выведите формулу (8.6) скорости шарика перед ударом.

7. Выведите формулу (8.8) начальной угловой скорости стержня.

8. Выведите формулу (8.5) для расчета момента инерции стержня.

9. Запишите основной закон динамики вращательного движения. Поясните формулу (8.11).

Литература

1. Савельев И. В. Курс физики. Т. 1. – М.: Наука, 1989. – С. 94–116.

2. Трофимова Т. И. Курс физики. – М.: Высш. шк., 2001. – С. 34–46.

Работа 1.9

Изучение прецессионного движения гироскопа

Цель работы: 1) измерить скорость прецессии гироскопа и угловую скорость вращения гироскопа; 2) построить график зависимости угловой скорости прецессии гироскопа от величины внешнего момента силы.

Приборы и принадлежности: гироскоп, закреплённый вкардановом подвесе, угловая шкала, секундомер, масштабная линейка, набор грузов.

Описание установки и метода измерений

Гироскопом называется симметричное твёрдое тело, быстро вращающееся вокруг одной из главных осей инерции. Чтобы ось гироскопа могла свободно поворачиваться в пространстве, его закрепляют на кольцах так называемого карданова подвеса (рис. 9.1), в котором оси внутреннего уу и внешнего zz колец и ось гироскопа хх пересекаются в одной точке, называемой центром подвеса. Такой гироскоп имеет три степени свободы и может совершать любой поворот около центра подвеса.

Г

Рис. 9.1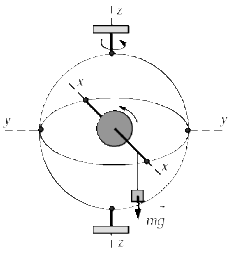

ироскоп характеризуется двумя основными свойствами. Первое свойство гироскопа с тремя степенями свободы состоит в том, что его ось стремится устойчиво сохранять в мировом пространстве приданное ей первоначальное направление. Если эта ось вначале направлена на какую-либо звезду, то при любых перемещениях прибора и случайных толчках она будет продолжать указывать на эту звезду, меняя свою ориентировку относительно осей, связанных с Землёй.

Второе свойство гироскопа обнаруживается, когда на его ось начинает действовать сила, приложенная в точке, не совпадающей с центром масс гироскопа. Казалось бы, что под действием силы ось гироскопаxxдолжна начать поворачиваться вокруг осиyy, а она начинает поворачиваться вокруг осиzz, т. е. вокруг направления действия силы. Это свойство получило названиегироскопического эффекта. Вращение же оси вращения гироскопа вокругнаправления действия силы называется прецессией.

Поведение гироскопа, на первый взгляд, противоестественное, полностью объясняется основным законом динамики вращательного движения (см. формулу на с. 22), который в этом случае удобно записать в виде

. (9.1)

Из (9.1) следует, что внешний момент силы за промежуток временивызывает изменение момента импульса, направленное параллельно вектору момента внешней силы. Наглядно представить поведение гироскопа можно с помощью рис. 9.2.

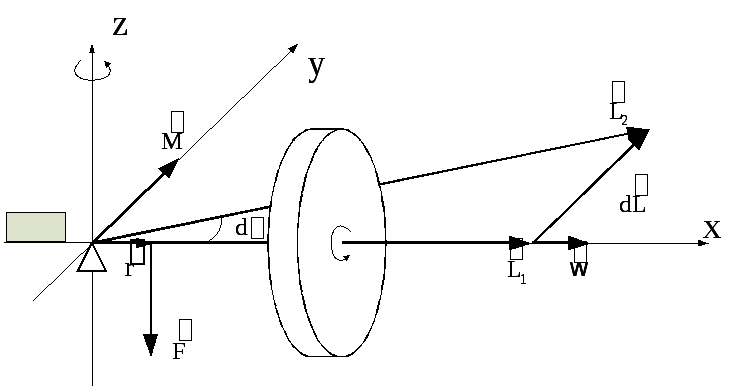
Рис. 9.2

На рис. 9.2 гироскоп вращается вокруг оси x. Следовательно, и его угловая скорость, и момент импульсанаправлены вдоль осиx. При действии на ось гироскопа внешней силы, направленной вдоль осиz, возникает момент силы, который, согласно определению момента силы,направлен вдоль оси y, перпендикулярно плоскости рисунка.Т. е. векторперпендикулярен вектору , а это значит, что он не может изменить модуль момента импульса, а изменяет только направление вектора.

Таким образом, конец вектора , а следовательно, ось вращения гироскопаx, описывает окружность вокруг осиz.Говорят, что ось вращения гироскопа прецессирует вокруг осиz.

Прецессия происходит с постоянной угловой скоростью . Ее легко измерить на опыте, определив угол , на который поворачивается ось гироскопа за время

. (9.2)

Угловая скорость прецессии связана с величиной внешнего момента силы и угловой скоростью вращения гироскопа. Рассмотрим бесконечно малый промежуток времени dt. Угол, на который ось гироскопа повернётся за это время, также бесконечно мал, поэтому длина векторапрактическисовпадает с длиной дуги, которую за это время описывает конец вектора .