Контрольные вопросы

1. Какие системы тел называются замкнутыми, какие – консервативными?

2. Почему система соударяющихся тел может считаться замкнутой?

3. Какая величина называется импульсом тела, импульсом системы тел?

4. Сформулируйте закон сохранения импульса и запишите его для абсолютно упругого и абсолютно неупругого ударов.

5. Запишите закон сохранения энергии для абсолютно упругого и абсолютно неупругого ударов.

6. Запишите законы сохранения импульса и энергии для удара, рассматриваемого в данной работе.

7. Как в данной работе находят скорости шаров до и после удара ?

8. Выразите скорости шаров через углы их отклонения от положения равновесия. Получите формулу (7.12) для проверки закона сохранения импульса.

9. Чему равен коэффициент восстановления энергии? Каков его физический смысл? Получите формулу (7.13) для расчета коэффициента восстановления энергии.

Литература

1. Савельев И. В. Курс физики. Т. 1. – М: Наука, 1989. – С. 94–116.

2. Трофимова Т. И. Курс физики. – М: Высшая шк., 2001. – С. 17–43.

3. Зисман Г. А., Тодес О. М. Курс обшей физики. Т. 1. – М.: Наука, 1972. –

С. 24–46.

Работа 1.8

Определение момента инерции тела и момента сил трения в подшипнике

Цель работы:определить момент инерции вращающегося тела неправильной формы и момент сил трения в подшипнике.

Приборы и принадлежности: вращающееся тело, шарик, секундомер, масштабная линейка.

Описание установки и метода измерений

В

Рис. 8.1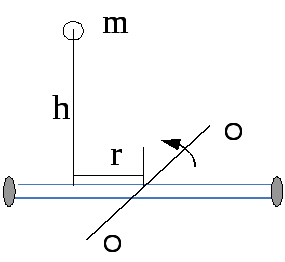

ращающееся тело в виде стержня неправильной формы закреплено на осиОО, проходящей через его центр масс (рис. 8.1). Шарик массойm, свободно падающий с высотыh, ударяется о стержень на расстоянииrот оси вращения. В результате удара стержень начинает вращаться, а шарик либо отскакивает вверх, либо продолжает движение вниз с изменившейся скоростью. Из-за трения в подшипнике спустя некоторое времяtтело останавливается, сделав nоборотов.

При ударе систему "шарик – тело" можно считать замкнутой и поэтому для неё можно записать закон сохранения момента импульса.

Перед ударом тело неподвижно, следовательно, момент импульса системы непосредственно перед ударом равен толькомоменту импульса шарика, который можно считать точкой,

, (8.1)

где – радиус-вектор точки, в которойпроисходитудар, – скорость шарика перед ударом.

После удара момент импульса системы складывается из момента импульса шарика и момента импульса вращающегося тела

, (8.2)

где – скорость шарика после удара,I– момент инерции тела,– начальная скорость вращения, которую тело приобретает в момент удара.

Итак, закон сохранения момента импульса для системы "шарик – тело" имеет вид

.

В последнем выражении все величины направлены по одной прямой, поэтому в скалярной форме оно выглядит так:

. (8.3)

Уравнения (8.3) недостаточно для определения момента инерции тела I. Но если удар считать абсолютно упругим (практически так оно и есть), то для системы "шарик – тело" можно записать закон сохранения механической энергии

, (8.4)

где и–кинетические энергии шарика до и после удара,–кинетическая энергия тела непосредственно после удара.

Исключив из системы уравнений (8.3) и (8.4) скорость шарика после удара (которую практически невозможно найти), получим формулу для расчета момента инерции тела

. (8.5)

Скорости илегко определить на опыте. Если сопротивлением воздуха пренебречь, то для шарика можно записать закон сохранения механической энергии

,

откуда . (8.6)

Начальную угловую скорость тела находят, руководствуясь следующими соображениями. После удара вращение тела является равнозамедленным, следовательно, описывается уравнениями

, (8.7)

где t– время, в течение которого тело останавливается;– угол, на который оно поворачивается за это время,– угловое ускорение вращающегося тела;– угловая скорость тела в момент времениt.

Поскольку = 0, то из (8.7) получается

. (8.8)

Угол можно найти, зная число оборотовn, совершенных телом до остановки. Так как поворот на один оборот соответствует повороту на угол 2радиан, то, и (8.8) принимает вид

. (8.9)

Данные, полученные выше, позволяют, пользуясь основным законом динамики вращательного движения, найти момент силы трения в подшипнике

. (8.10)

Выразив угловое ускорение из (8.7) и подставив его в (8.10), получают окончательную формулу для расчета момента силы трения в подшипнике

. (8.11)