Порядок выполнения работы

1. Закрепить грузы 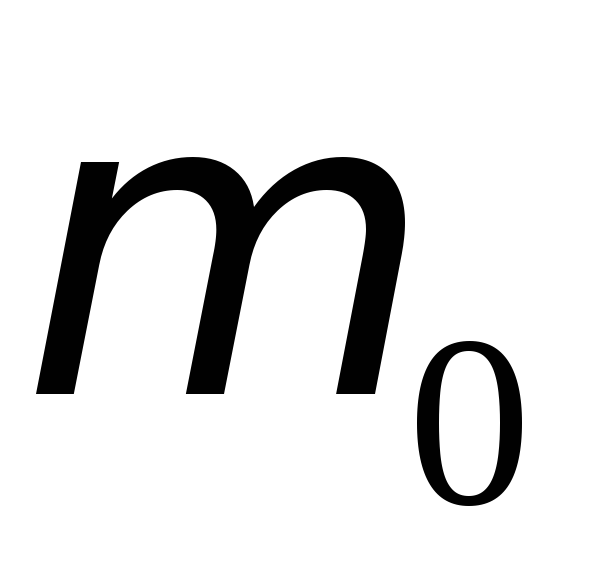на расстоянииот оси вращения маятника (указанном преподавателем), добившись его безразличного равновесия.

2. Определить пять раз время падения груза m.

3. Рассчитать экспериментальное и теоретическое значения момента инерции маятника при данном расположении грузов .

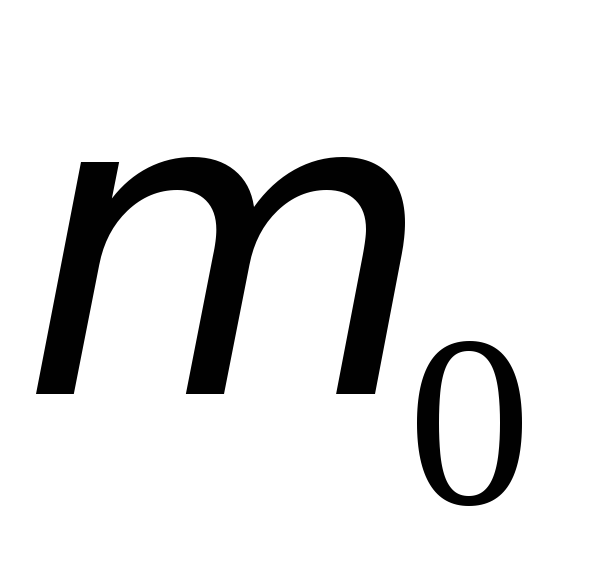4. Результаты измерений и вычислений занести в таблицу

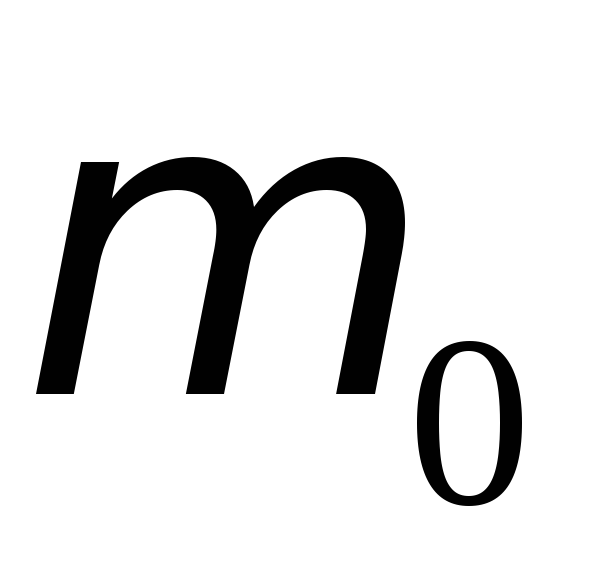
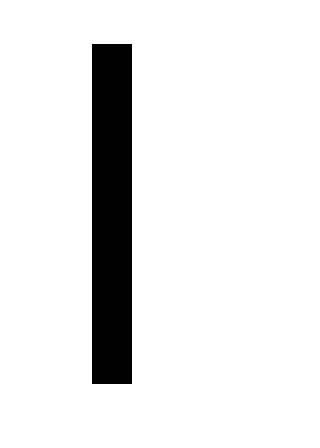
   №		R			t	t	h
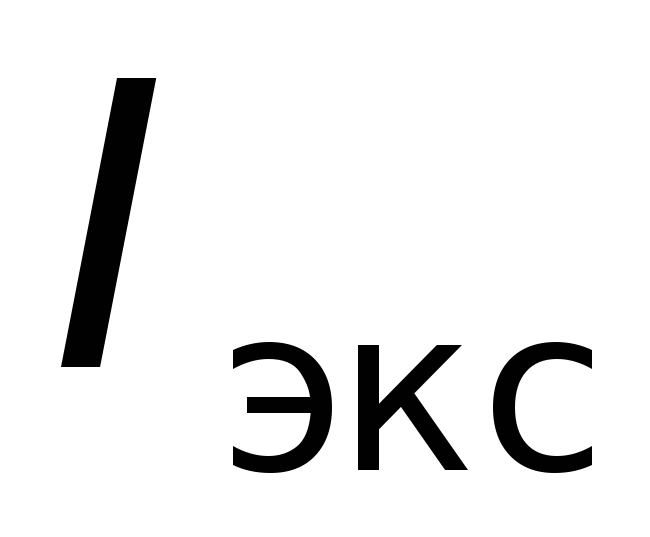
   1
   2
   3
   4
   5

5. Рассчитать (по указанию преподавателя) погрешности 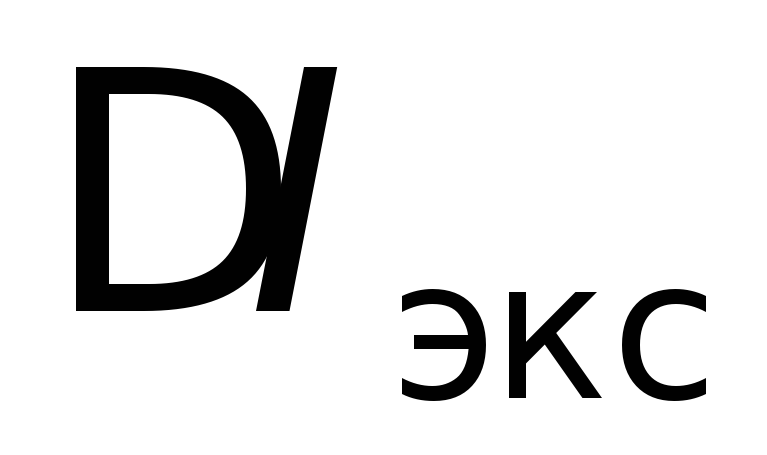и.

6. Убедиться в равенстве значений 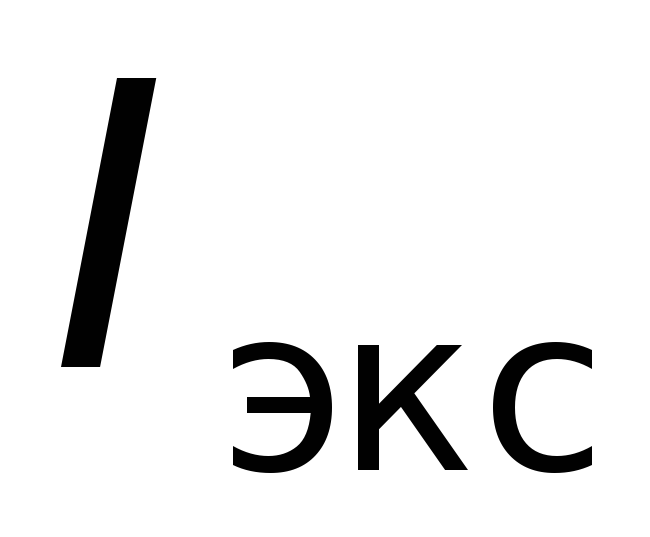и .

7. По предложению преподавателя повторить эксперимент, изменив массу груза 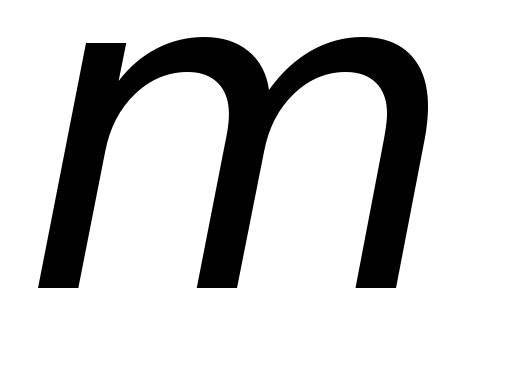или расстояние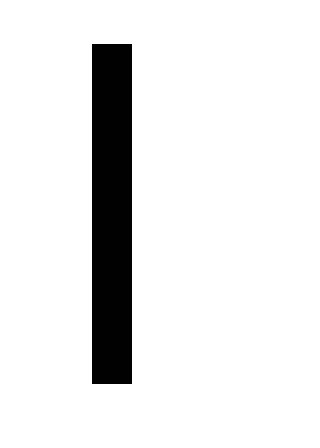, или то и другое одновременно.

Величины, считающиеся известными в данной работе:

= (0,00210,0001) кгм²,= (200,00,1) г,

= (62,00,1) г,= (27,00,5) см.

Контрольные вопросы

1. Дайте определение момента инерции тела и поясните его физический смысл. Напишите формулу для теоретического расчета момента инерции маятника.

2. Дайте определение момента силы относительно оси. Выведите формулу для расчета момента силы в данной работе.

3. Поясните смысл углового ускорения. Как оно направлено? В каких единицах измеряется? Как находят угловое ускорение в данной работе?

4. Запишите основной закон динамики вращательного движения. Выведите формулу (5.11) для экспериментального расчета момента инерции.

Литература

1. Савельев И. В. Курс физики. Т. 1. – М.: Наука, 1989. – С. 94–116.

2. Трофимова Т. И. Курс физики. – М.: Высш. шк., 2001. – С. 34–46.

Работа 1.6

Определение радиуса кривизны вогнутой поверхности методом катающегося шарика

Цель работы: определить радиус кривизны поверхности зеркала.

Приборы и принадлежности:вогнутое зеркало, шарики, секундомер, микрометр.

Описание установки и метода измерений

На рис. 6.1 показано сечение сферического зеркала MLN плоскостью чертежа. L – наинизшая точка зеркала. Если шарик поместить в произвольную точку С, а затем отпустить, он будет совершать колебательное движение.

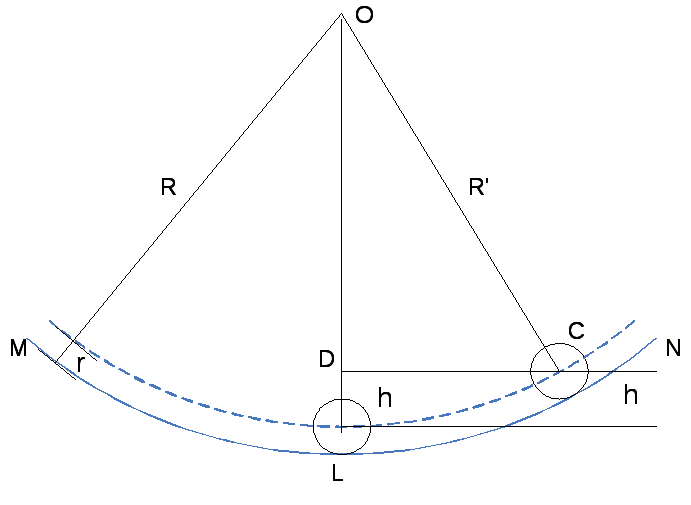
Рис. 6.1

Для нахождения радиуса кривизны зеркала Rиспользуют закон сохранения механической энергии. В точкеСмеханическая энергия шарика равна его потенциальной энергии,так как шарик неподвижен, а в точкеLмеханическая энергия шарика равна его кинетической энергии, которая слагается из кинетической энергии поступательного движенияи кинетической энергии вращательного движения.

Если пренебречь трением между шариком и поверхностью зеркала, то закон сохранения механической энергии для шарика будет иметь вид

, (6.1)

где – масса шарика,h– высота точкиСпо отношению к точкеL,–скорость поступательного движения шарика в точкеL, ω – угловая скорость вращательного движения шарика в той же точке,I– момент инерции шарика относительно оси, проходящей через его диаметр.

Учитывая, что момент инерции шарика , и, согласно (Т.5),(гдеr– радиус шарика), уравнение (6.1) можно преобразовать

. (6.2)

Высоту h, на которую поднимается центр масс шарика при его отклонении от положения равновесия, можно выразить через радиус кривизны поверхности, по которой движется центр масс шарика. Рассмотрим треугольникCOD, в котором ОС =R, ОD=R–h,DC=A(отрезокDCможно считать равным амплитуде колебаний шарикаА, так как при сравнительно малых отклонениях от положения равновесия хорда и стягиваемая ею дуга практически совпадают). Поскольку треугольник СОD прямоугольный, то для него можно записать теорему Пифагора

.

Если в последнем выражении раскрыть скобки и пренебречь величиной второго порядка малости (каковой является ), то получим, что

. (6.3)

Для нахождения скорости шарика необходимо знать уравнение его движения. Шарик совершает затухающие колебания, но при расчете радиуса кривизны не будет большой ошибкой считать, что он совершает незатухающие колебания, так как при малых коэффициентах затухания периоды затухающих и незатухающих колебаний различаются незначи-тельно. Итак, будем считать, что шарик совершает гармоническое колеба-тельное движение, описываемое уравнением

, (6.4)

где x– смещение шарика от положения равновесия в момент времениt,A– амплитуда колебаний шарика, ω –циклическая (или круговая) частота колебаний, связаннаяс периодом колебанийTсоотношением:

. (6.5)

Взяв первую производную от смещения (6.4) по времени, получим скорость шарика как функцию времени

. (6.6)

Из (6.6) следует, что максимальное значение скорость имеет при sint = 1,т. е. в точкеLскорость шарика равна

. (6.7)

Подставив (6.7) и (6.3) в (6.2), получим формулу для расчёта радиуса кривизны поверхности, по которой движется центр масс шарика

. (6.8)

Как видно из (6.8), для расчета Rнеобходимо знать только период колебаний шарика, который легко найти, измерив времяt, за которое шарик совершаетnколебаний:.

Из рис. 6.1 видно, что радиус кривизны поверхности зеркала R равен

. (6.9)