Порядок выполнения работы

1. Повернув цилиндр на небольшой угол, дать ему возможность колебаться. Для определения периода колебаний цилиндра 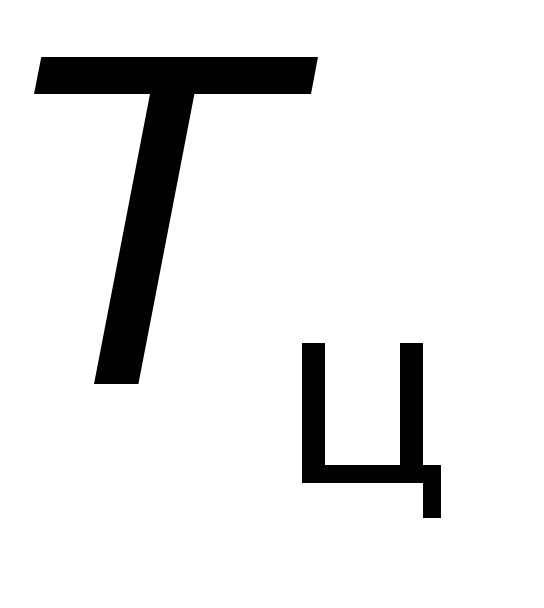3 раза определить время 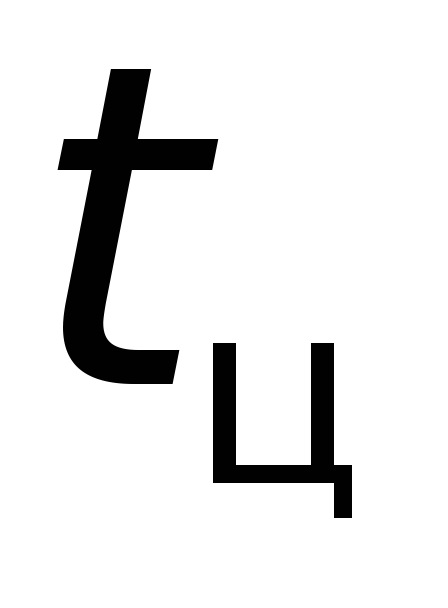10–15 его полных колебаний.

2. Поместить стержень в цилиндр так, чтобы его центр масс находился на оси вращения системы. Как и в предыдущем случае, определить 3 раза время 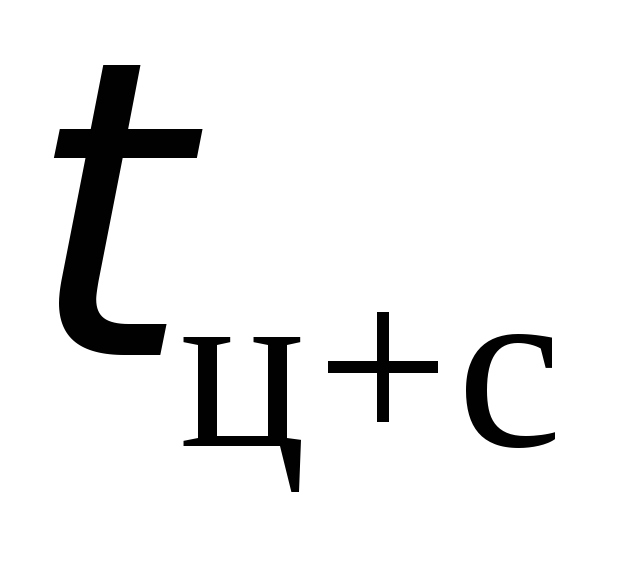10–15 полных колебаний.

3. Определить массу цилиндра m_ц и его диаметр d_ц.

4. Определить массу стержня m_с, его длину l_c и диаметр d_с.

5. По средним значениям периодов рассчитать экспериментальное значение момента инерции стержня.

6. Рассчитать теоретическое значение момента инерции стержня.

7. Результаты измерений и вычислений занести в таблицу

   №

   mц

   mс

   dц

   dс

   lc

   n

   tц

   Тц

   Тц

   tц+с

   Тц+с

   Тц+с

   Ic эксп

   Ic теор

   1

   2

   3

8. Рассчитать погрешности экспериментального и теоретического значений момента инерции. Сравнить полученные значения (с учетом их погрешностей)

Контрольные вопросы

1. Что такое момент инерции твёрдого тела? От чего он зависит? В каких единицах измеряется? Каков его физический смысл?

2. Чему равен момент силы, вызывающий крутильные колебания?

3. Запишите основной закон динамики вращательного движения в общем виде и конкретно для данной работы.

4. Выведите формулу периода крутильных колебаний.

5. Выведите формулу для экспериментального расчета момента инерции стержня.

6. Чем объясняется разница между теоретическим значением момента инерции стержня и значением, определённым опытным путём?

Литература

1. Савельев И. В. Курс физики. Т. 1. – М.: Наука, 1989. – С. 94–116.

2. Трофимова Т. И. Курс физики. – М.: Высш. шк., 2001. – С. 34–46.

Работа 1.4

Определение момента инерции физического маятника

Цель работы: определить моменты инерции физического маятника относительно разных осей вращения, предварительно определив положение его центра масс.

Приборы и принадлежности:физический маятник, секундомер, линейка.

Описание установки и метода измерений

Физическим маятником называется любое твёрдое тело, закрепленное на оси, не проходящей через его центр масс (рис. 4.1). При отклонении маятника от положения равновесия на некоторый угол сила тяжести ,приложенная в его центре массС, создает момент силы, возвращающий маятник в положение равновесия. Момент силы тяжести относительно оси , согласно (Т.8), равен

, (4.1)

где – расстояниеот оси вращения маятника О до его центра масс С, – плечо силы тяжести, знак "–" указывает на то, что момент силы возвращает тело в положение равновесия.

Рис. 4.1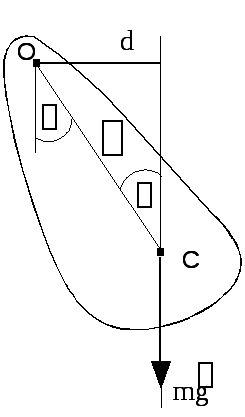

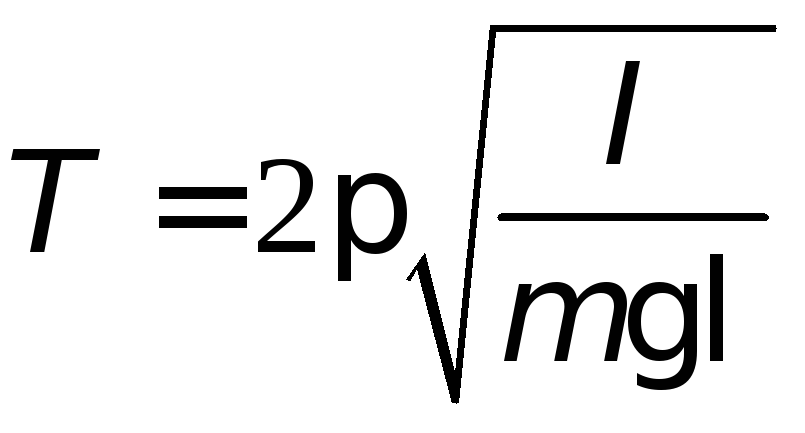Под действием возвращающего момента маятник совершает гармонические колебания с периодом, равным (вывод периода колебаний физического маятника дан в приложении к данной работе):

, (4.2)

где – период колебаний маятника, – момент инерции маятника относительно оси вращения О, – егомасса,– расстояние от центра масс до оси вращения, – ускорение свободного падения.

Формула (4.2.) позволяет легко найти момент инерции маятника, если известно, так как период колебаний можно измерить на опыте, определив времяt, за которое маятник совершаетnколебаний:

.

В данной работе физический маятник (рис. 4.2) представляет собой однородный стержень 1, на котором крепятся опорные призмы 2 и 3 равной массы и два одинаковых груза 4 и5. С помощью опорных призм маятник устанавливается на горизонтально закреплённую планку6.

Согласно формуле (4.2), момент инерции маятника относительно одной из осей (например, проходящей через опорную призму 2) равен

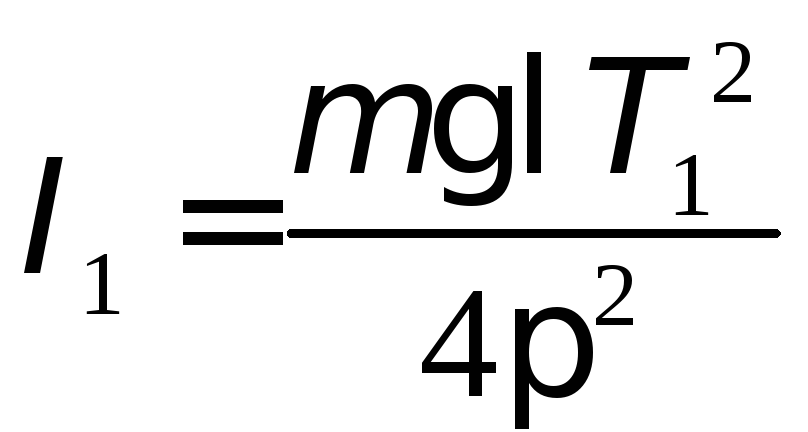. (4.3)

Но так как положение центра масс маятника неизвестно, поступают следующим образом. Маятник переворачивают. Относительно оси, проходящей через другую опорную призму, его момент инерции имеет вид

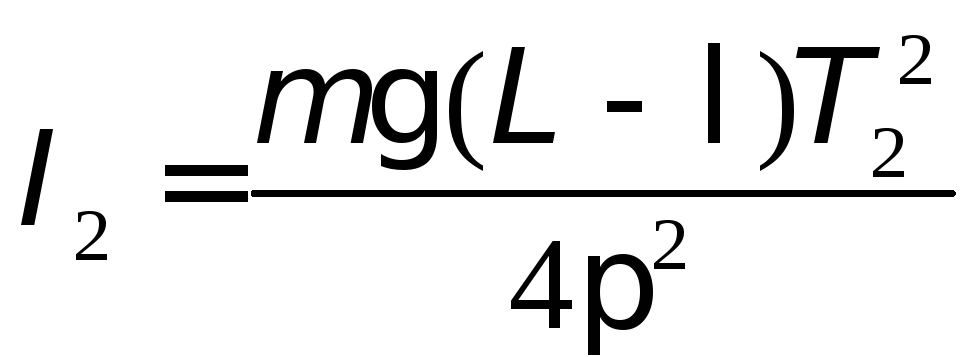, (4.4)

где L – расстояние между опорными призмами.

Уравнения (4.3) и (4.4) содержат три неизвестные величины. Для нахождения моментов инерции необходимы дополнительные уравнения. В качестве дополнительных уравнений записывают теорему Штейнера для и :

, (4.5)

, (4.6)

где – момент инерции стержня относительно оси, проходящей через центр масс стержня параллельно осям вращения.

Решив систему из четырёх уравнений (4.3), (4.4), (4.5) и (4.6), получают формулу для расчета положения центра масс маятника

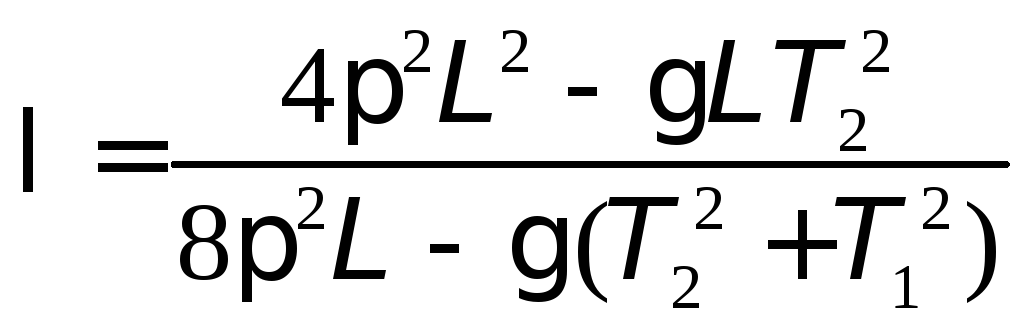. (4.7)

Вычислив , рассчитывают и .