
- •Динамика материальной точки и твердого тела
- •Оглавление
- •Введение
- •Расчет погрешностей и представление результатов измерений Типы погрешностей
- •Расчет погрешностей при прямых измерениях
- •Расчет погрешностей при косвенных измерениях
- •Как правильно округлить и записать результат
- •Как строить графики
- •Контрольные вопросы
- •Литература
- •Простейшие измерительные приборы Штангенциркуль
- •Микрометр
- •Вращение твердого тела вокруг неподвижной оси
- •Литература
- •Лабораторные работы
- •Определение плотности твердого тела
- •Краткая теория и описание метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Исследование основного закона динамики вращательного движения с помощью маятника обербека
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение момента инерции махового колеса
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение momehта инерции стержня методом крутильных колебаний
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение момента инерции физического маятника
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Приложение (вывод периода колебаний физического маятника)
- •Литература
- •Исследование основного закона динамики вращательного движения с помощью маятника обербека
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение радиуса кривизны вогнутой поверхности методом катающегося шарика
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Изучение удара шаров
- •Краткая теория
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение момента инерции тела и момента сил трения в подшипнике
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Изучение прецессионного движения гироскопа
- •Описание установки и метода измерений
- •Из рис. 9.2 следует, что
- •Порядок выполнения работы
- •Контрольные вопросы
- •Определение ускорения свободного падения с помощью математического маятника Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Определение ускорения свободного падения с помощью физического маятника Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Работа 1.11 изучение основного закона динамики вращательного движения с помощью маятника обербека
- •Описание установки и метода измерений
- •Основной закон динамики для вращательного движения в данной работе удобно записать в виде
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение скорости полета пули с помощью баллистического крутильного маятника
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение коэффициентов трения скольжения и трения качения с помощью наклонного маятника
- •Краткая теория
- •Трение скольжения
- •Трение качения
- •Описание установки и метода измерений
- •Часть 1 Определение коэффициента трения скольжения
- •Часть 2 Определение коэффициента трения качения
- •Контрольные вопросы
- •Литература
- •Изучение зависимости момента инерции тела от распределения его массы относительно оси вращения
- •Свободные оси вращения. Главные оси инерции
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •690059, Владивосток, ул. Верхнепортовая, 50а
Порядок выполнения работы
1. Передвигая грузы Свдоль стержней, добиться безразличного равнове-сия маятника.
2. Измерить диаметр шкива и рассчитать его радиус R.
3. Определить высоту падения грузов h.
4. Найти массу груза
![]() ,
уравновешивающего момент силы трения.
,
уравновешивающего момент силы трения.
5. Поместив на платформу груз массой m, определить время его падения не менее 3-х раз.
6. Указанное в п. 5 проделать тремя грузами (указанными преподавателем).
7. Данные измерений занести в таблицу
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
| |||
|
3 |
|
|
|
|
|
|
|
|
8. Предварительно убедившись, что
![]() <<
<<![]() ,
рассчитать для каждого из грузоввращающий момент по формуле (1.8).
,
рассчитать для каждого из грузоввращающий момент по формуле (1.8).
9. Рассчитать угловое ускорение маятника Обербека по формуле (1.9).
10. Убедиться в выполнении равенств (1.2).
11. Построить график зависимости углового
ускорения маятника
![]() от вращающего момента
от вращающего момента![]() .
.
12. Определить момент инерции маятника с помощью графика и сравнить полученное значение со средним значением, рассчитанным по формуле (1.1).
13. По указанию преподавателя оценить
погрешности измерения величин
![]() и
и![]() и показать их на графике.
и показать их на графике.
Контрольные вопросы
Дайте определение момента инерции тела. Поясните его физический смысл. В каких единицах измеряется момент инерции? Как можно изменить момент инерции маятника в данной работе?
Чему равен момент силы относительно неподвижной оси? Что он характеризует? В каких единицах измеряется?
Что называется плечом силы?
Что такое угловая скорость, угловое ускорение? Каков смысл этих величин? В каких единицах они измеряются?
Какие направления имеют в данной работе моменты сил трения и натяжения, угловая скорость, угловое ускорение?
Напишите основной закон динамики для поступательного и вращательного движений.
Выведите расчётные формулы для вращающего момента (1.7) и углового ускорения (1.8).
Литература
Савельев И. В. Курс физики. Т. 1. – М.: Наука, 1989. – С. 94–116.
Трофимова Т. И. Курс физики. – М.: Высш. шк., 2001. – С. 34–46.
Зисман Г. А., Тодес О. М. Курс обшей физики. Т. 1. – М.: Наука, 1972. – С. 59–70.
Работа 1.2
Определение момента инерции махового колеса
Цель работы: вычислить момент инерции махового колеса с помощью падающего груза.
Приборы и принадлежности: маховое колесо, набор грузов, масштабная линейка, штангенциркуль, секундомер.
Описание установки и метода измерений
Маховое колесо Ми шкив радиусаRнасажены на единую осьО(рис. 1.2). На
шкив навит шнурок, к которому прикреплён
груз массой![]() .
Грузу сообщают потенциальную энергию,
подняв его на высоту
.
Грузу сообщают потенциальную энергию,
подняв его на высоту
![]() по отношению к некоторому уровню, высота
которого принята за ноль. При падении
груза его потенциальная энергия
по отношению к некоторому уровню, высота
которого принята за ноль. При падении
груза его потенциальная энергия
![]() переходит в кинетическую энергию
поступательного движения груза
переходит в кинетическую энергию
поступательного движения груза![]() и кинетическую энергию вращательного
движения маховика
и кинетическую энергию вращательного
движения маховика
![]() ,
а также расходуется на преодоление сил
трения в подшипнике. Таким образом,
закон сохранения механической энергии
для данной системы имеет вид
,
а также расходуется на преодоление сил
трения в подшипнике. Таким образом,
закон сохранения механической энергии
для данной системы имеет вид
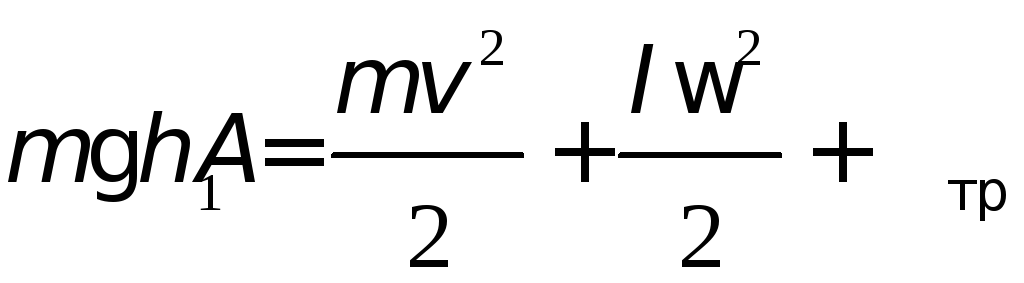 ,(2.1)
,(2.1)
где
![]() – ускорение свободного падения,
– ускорение свободного падения,![]() – высота, на которую поднят груз,
– высота, на которую поднят груз,![]() –
скорость груза в нижней точке падения,
–
скорость груза в нижней точке падения,
![]() – угловая скорость маховика в тот же
момент времени,
– угловая скорость маховика в тот же
момент времени,![]() –
момент инерции махового колеса,
–
момент инерции махового колеса,
![]() –
работа по преодолению сил трения в
подшипнике при движении груза вниз.
–
работа по преодолению сил трения в
подшипнике при движении груза вниз.
С помощью
уравнения (2.1) можно экспериментально
определить момент инерции махового
колеса,
если известны остальные величины:
![]() ,
,
![]() ,
,![]() ,
,![]() и
и![]() .
.
Рис. 2.1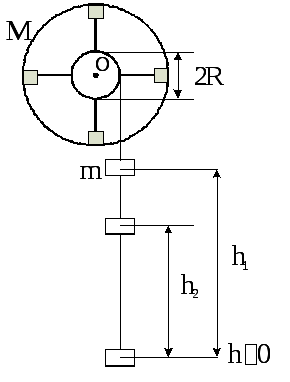
![]() ,
(2.2)
,
(2.2)
где
![]() – сила трения в подшипнике, которуюможно найти, исходя
из следующихсоображений.
Если колесо не остановить, то оно,
вращаясь по инерции, поднимет груз наменьшую высоту
– сила трения в подшипнике, которуюможно найти, исходя
из следующихсоображений.
Если колесо не остановить, то оно,
вращаясь по инерции, поднимет груз наменьшую высоту
![]() .
Работа силы трения навсем
пути
.
Работа силы трения навсем
пути
![]() равна разности
потенциальных энергий груза в
конечном и начальном положениях, т. е.
равна разности
потенциальных энергий груза в
конечном и начальном положениях, т. е.
![]() ,
,
откуда
![]() .
(2.3)
.
(2.3)
Подставив (2.3) в (2.2), получим формулу для расчета работы силы трения при движении груза вниз
![]() .
(2.4)
.
(2.4)
На груз действуют постоянные силы, поэтому его движение является равноускоренным и описывается уравнениями
![]() и
и![]() .
.
Исключив из этих уравнений ускорение, получим выражение для линейной скорости груза в нижней точке
![]() .
(2.5)
.
(2.5)
Нить, на которой
подвешен груз, практически нерастяжима,
следовательно,
линейная скорость точек обода шкива
равна скорости груза. И угловуюскорость махового колеса можно получить,
используя соотношение между линейной
и угловой скоростями (Т.5)![]() .
В момент, когда груз находится в нижней
точке траектории, угловая скорость
махового колеса равна
.
В момент, когда груз находится в нижней
точке траектории, угловая скорость
махового колеса равна
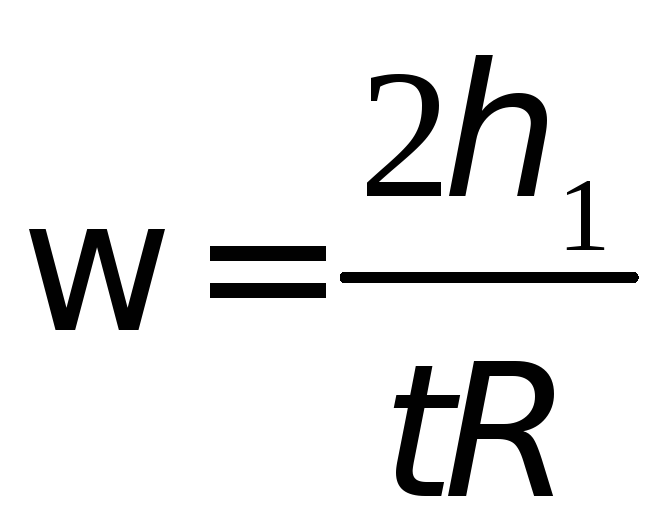 ,
(2.6)
,
(2.6)
где t – время падения груза с высоты h1.
Подставив выражение (2.4), а также выражения (2.5) и (2.6) в (2.1), получим формулу для вычисления момента инерции махового колеса в данной работе
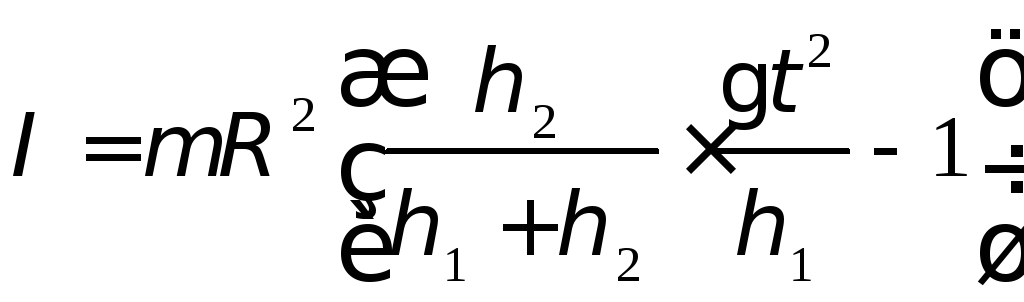 .
(2.7)
.
(2.7)
