Вопрос 3. Средние и предельные ошибки выборки при различных способах отбора. Средние и предельные ошибки малой выборки.

В результате выборочного наблюдения возникают случайные ошибки репрезентативности, связанные с разностью показателей генеральной совокупности и выборочной совокупности.

Для распространения результатов наблюдения за выборочной совокупностью на совокупность генеральную необходимо знать размеры ошибки. Для этого в математической статистике есть ряд приемов.

При этом сопоставляются средние и доли генеральной и выборочной совокупности.

Основная проблема здесь заключается в том, что на основе одной генеральной совокупности может быть образовано множество выборочных совокупностей. Например, если в генеральной совокупности 1000 единиц, в выборочной – 100, то вариантов выборочных совокупностей:

В каждой из этих совокупностей будут свои ошибки. Поэтому приходится оперировать не конкретными ошибками, а средними ошибками:

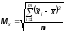
m – число выборок, 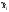– среднее значение признака вi-ой выборке.

В математической статистике средняя ошибка выборки определяется по формуле:

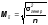
n – размер выборки.

Это формула используется для расчета средней ошибки для повторной выборки.

Если же отбор бесповторный, то используется формула:

N – размер генеральной совокупности, n – размер выборочной совокупности.

Средняя ошибка для доли:

повторная выборка:

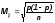
бесповторная выборка:

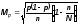
p – доля единиц, которые обладают данным признаком.

Однако по этим формулам считать в лоб нельзя, так как нужно знать дисперсию генеральной совокупности. Между дисперсиями генеральной и выборочной совокупности есть следующее соотношение:

При размере выборки 20 и более единиц соотношение 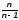будет близко к единицы, и потому оно не учитывается. Тогда вместо дисперсии генеральной совокупностиберется дисперсия выборочной совокупности.

Это всё были формулы для собственно случайного отбора. Если же отбор механический, то используются такие же формулы, поскольку в курсе “Математическая статистика” доказывается, что ошибка при механическом отборе не больше, чем при собственно случайном отборе.

При типическом отборе применяются следующие формулы.

повторная:

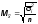
бесповторная:

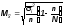
где .

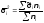n_i – размер i-ой группы, 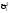– дисперсия вi-ой группе, 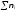– общий размер выборки.

Соответственно для доли при типическом бесповторном отборе:

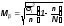
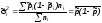
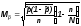
(для повторного отбора коэффициент 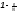не учитывается)

При серийном отборе используется межсерийная выборочная дисперсия. Считаем по формуле:

где s – число отобранных серий в выборочной совокупности, S – число серий в генеральной совокупности, 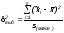– межсерийная выборочная дисперсия.

Для доли:

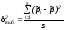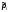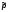, где – доля единиц, обладающих данным признаком, вi-ой, – доля единиц, обладающих признаком, в выборке.

В каждом конкретном наблюдении ошибка может оказаться больше или меньше средней. Именно поэтому оперируют не средней, а предельной ошибкой выборки (определяют пределы, за которые ошибка выйти не может).

При определении предельной ошибки выборки делается допущение, что выборочные средние распределены нормально относительно генеральной средней. Тогда можно использовать стандартную интегральную функцию нормального распределения:

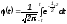
t – нормированное отклонение, 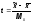, гдеM_x – средняя ошибка выборки.

Имеем: .

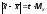Разность, стоящая в левой части равенства, – это предельная ошибка выборки, т.е.

.

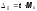Или для доли:

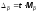
Например, t=1, тогда предельная ошибка не превысит однократной средней ошибки. Из интегрального уравнения Лапласа 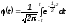находим: приt=1 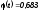. Это означает, что из 1000 в 683 случаях ошибка не выйдет за пределы выборки.

Основные значения t и 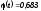таковы:

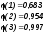
От чего зависит предельная ошибка выборки?

Как нам известно, .

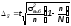Значит, предельная ошибка зависит от:

1. от размера выборочной дисперсии

2. от размера выборки

3. от того, с какой вероятностью мы хотим гарантировать ошибку выборки.

Манипулируя вторым и третьим параметрами, можно добиваться любых целей.

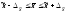
Это доверительный интервал, в котором находится генеральная средняя.

Так же и для доли:

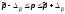
Все эти формулы применяются при достаточно большой выборке (более нескольких сот единиц). Однако зачастую это невозможно (например, контроль качества деталей). Тогда используется малая выборка – выборка менее 20 единиц.

В расчете средней и предельной ошибок малой выборки есть ряд особенностей.

Так, .

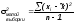Соответственно рассчитывается средняя и предельная ошибка малой выборки.

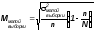
Что касается предельной ошибки, то

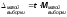
Однако, t (коэффициент доверия) распределяется не в соответствии с нормальным распределением (как было при большой выборке), а в соответствии с распределением Стьюдента. Особенностью распределения Стьюдента является то, что значения функции распределения зависят не только от t, но и от размера выборки:

n t	5	10	15
2	0,884	0,923	0,935
3	0,96	0,985	0,99

В экономике малую выборку лучше не использовать!!!