6

Лекция 12.

Тема 4. Элементы высшей алгебры Множества и действия сними.

Определение: совокупность однородных элементов (объединенных каким либо свойством) произвольной природы называется множеством. Множества: целых чисел, комплексных чисел, вещественных чисел, городов, студентов, …

Операции с множествами.

1. Два множества называются равными, если они составлены из одних и тех же элементов. При этом совпадающие элементы в множестве рассматриваются как один элемент.

A={1,3,5} B={1,3,5,3,1} → A=B

2. Говорят, что множество А включается в множество В если из того, что х принадлежит А (х  А) следует, что х  В. При этом говорят, что А это подмножество В. Записывают АВ (А включается в В) или ВА.

3. Умножением (пересечением) множеств А и В называется множество, состоящее из элементов принадлежащих обоим множествам, и обозначается АВ.

A={1,3,5,7,9,10} В={1,2,3,4,5,6,7} АВ={1,3,5,7}

4. Суммой (объединением) множеств А и В называется множество, состоящее из элементов принадлежащих одному или другому множеству, и обозначается АВ.

А={1,5,9} B={1,2,5,10} АВ={1,2,5,9,10}

4. Разностью множеств А и В называется множество, состоящее из элементов принадлежащих А и не принадлежащих В, и обозначается А\В.

А={1,5,9} B={1,2,5,10} А\В={9}

Пример числовых множеств и их обозначения:

N={1,2,3,…,n,…,∞}- множество натуральных чисел;

Z={-∞,…,-2,-1,0,1,2,…, ∞}- множество целых чисел:

Q={p/q; p,q є Z; q≠0}∞}- множество рациональных чисел;

R₁={,,,, , e, π,…} – множество иррациональных чисел;

R=NZQ R₁ – множество действительных (вещественных чисел) чисел;

С={ a+ib ; i=; a,b  R}– множество комплексных чисел.

Определение: Интервалом называется множество чисел (а,в)→{x} таких, что а<x<b числа а,вєR → { (Для всех)x; а<x<b ; а,вєR }

Определение: Отрезком называется множество чисел [а,в]→{x} таких, что а≤x≤b числа а,вєR → {x; а≤x≤b ; а,вєR }

Определение: Эпсилон ε окрестностью или просто окрестностью точки х₀ называется множество чисел О_ε=(x;х₀- ε <x<x₀+ ε ).

Линейное (векторное) пространство.

Как известно, линейные операции (сложение, вычитание, умножение на число) определены по-своему для каждого множества (числа, многочлены, направленные отрезки, матрицы). Сами операции различны, но их свойства одинаковы.

Эта общность свойств позволяет обобщить понятие линейных операций для любых множеств вне зависимости от того, что это за множества (числа, матрицы и т.д.).

Для того, чтобы дать определение линейного (векторного) пространства рассмотрим некоторое множество L действительных элементов, для которых определены операции сложения и умножения на число.

Эти операции обладают свойствами:

1. 1) Коммутативность + = +

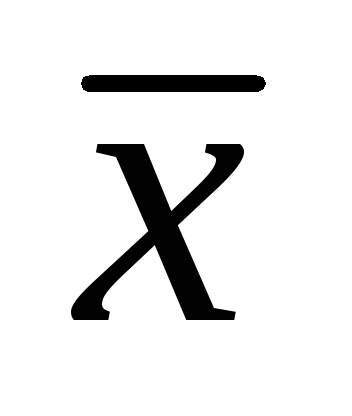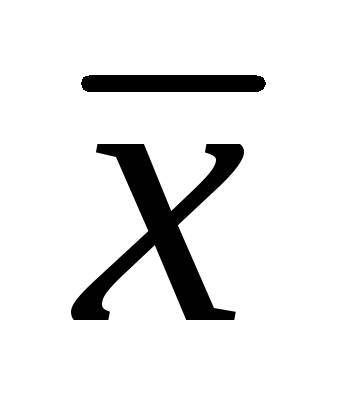
2. 2) Ассоциативность (+) + = + (+)

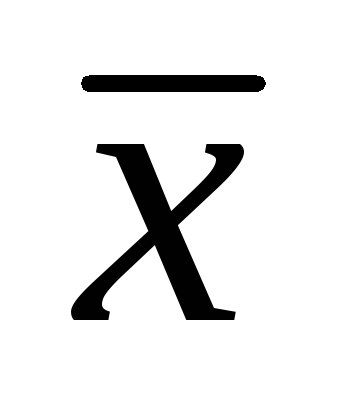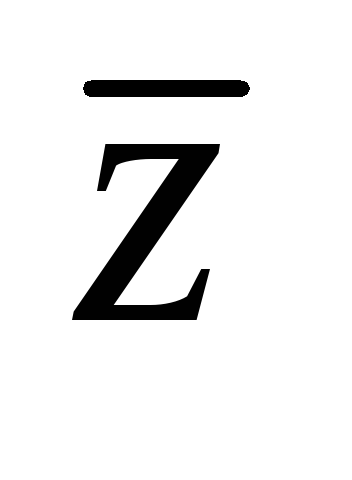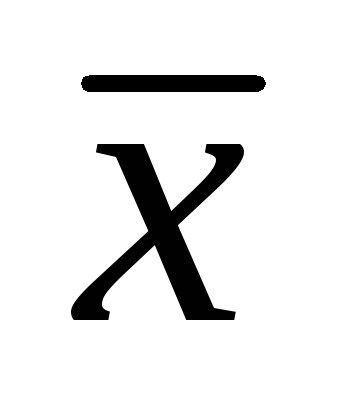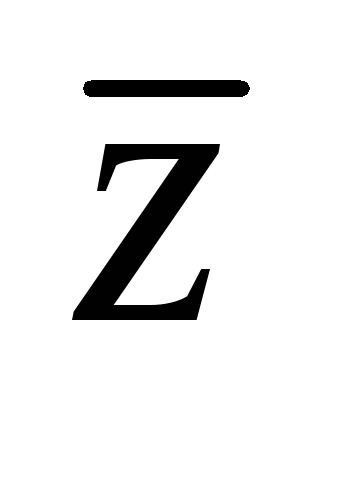3)Существует такой нулевой вектор , что +=для  L

4)  (Для всех)  L существует вектор = -, такой, что +=

5)1 =

6) () = ()

7) Распределительный закон ( + ) = + 

8) (+) = + 

Определение: Множество L называется линейным (векторным) пространством, а его элементы называются векторами.

Важно не путать приведенное понятие вектора с понятием вектора как направленного отрезка на плоскости или в пространстве. Направленные отрезки являются всего лишь частным случаем элементов линейного (векторного) пространства. Линейное (векторное) пространство – понятие более широкое. Примерами таких пространств могут служить множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д.

Если операции сложения и умножения на число определены для действительных элементов, то линейное (векторное) пространство является вещественным пространством, если для комплексных элементов – комплексным пространством.