
Лекции по математике (ТХФИ11) / 1 семестр_Лекция №11
.doc
Лекция 11.
Уравнение поверхности в пространстве.
Определение. Уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
F(x,y,z)=0
Поверхности второго порядка.
Определение. Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка т.е. содержащими квадраты x,y,z.
Цилиндрические поверхности.
Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:
-
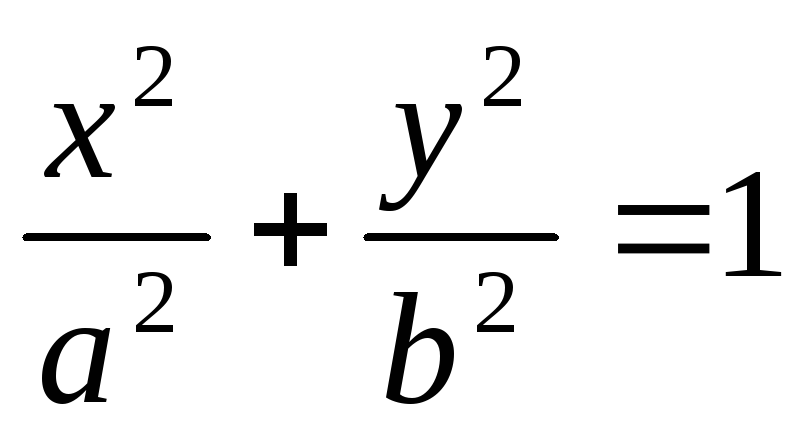 -
эллиптический
цилиндр.
-
эллиптический
цилиндр.

2)
![]() - гиперболический
цилиндр.
- гиперболический
цилиндр.
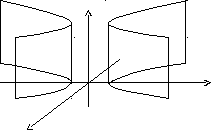
-
x2 = 2py – параболический цилиндр.
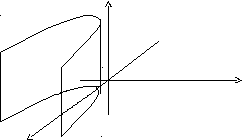
Поверхности вращения.
Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d.
Если уравнение поверхности в прямоугольной системе координат имеет вид:
F(x2 + y2, z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz.
Аналогично: F(x2 + z2, y) = 0 – поверхность вращения с осью вращения Оу,
F(z2 + y2, x) = 0 – поверхность вращения с осью вращения Ох.
Запишем уравнения поверхностей вращения для некоторых частных случаев:
-
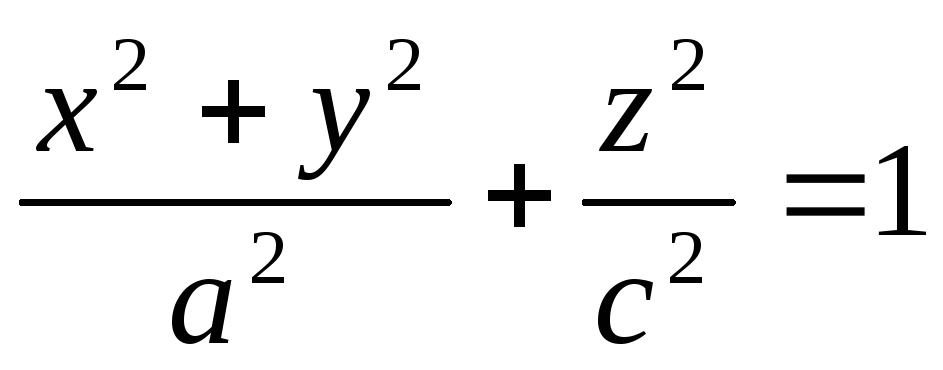 -
эллипсоид
вращения
-
эллипсоид
вращения -
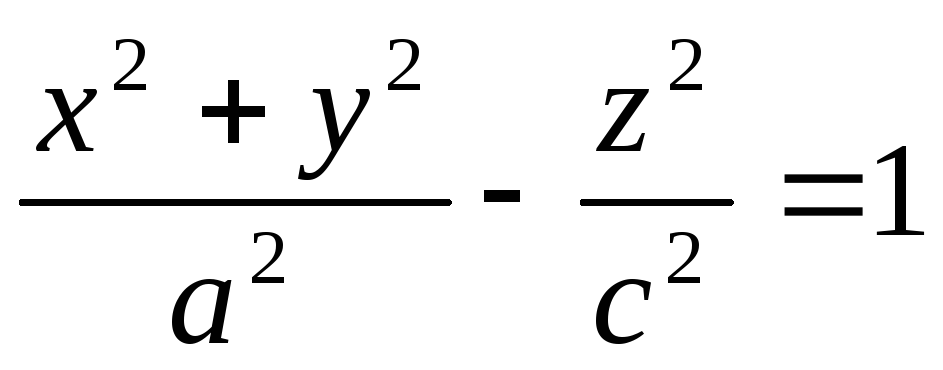 -
однополостный
гиперболоид вращения
-
однополостный
гиперболоид вращения -
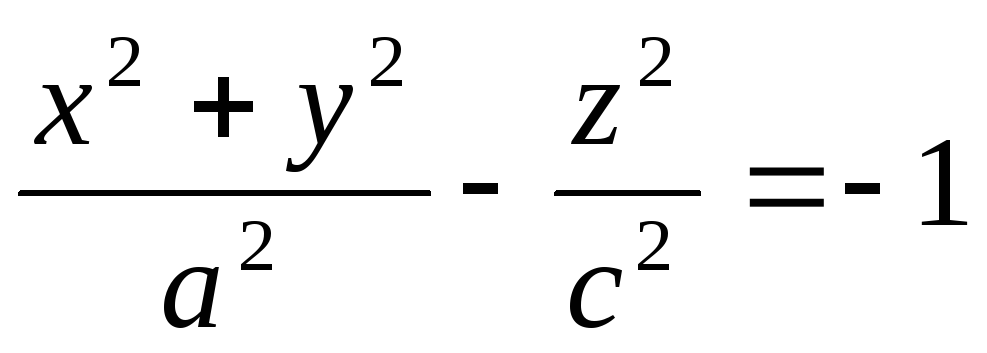 -
двуполостный
гиперболоид вращения
-
двуполостный
гиперболоид вращения
-
 -
параболоид
вращения
-
параболоид
вращения
Аналогично могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси Ох или Оу.
Однако, перечисленные выше поверхности являются всего лишь частными случаями поверхностей второго порядка общего вида, некоторые типы которых рассмотрены ниже:
Сфера:
![]()
Трехосный
эллипсоид:
![]()
В сечении эллипсоида плоскостями, параллельными координатным плоскостям, получаются эллипсы с различными осями.
Однополостный
гиперболоид:
![]()

Двуполостный
гиперболоид:
![]()

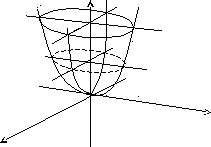
Эллиптический
параболоид:
![]()
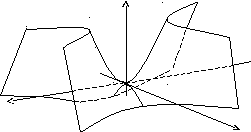
Гиперболический
параболоид:
![]()
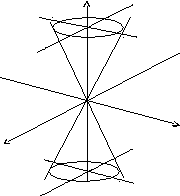
Конус второго
порядка:
![]()
Основным методом исследования формы поверхности в пространстве является метод сечения плоскостями параллельными координатным плоскостям.
x=h – плоскость | | плоскости Оyz(x=0), смещенная вдоль оси х на h;
y=h – плоскость | | плоскости Оxz (y=0), смещенная вдоль оси y на h;;
z=h – плоскость | | плоскости Оxy (z=0), смещенная вдоль оси z на h;;
Для получения уравнения линии а сечении поверхности плоскостью необходимо подставит уравнение секущей плоскости в уравнение поверхности и построит на бумаге в декартово системе координат соответствующую линию. Меняя параметр h можно получить семейство линий, которые и представят форму поверхности.
Например,
если подставить в уравнение трехосного
эллипсоида
![]()
уравнение
x=h,
то в плоскости Оyz
получим эллипсы
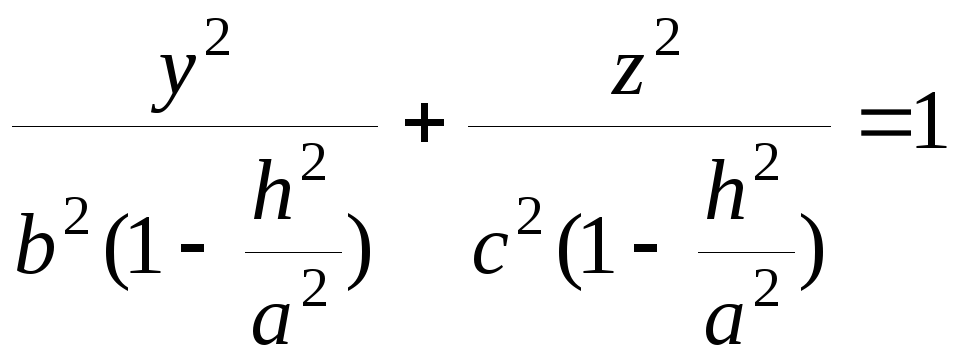 .
При увеличении h
размеры эллипсов будут уменьшаться.
Далее сечем плоскостями y=h
и z=h.
Получим рисунок поверхности.
.
При увеличении h
размеры эллипсов будут уменьшаться.
Далее сечем плоскостями y=h
и z=h.
Получим рисунок поверхности.
Цилиндрическая и сферическая системы координат.
Как и на плоскости, в пространстве положение любой точки может быть определено тремя координатами в различных системах координат, отличных от декартовой прямоугольной системы. Цилиндрическая и сферическая системы координат являются обобщением для пространства полярной системы координат, которая была подробно рассмотрена ранее.
Введем
в пространстве точку О и луч l,
выходящий из точки О, а также вектор
![]() .
Через точку О можно провести единственную
плоскость, перпендикулярную вектору
нормали
.
Через точку О можно провести единственную
плоскость, перпендикулярную вектору
нормали
![]() .
.
Для введения соответствия между цилиндрической, сферической и декартовой прямоугольной системами координат точку О совмещают с началом декартовой прямоугольной системы координат, луч l – с положительным направлением оси х, вектор нормали – с осью z.
Цилиндрическая и сферическая системы координат используются в тех случаях, когда уравнение кривой или поверхности в декартовой прямоугольной системе координат выглядят достаточно сложно, и операции с таким уравнением представляются трудоемкими.
Представление уравнений в цилиндрической и сферической системе позволяет значительно упростить вычисления, что будет показано далее.
 z
z
М
h
O x
r
M1
y
![]() ОМ1
= r;
MM1
= h;
ОМ1
= r;
MM1
= h;
Если из точки М опустить перпендикуляр ММ1 на плоскость, то точка М1 будет иметь на плоскости полярные координаты (r, ).
Определение. Цилиндрическими координатами точки М называются числа (r, , h), которые определяют положение точки М в пространстве.
Определение. Сферическими координатами точки М называются числа (,,), где - угол между и нормалью.
Связь цилиндрической и декартовой прямоугольной
системами координат.
Аналогично полярной системе координат на плоскости можно записать соотношения, связывающие между собой различные системы координат в пространстве. Для цилиндрической и декартовой прямоугольной систем эти соотношения имеют вид:
h
= z; x = rcos;
y = rsin;
cos
=
![]() ;
sin
=
;
sin
=
![]() .
.
Связь сферической системы координат с
декартовой прямоугольной.
В случае сферической системы координат соотношения имеют вид:
![]()
![]()
