13. Классификация точек разрыва функции одной переменной

Точка аназываетсяточкой разрыва функции, если в этой точке нарушается условие непрерывности, т.е. или 1)не определена в точкеа, или 2)существует, но не равен, или 3)не существует.

Определение 13.1.Точка разрываафункцииназываетсяточкой разрыва первого рода этой функции, если в этой точке существуют оба односторонних пределаи. В частности, при условии=точка разрыва первого рода называетсяточкой устранимого разрыва.

Разность 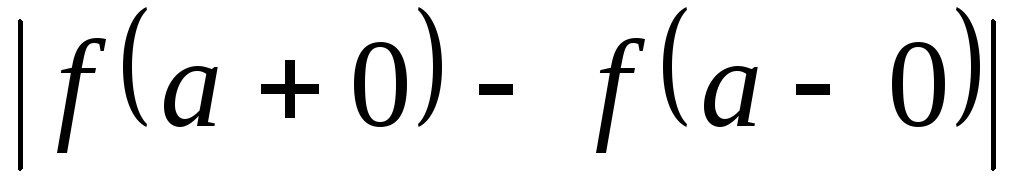называетсяскачкомфункциив точкеа. В случае устранимого разрыва скачок равен нулю. Если же разрыв первого рода неустраним, то скачок отличен от нуля. В случае точки устранимого разрыва предел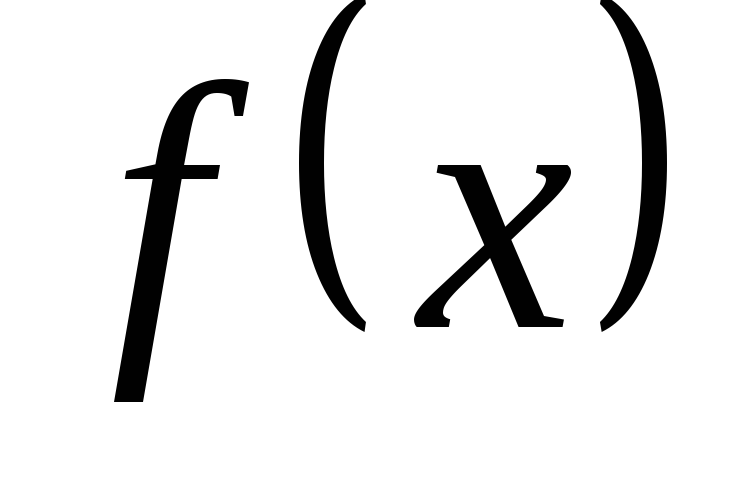в этой точке существует, но либо не равен, либов точкеа не определена. Если же в точке разрыва первого рода разрыв неустраним, то в этой точке пределне существует.

Определение 13.2.Точка разрываафункции называется точкой разрыва второго рода, если в этой точке хотя бы один из односторонних пределов не существует или равен бесконечности.

Пример.1). Точках=0является точкой разрыва, так как в этой точке функция не определена. В силу первого замечательного предела. Отсюда по теореме 5.2. в точкех=0функция имеет оба односторонних предела, равных между собой. Значит,х=0есть точка устранимого разрыва. Этот разрыв можно устранить, если функциюв точкех=0доопределить, положив. (см. рис. 13.1)

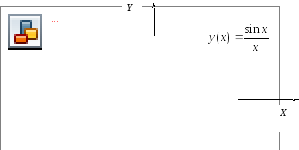
Рис. 13.1

2) .

Вычислим односторонние пределы этой функции в точке :,. Обаодносторонних предела существуют, значит х=0 есть точка разрыва первого рода. Так как пределы неравны, то устранить разрыв нельзя (см. рис.13.2)

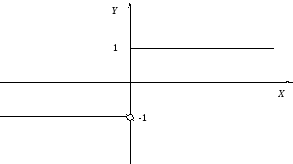
Рис. 13.2

Рис. 13.3

3

). Поскольку в точкех=0оба односторонних предела не существуют, точках=0является точкой разрыва второго рода (см. рис.13.3).