Лекции. Математика / Сем1_лекция 4

Линии второго порядка

Линиями второго порядка называются линии, описываемые уравнениями второй степени (второго порядка) относительно текущих координат. Самый общий вид уравнения второго порядка

Ax²+By²+Dxy+Ex+Fy+H=0. (2.13)

Окружностью называется геометрическое место точек равноудаленных от данной точки С, называемой центром окружности.

Уравнение окружности радиуса R с центром в точке C(a,b) имеет вид

(2.14)

Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных фиксированных точек F₁ и F₂ , называемых фокусами эллипса, есть величина постоянная (большая, чем расстояние между фокусами).

Таким образом, в соответствии с приведенным определением (рис.19), , , , где a и c - заданные параметры эллипса (линии L).

Рис. 19

Каноническое уравнение эллипса, построенного по приведенному определению, имеет вид

, (2.15)

где откуда следует, что .

У эллипса а - большая полуось, b - малая полуось, с – полуфокусное расстояние, - левый фокальный радиус, - правый фокальный радиус. Отношение полуфокусного расстояния к большой полуоси эллипса называется эксцентриситетом эллипса - Т.к. для эллипса c<a , то <1 .

В случае если с=0 , то b²=a² и уравнение эллипса (2.15) вырождается в уравнение окружности радиуса - a с центром в начале координат: x²+y²=a². Т.о., окружность есть эллипс нулевого эксцентриситета, и эксцентриситет эллипса является показателем степени отклонения эллипса от окружности.

Прямые, параллельные малой оси эллипса и отстоящие от нее на расстоянии , называются директрисами эллипса (рис. 20).

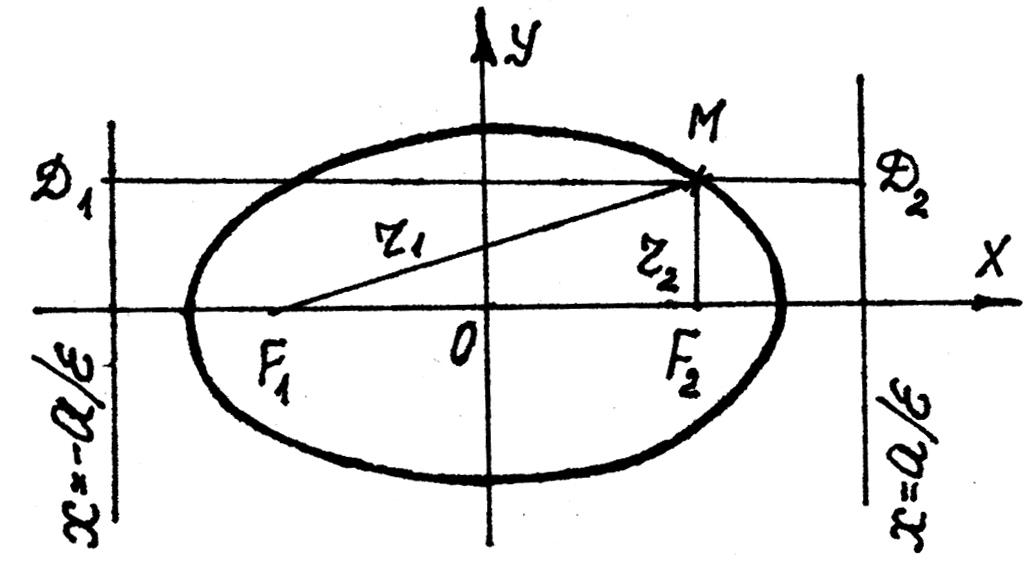
Рис. 20

- правая директриса, - левая директриса. Фокальные радиусы текущей точки и расстояния от нее до соответствующих директрис связывают следующие соотношения где и .

Гиперболой называется геометрическое место точек разность расстояний, которых до двух данных точек F₁ и F₂ , называемых фокусами гиперболы, взятая по модулю, есть величина постоянная (меньшая, чем расстояние между фокусами).

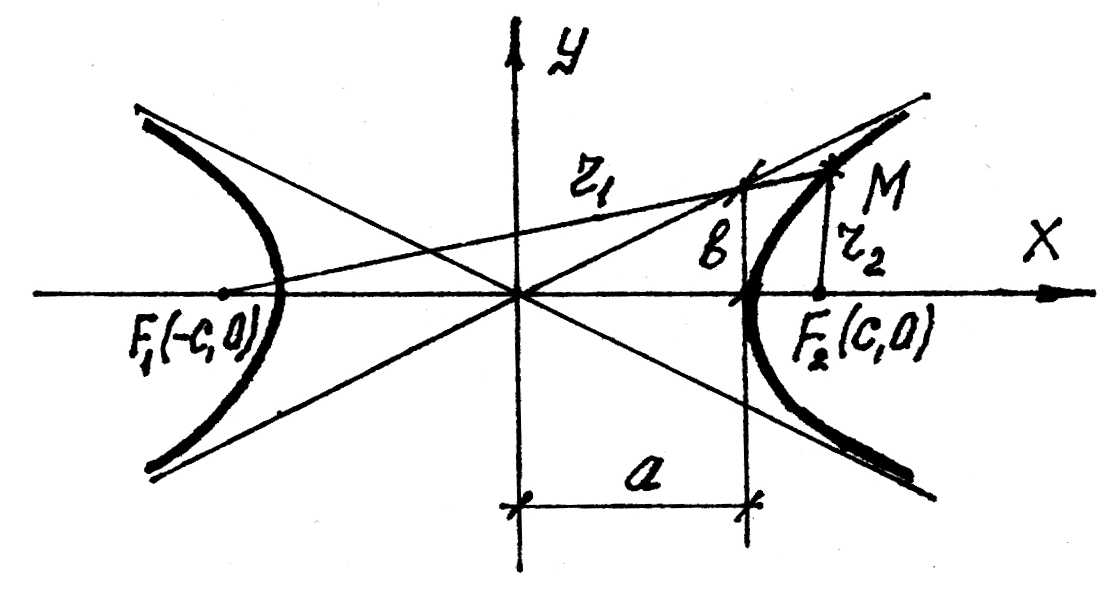Согласно определению (рис.21) , , 2a<2c, где a и c - заданные величины.

Рис. 21

Каноническое уравнение гиперболы, построенной по приведенному определению, имеет вид

, (2.16)

где .

У гиперболы a - действительная полуось, b - мнимая полуось, с - полуфокусное расстояние, и - соответственно левый и правый фокальные радиусы текущей точки, - эксцентриситет гиперболы. Поскольку для гиперболы c>a , то эксцентриситет гиперболы Прямые - асимптоты гиперболы. Прямые перпендикулярные действительной оси гиперболы и отстоящие от центра гиперболы на расстоянии называются директрисами гиперболы, их уравнения . Так как для гиперболы , то , и директрисы гиперболы расположены между вершинами гиперболы (рис. 22). Так же как и для эллипса здесь справедливы соотношения , где и - расстояния от текущей точки гиперболы до соответствующей директрисы.

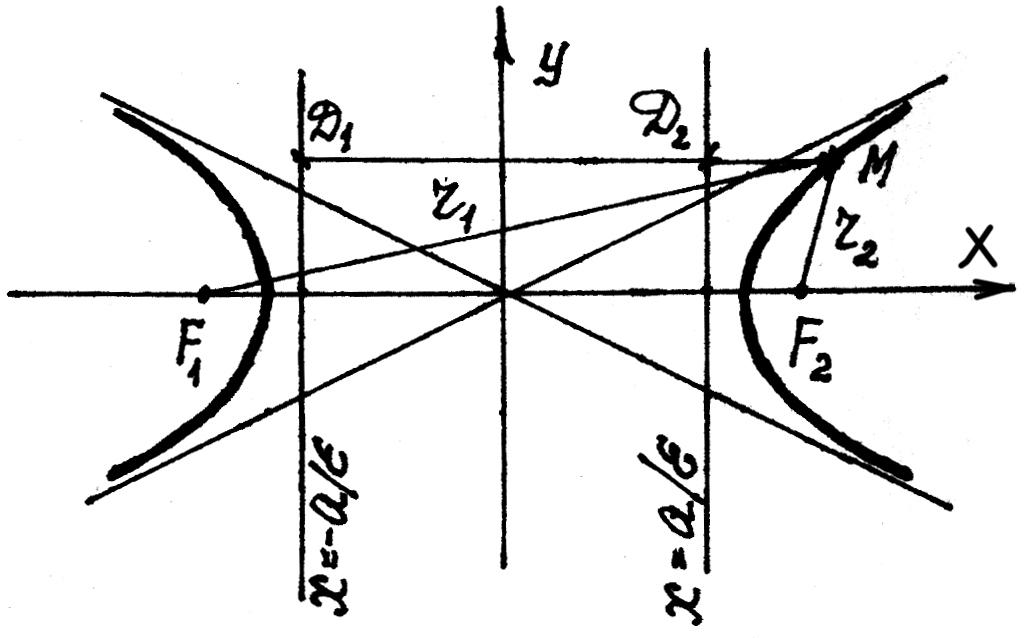
Рис. 22

Параболой называется геометрическое место точек равноудаленных от точки F - фокуса параболы и от прямой DD' – директрисы параболы, причем фокус не лежит на директрисе.

Из определения для любой точки M параболы . - заданная величина параметр параболы.

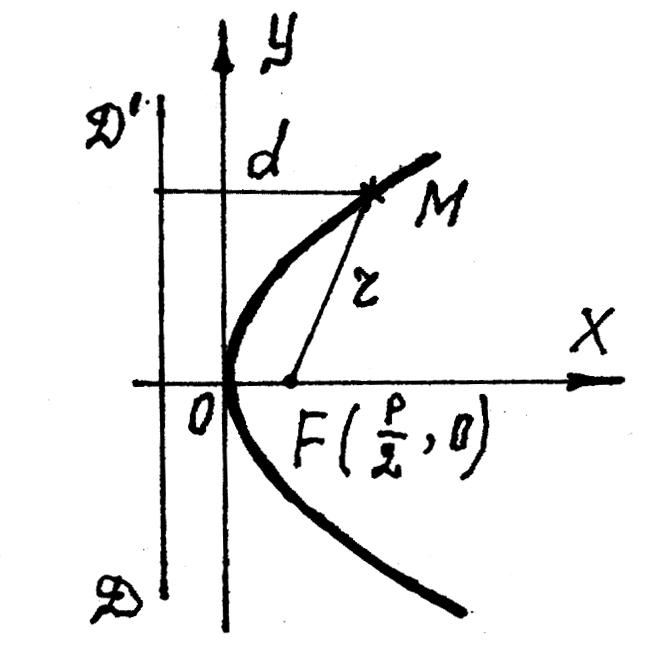Рис. 23

Каноническое уравнение параболы, построенной по определению и приведенной на рис. 23, имеет вид

. (2.17)

O(0,0) - вершина параболы. У рассматриваемой параболы можно выделить ветви: верхнюю и нижнюю. Если, так же как это ранее было у эллипса и у гиперболы, обозначить через эксцентриситет , то видим, что для параболы . Таким образом, для эллипса, гиперболы и параболы отношение фокального радиуса текущей точки к расстоянию ее до соответствующей директрисы есть эксцентриситет соответствующей кривой. При этом эксцентриситет эллипса , эксцентриситет гиперболы , а эксцентриситет параболы .

Нетрудно сообразить, что уравнению

(2.18)

соответствует парабола, приведенная на рис.24.

Уравнениям

(2.19)

и

(2.20)

соответствуют параболы, приведенные на рис. 25 и 26, осью симметрии которых является ось ординат.

Рис. 24 Рис. 25 Рис. 26

В курсе элементарной математики изучались гипербола и парабола. При этом гиперболе соответствовало уравнение обратно - пропорциональной зависимости y=k/x , параболе - уравнение . Свяжем эти понятия курса средней школы с понятиями, которые получили, изучая курс аналитической геометрии.

Уравнение конических сечений. Ранее было показано, что эллипс, гипербола и парабола – линии второго порядка. Эти линии называются коническими сечениями, поскольку лишь эти линии могут быть получены в сечении любого кругового конуса плоскостью, не проходящей через его вершину (см. рис.33).

В полярной системе координат эти линии объединяет (кроме общего названия) еще и то, что они описываются одним и тем же уравнением, которое имеет вид

. (2.27)

У равнению (2.27) соответствует эллипс, если <1 , парабола при =1 и гипербола, при >1. Параметр p в (2.27) - параметр параболы, а для эллипса и гиперболы . При этом полюс полярной системы координат совмещается соответственно с левым фокусом эллипса, с правым

Рис. 33

фокусом гиперболы и с фокусом параболы. Соответствующие кривые приводятся на рис. 34 – 36.

Рис. 34

Рис. 35

Рис. 36

Поверхности второго порядка

Поверхности второго порядка - поверхности, описываемые уравнениями второго порядка (второй степени) относительно текущих координат.

Сфера - геометрическое место точек, равноудаленных от фиксированной точки С – центра сферы.

Уравнение сферы, построенное по приведенному определению:

(2.39)

Здесь R – радиус сферы, - центр сферы. Если центр сферы совпадет с началом координат, то a=b=c=0 и уравнение сферы будет:

Эллипсоид (рис. 42) - поверхность, описываемая уравнением

(2.40)

Если, a, b, c не равны между собой, то эллипсоид (2.40) называется трехосным эллипсоидом. В сечениях такого эллипсоида имеем эллипсы. Если какие-то две полуоси равны, например, , то эллипсоид

,

называется эллипсоидом вращения, поскольку он получается от вращения эллипса , на плоскости XOZ вокруг оси OZ . Если , то имеем сферу радиуса R=a с центром в начале координат.

Рис. 42

Однополостный гиперболоид-поверхность, описываемая уравнением

В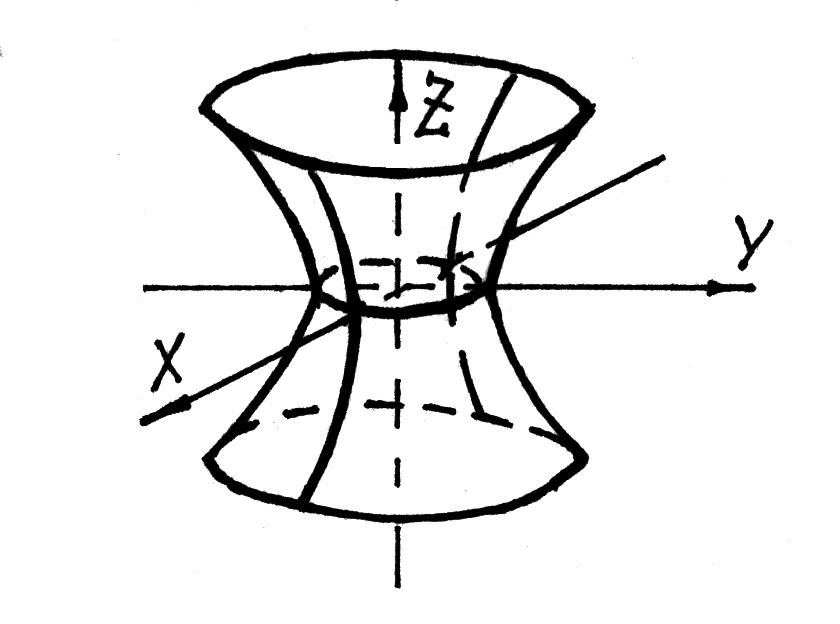 сечениях этой поверхности вертикальными координатными плоскостями XOZ и YOZ имеем гиперболы, а в сечениях горизонтальными плоскостя-

Рис. 43

ми XOY – эллипсы. Однополостный гиперболоид приводится на рис. 43.

Д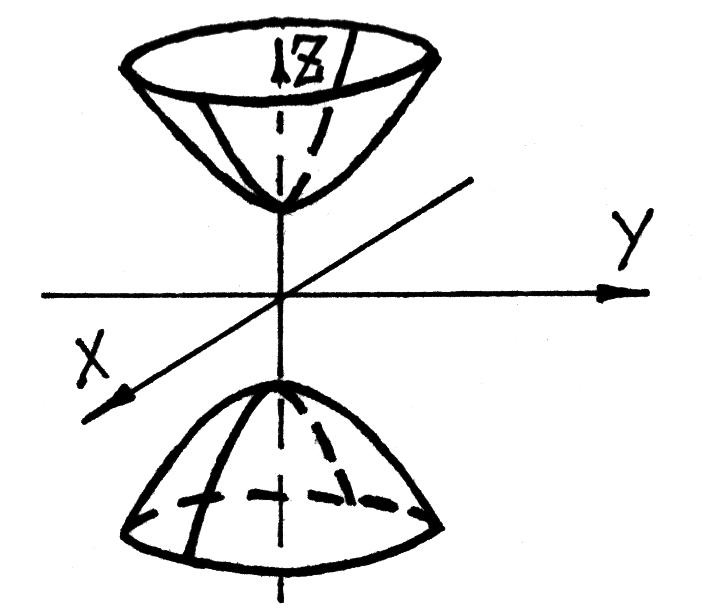 вуполостный гиперболоид – поверхность, описываемая уравнением

Рис. 44

В сечениях этой поверхности вертикальными координатными плоскостями

имеем гиперболы, а в сечениях горизонтальными плоскостями , где

– эллипсы. Двуполостный гиперболоид приводится на рис. 44.

Эллиптическому параболоиду соответствует уравнение

,

г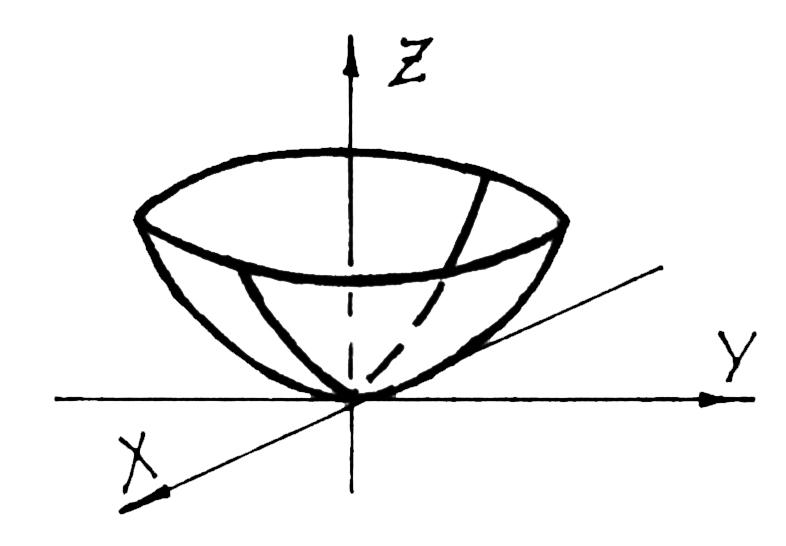 де a>0 и b>0 . В сечении этой поверхности вертикальными координатными плоскостями имеем параболы, а в сечениях горизонтальными плоскостями z=h, где h>0 - эллипсы. Поверхность приводится на рис. 45.

Рис. 45

Гиперболическому параболоиду соответствует уравнение

(a>0, b>0).

П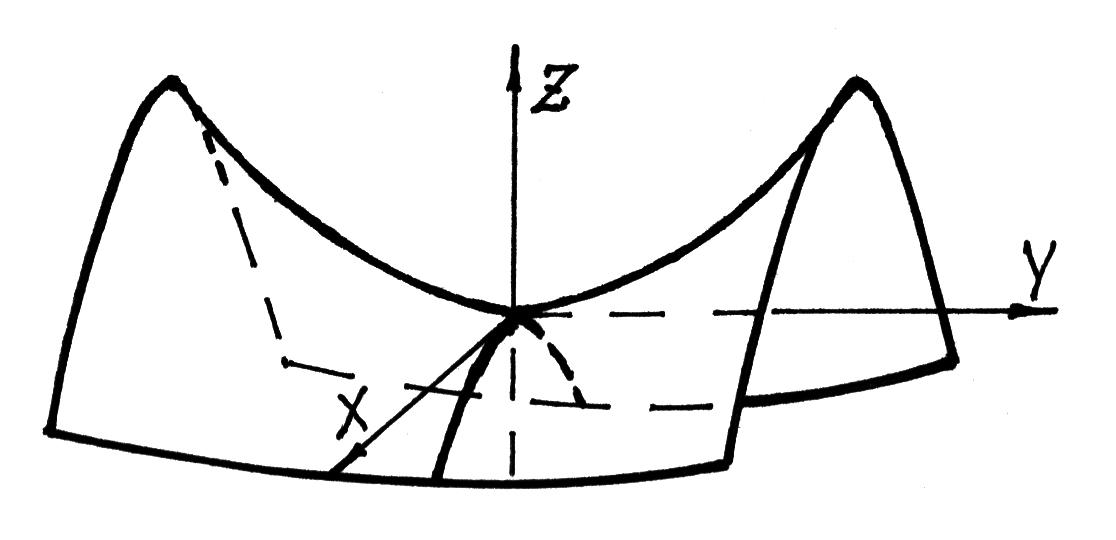 оверхность имеет вид изображенный на рис. 46. Как видим, поверхность имеет седлообразную форму. В сечениях вертикальными координатными

Рис. 46

плоскостями имеем параболы. В сечениях параллельных горизонтальной координатной плоскости, имеем гиперболы.

Цилиндром называется поверхность, образованная движением прямой линии (образующей), которая в процессе движения сохраняет свое направление и все время пересекает одну и ту же линию L - направляющую.

Наиболее простой вид имеют уравнения цилиндрических поверхностей, образующие которых параллельны одной из координатных осей. Пусть направляющей цилиндрической поверхности на плоскости XOY

является линия L (Рис. 47) , уравнение которой

F(x,y)=0, (2.41)

и пусть образующая рассматриваемой цилиндрической поверхности параллельна оси OZ. M(x,y,z) - произвольная точка цилиндрической поверхности. Точка M₁(x,y,0) - проекция этой точки на плоскость XOY. Посколь-

ку M L , то ее координаты удовлетворяют уравнению (2.41). А, т.к., точка M имеет те же абсциссу и ординату, что и точка M₁ , то ее коорди-

наты удовлетворяют уравнению (2.41) (координата z в уравнение

Рис.47

(2.41) не входит) и, следовательно, уравнение (2.41) есть уравнение рассматриваемой цилиндрической поверхности. Направляющая же - L описывается системой уравнений

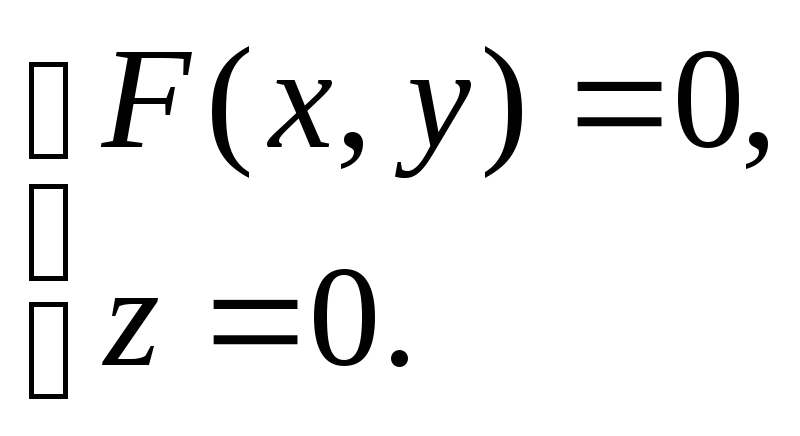
Таким образом, если в пространственной системе координат задается уравнение, в котором отсутствует одна из координат, то этому уравнению соответствует цилиндрическая поверхность. Образующая этой цилиндрической поверхности параллельна оси, координата которой отсутствует в рассматриваемом уравнении.

Конусом называется поверхность, описываемая при движении прямой линии (образующей), одна точка которой закреплена (вершина конуса); при этом движущаяся прямая все время пересекает некоторую линию (направляющую) (Рис. 48) .

П ростейшее уравнение конуса имеет вид:

(2.42)

Рис. 48

В сечениях (2.42) вертикальными координатными плоскостями имеем

пары пересекающихся прямых линий. В сечении горизонтальными плоскостями z=h - эллипсы.