
- •Аналитическая геометрия
- •Преобразование координат
- •Полярная система координат
- •2.1. Простейшие задачи аналитической геометрии
- •Аналитическая геометрия на плоскости
- •Прямая линия
- •Некоторые задачи на прямую
- •Аналитическая геометрия в пространстве Понятие об уравнениях поверхностей и линий в пространстве
- •Уравнения плоскости
- •Уравнения прямой в пространстве
- •Задачи на плоскость и прямую
Аналитическая геометрия
Геометрия – предмет, изучающий пространственные формы реального мира.
Аналитическая геометрия - предмет, изучающий геометрические образы при помощи алгебры.
В аналитической геометрии, с одной стороны, удается использовать аппарат алгебры в задачах геометрии, с другой стороны, решения многих задач алгебры получают наглядную геометрическую интерпретацию. Таким образом, достигается синтез двух важнейших отраслей математики, наблюдается их взаимопроникновение. В основе аналитической геометрии лежит метод координат, позволяющий определять точку пространства несколькими числами (координатами), а геометрические образы (линии, поверхности) – уравнениями, что дает возможность:
- описывать свойства фигур с помощью соотношений, связывающих координаты точек этих фигур;
- изучать (исследовать) эти соотношения средствами алгебры и анализа;
- делать выводы о геометрических свойствах фигур на основе исследования описывающих их соотношений.
Преобразование координат
Ниже
потребуется переходить от одной плоской
прямоугольной системы координат к
другой плоской прямоугольной системе
координат. Рассмотрим преобразование
координат, происходящее при таком
переходе. Пусть XOY
исходная прямоугольная система
координат иx, y
– координаты произвольной точкиMв этой системе. И пусть![]() -
новая система координат, начало
координат, которойO’
смещено относительно соответствующих
осей исходной системы в точкуC
cкоординатами(a,b)и координатные оси повернуты
относительно соответствующих осей
исходной системы на угол.
При этом координаты все той же точкиM в новой системе
обозначим черезx’
иy’ (рис. 27).
-
новая система координат, начало
координат, которойO’
смещено относительно соответствующих
осей исходной системы в точкуC
cкоординатами(a,b)и координатные оси повернуты
относительно соответствующих осей
исходной системы на угол.
При этом координаты все той же точкиM в новой системе
обозначим черезx’
иy’ (рис. 27).
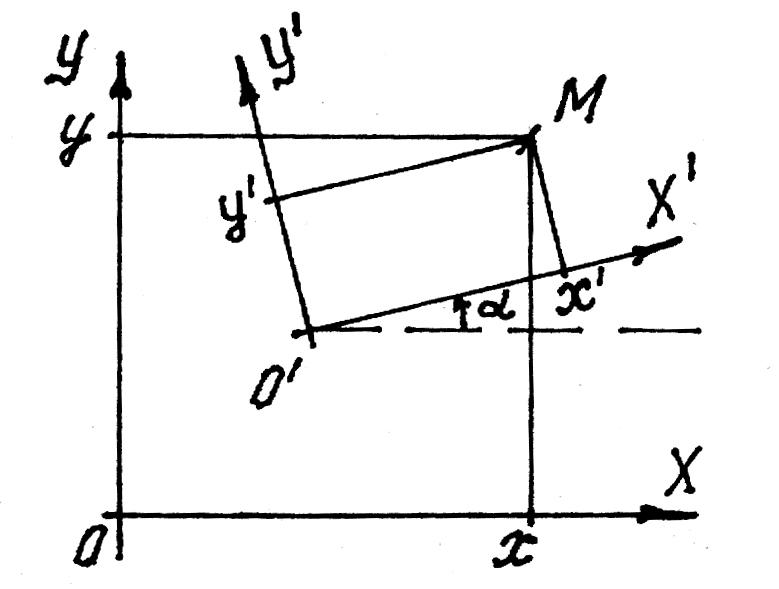 Рис.
27
Рис.
27
Координаты
x иy
исходной системы координат выражаются
через координаты
![]() и
и
![]() новой системы по формулам
новой системы по формулам
![]() (2.21)
(2.21)
а координаты новой системы через координаты исходной системы
![]() (2.22)
(2.22)
Уравнение смещенной параболы имеет вид
![]() ,
(2.23)
,
(2.23)
ч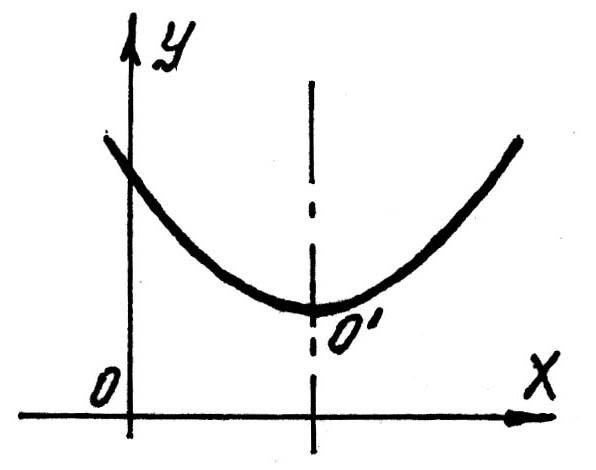 то
показывается с использованием
преобразований координат (2.21)-(2.22).
Парабола, соответствующая уравнению
(2.23), приведена на рис. 28.
то
показывается с использованием
преобразований координат (2.21)-(2.22).
Парабола, соответствующая уравнению
(2.23), приведена на рис. 28.
Рис. 28
Уравнению (2.23)
соответствует парабола, ось симметрии
которой параллельна оси ординат. Вершина
этой параболы
![]() имеет координаты
имеет координаты
![]() и
и
![]() .
Ветви параболы обращены вверх или вниз
в зависимости от того, положительно
числоAили отрицательно.
.
Ветви параболы обращены вверх или вниз
в зависимости от того, положительно
числоAили отрицательно.
Равносторонняя гипербола, асимптотами которой являются оси координат, имеет уравнение
![]() (2.24)
(2.24)
или
![]() ,
что так же показывается с использованием
формул (2.21) -(2.22). Гиперболы, соответствующие
уравнению (2.24), приводятся на рис. 29.
,
что так же показывается с использованием
формул (2.21) -(2.22). Гиперболы, соответствующие
уравнению (2.24), приводятся на рис. 29.
 Рис.
29
Рис.
29
Сплошной линией
приведена гипербола (2.24), когда
![]() ,
штриховой, когда
,
штриховой, когда![]() .
.
Полярная система координат
Полярная система координат определяетсяполюсом O иполярной осью OX на которой указывается масштабная единица (рис. 30).
П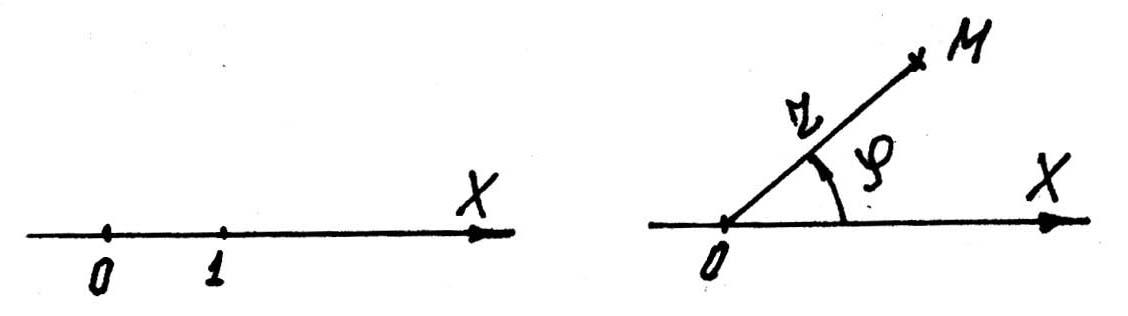 оложение
точки в полярной системе координат
определяетсяполярным радиусом r
– расстоянием от полюса до рассматриваемой
точки, иполярным углом ,
отсчитываемым от полярной оси до
соответствующего полярного радиуса
против хода часовой стрелки (рис. 31),
оложение
точки в полярной системе координат
определяетсяполярным радиусом r
– расстоянием от полюса до рассматриваемой
точки, иполярным углом ,
отсчитываемым от полярной оси до
соответствующего полярного радиуса
против хода часовой стрелки (рис. 31),![]()
Рис. 30 Рис. 31
С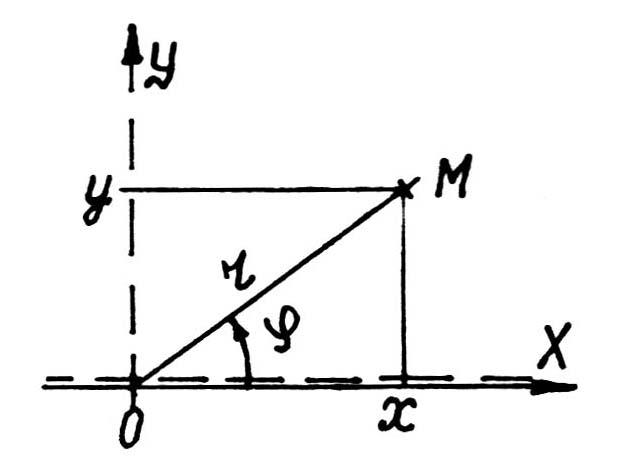 овмещая,
прямоугольную систему координат с
полярной так, что ось абсцисс прямоугольной
системы координат совпадает с полярной
осью, а ось ординат, проходящей через
полюс полярной системы ( рис. 32 ), полу-
овмещая,
прямоугольную систему координат с
полярной так, что ось абсцисс прямоугольной
системы координат совпадает с полярной
осью, а ось ординат, проходящей через
полюс полярной системы ( рис. 32 ), полу-
Рис. 32
чим соотношения, связывающие полярные координаты с прямоугольными.
Так формулы
![]()
![]() (2.25)
(2.25)
выражают прямоугольные координаты точки M через ее полярные координаты. Полярные координаты точки через ее прямоугольные координаты могут быть установлены по формулам
![]()
![]()
![]() .
(2.26)
.
(2.26)
