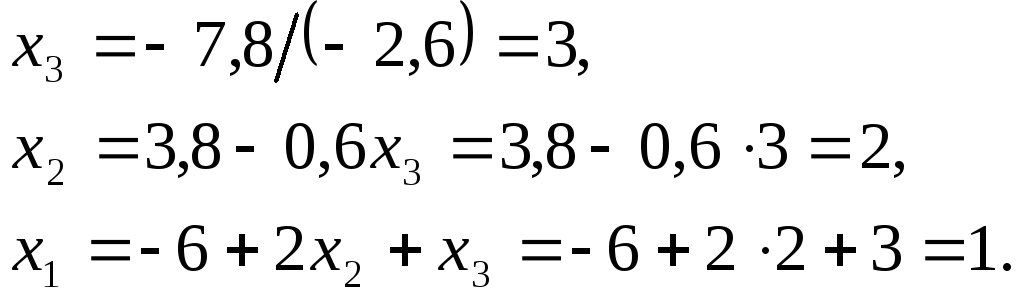5. Условие совместности системы линейных уравнений.

Система линейных уравнений снеизвестными имеет вид

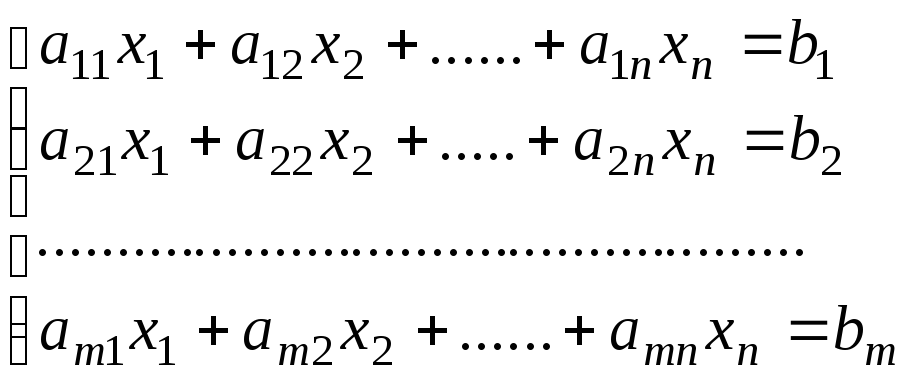. (5.1)

Система (5.1) называется однородной, если все ее свободные члены равны нулю и неоднородной в противном случае. Матрица из коэффициентов при неизвестных

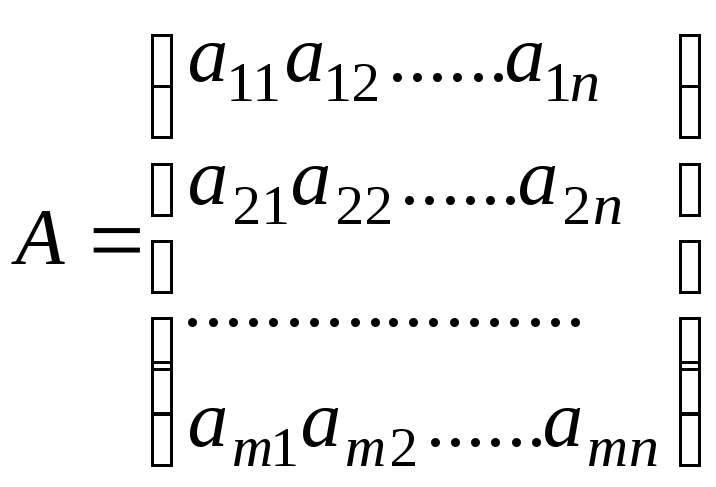(5.2)

называется матрицей системы (5.1), столбец

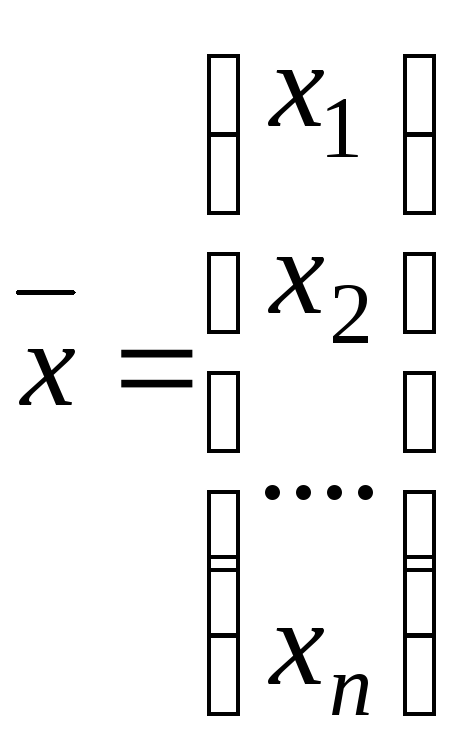(5.3)

- столбцом из неизвестных, а столбец

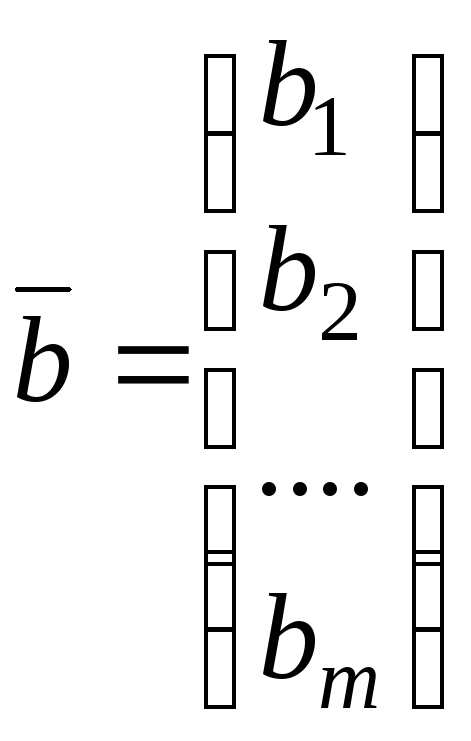(5.4)

- столбцом из свободных членов. Используя операцию умножения матриц и понятие равенства матриц, систему (5.1) можно переписать в виде

. (5.5)

Строка или столбец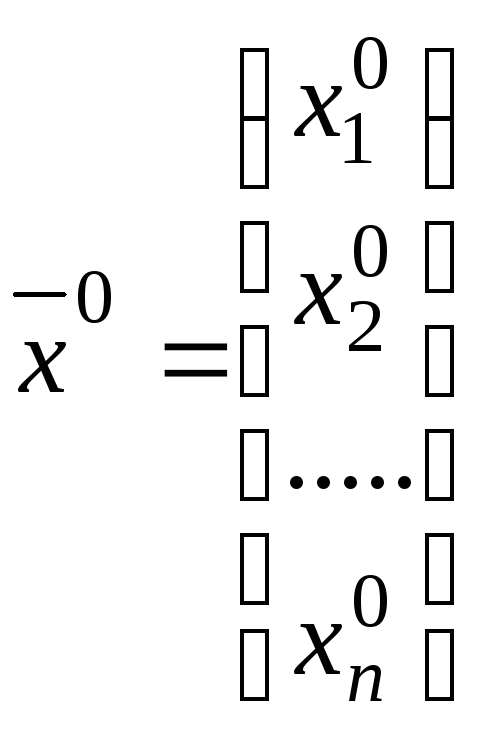называетсярешением системы (5.1), если каждое уравнение системы обращается в тождество после подстановки в него чисел вместо соответствующих неизвестных. Система (5.1) называетсясовместной, если она имеет хотя бы одно решение, и несовместной в противном случае. Две системы линейных уравнений называются эквивалентными или равносильными, если их решения равны или обе системы несовместны.

Припишем к матрице системы (5.2) столбец из свободных членов (5.4). Полученная матрица

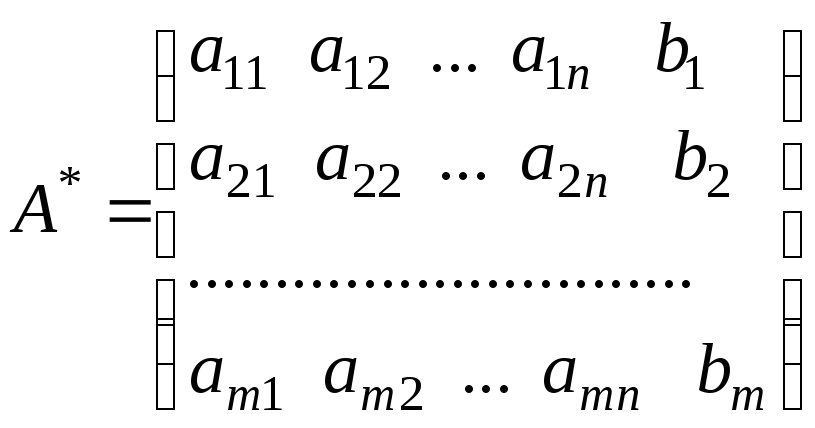
называется расширенной матрицей системы (5.1).

Теорема 5.1. (Кронекера-Капелли)

Для того чтобы система линейных уравнений (5.1) была совместна необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.

Доказательство. 1) Необходимость. Используя линейные операции со столбцами, перепишем систему (5.1) в виде

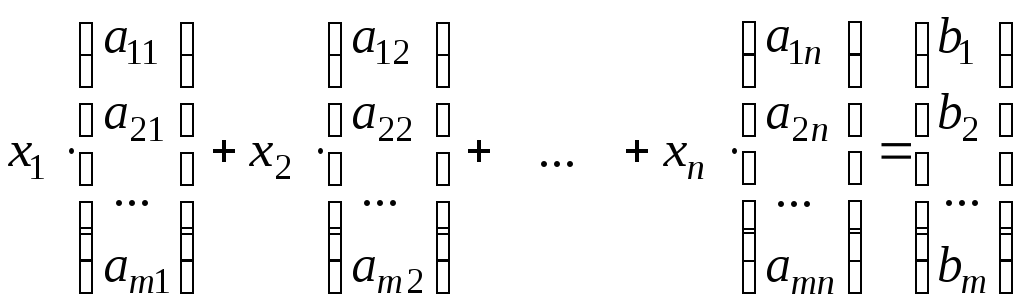. (5.6)

Пусть система (5.1) совместна, т.е. имеет хотя бы одно решение . При подстановке чиселв равенство (5.6) последнее обращается в тождество

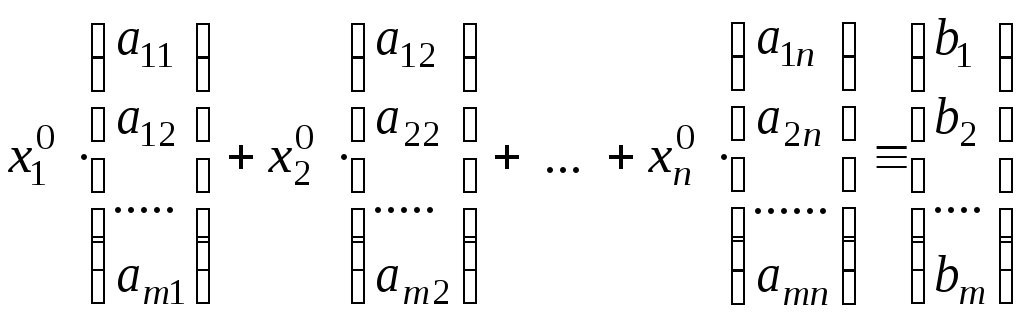. (5.7)

В силу (5.7) столбец из свободных членов есть линейная комбинация столбцов матрицы системы. Отсюда по предложению 1.1 все столбцы расширенной матрицы системы линейно зависимы. Значит, добавление столбца из свободных членов не увеличивает общего числа линейно независимых столбцов расширенной матрицы и по теореме о ранге матрицы .

2) Достаточность. Пусть . В этом случае базисный минор матрицыявляется базисным и в матрицеиначе по определению ранга. По теореме о базисном миноре столбец свободных членов есть линейная комбинация тех столбцов матрицы, в которых расположен базисный минор. Добавляя к этой линейной комбинации недостающие столбцы матрицыс нулевыми коэффициентами, получим представление (5.7) столбца свободных членов в виде линейной комбинации всех столбцов матрицы. Коэффициенты данной линейной комбинации составляют решение системы (5.1).

6. Правило Крамера.

Рассмотрим систему линейных уравнений снеизвестными

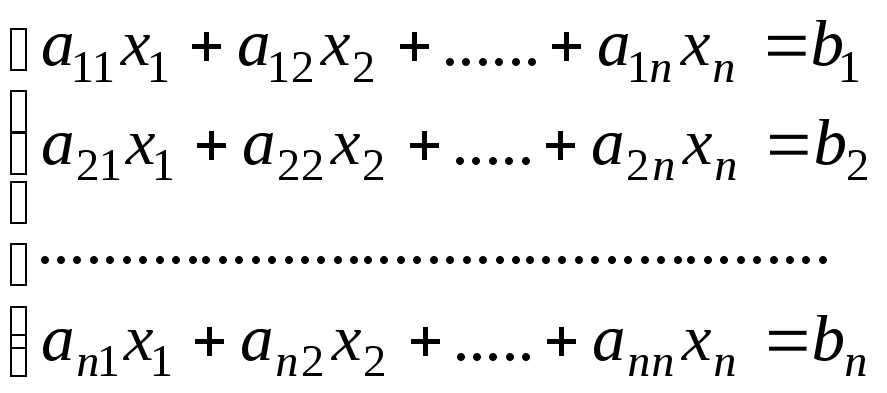. (6.1)

Теорема 6.1. (Правило Крамера)

Система (6.1) в случае, когда определитель матрицы системы (6.1) отличен от нуля, имеет решение и, причем только одно. Это решение находится либо по формуле

, (6.2)

где - обратная матрица к матрице системы (6.1), а- столбец свободных членов, либо по формулам

, (для всех ) (6.3)

где - определитель матрицы системы (6.1), а- определитель матрицы, полученной из матрицы системы заменойстолбца столбцом свободных членов.

Доказательство. Запишем систему (6.1) в виде (5.5)

. (6.3)

Так как , то по теореме 3.2 матрицаА имеет обратную . Покажем сначала, что столбец, определяемый формулой (6.2), есть решение уравнения (6.3). Подставим столбец (6.2) в уравнение (6.3). Получим

, или , или, или,

т.е. столбец (6.2) является решением уравнения (6.3). Существование решения уравнения (6.3) доказано, остается доказать его единственность.

Пусть - какое-либо решение уравнения (6.3). При подстановке этого решения в уравнение (6.3) последнее обращается в тождество

. (6.4)

Умножив тождество (6.4) слева на , получим

, или , или, или.

Таким образом, любое решение уравнения (6.3) совпадает с (6.2). Тем самым единственность решения уравнения (6.3) доказана.

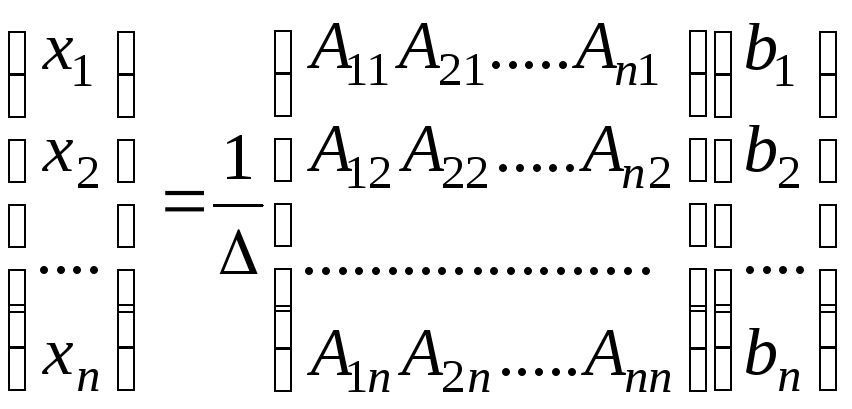
Преобразуем теперь решение (6.2) следующим образом. Заменив в (6.2) их выражениями (5.3), (3.3) и (5.4), получим

,

или после перемножения матриц

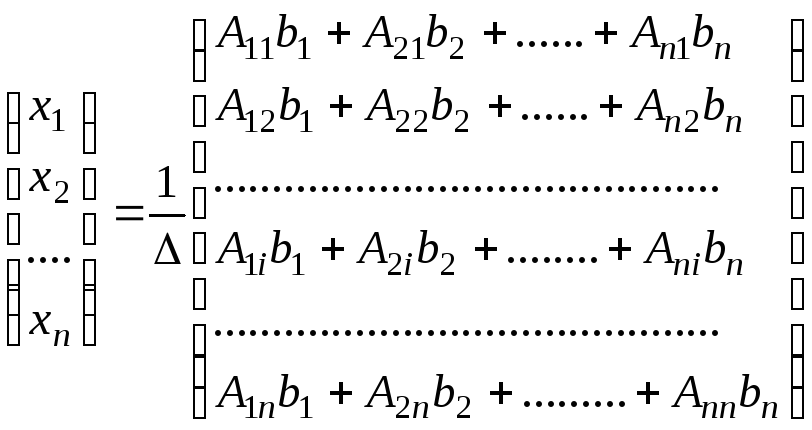. (6.5)

У матрицы в правой части (6.5) строка представляет собой разложение определителя

по столбцу, так как алгебраические дополнения элементовстолбца в матрице

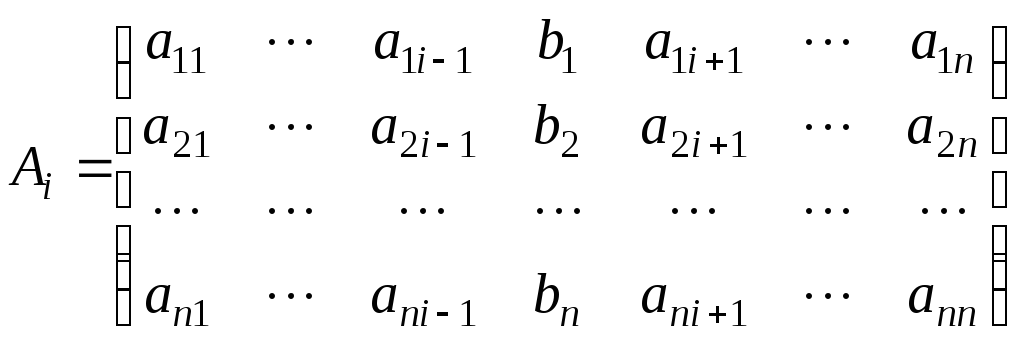
совпадают с . В силу этого равенства (6.5) можно записать

,

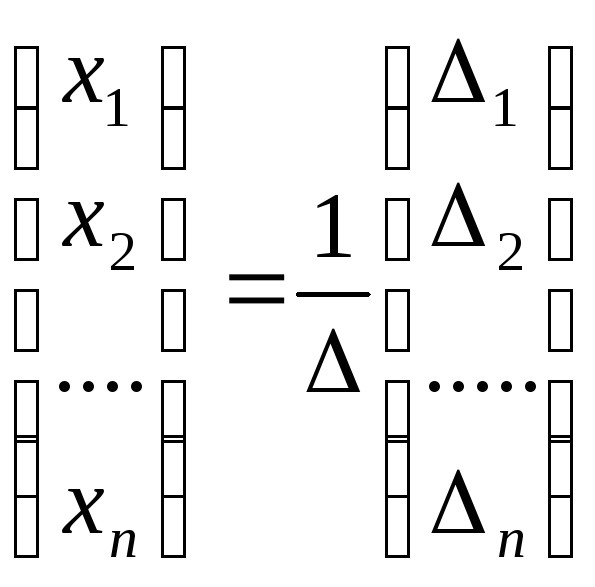или после умножения матрицы на число, в виде

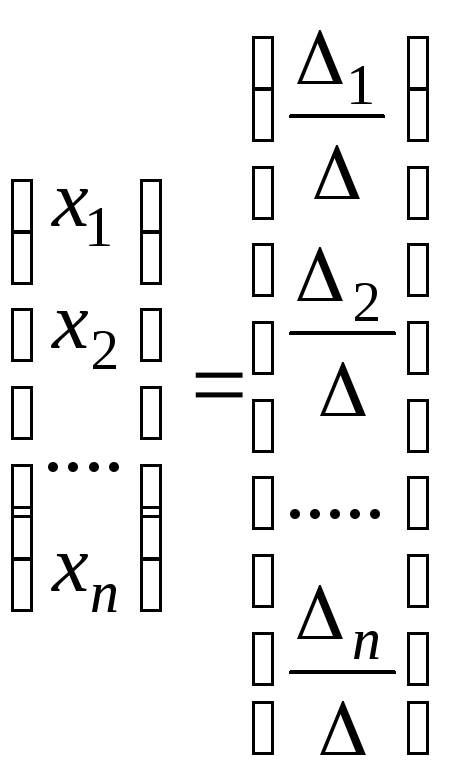. (6.6)

Приравнивая соответствующие элементы матриц в (6.6), получим формулы (6.3). Они носят название формул Крамера.

Матричный способ решения

Обозначим

, , ,

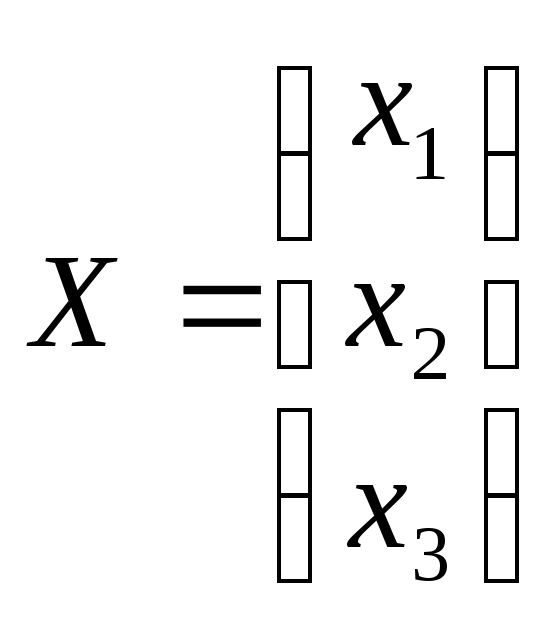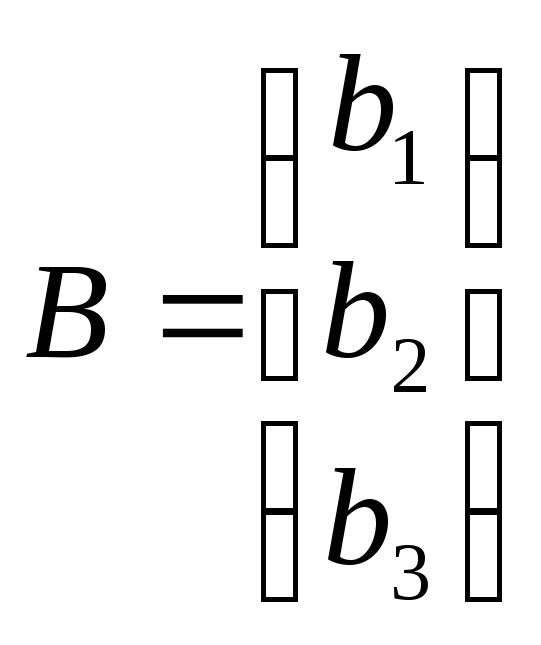где - матрица коэффициентов при неизвестных,- матрица-столбец неизвестных, - матрица свободных членов в системе (1.1). Тогда систему (1.1) в матричной форме можно записать в виде

, (6.7)

поскольку

.

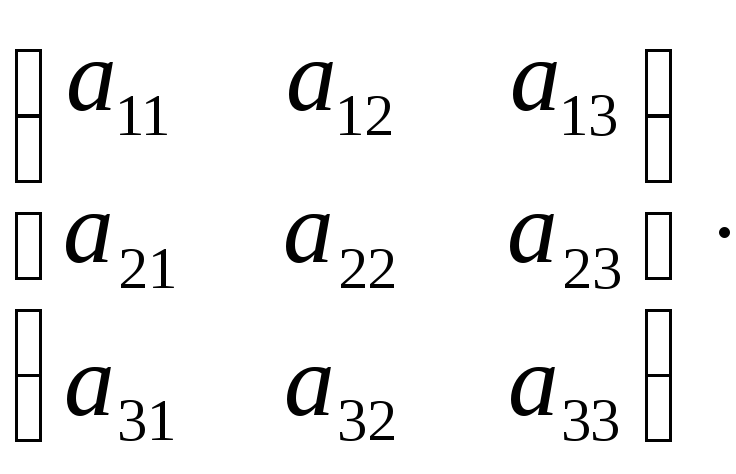
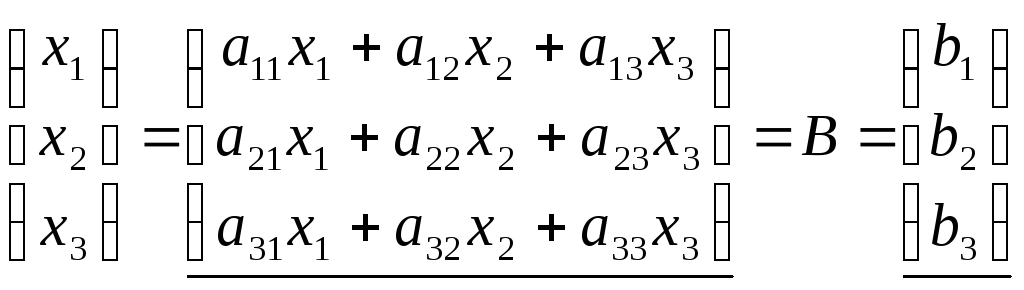Из равенства подчеркнутых матриц в цепи следует система (1.1).

Решение матричной системы (1.2) будет

.

Таким образом, матрица неизвестных равна произведению матрицы - матрице обратной по отношению к матрице коэффициентов на матрицу свободных членов .

П р и м е р . Решим матричным способом (с использованием обратной матрицы) систему ранее решенную методом Крамера :

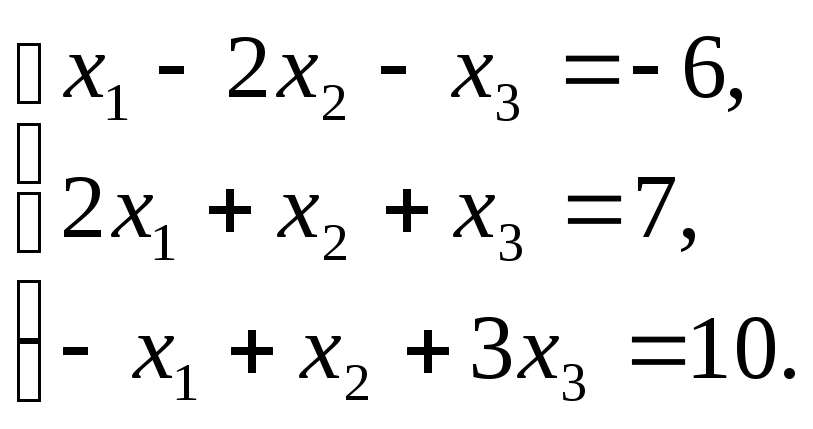
Р е ш е н и е . Для рассматриваемой системы

,,.

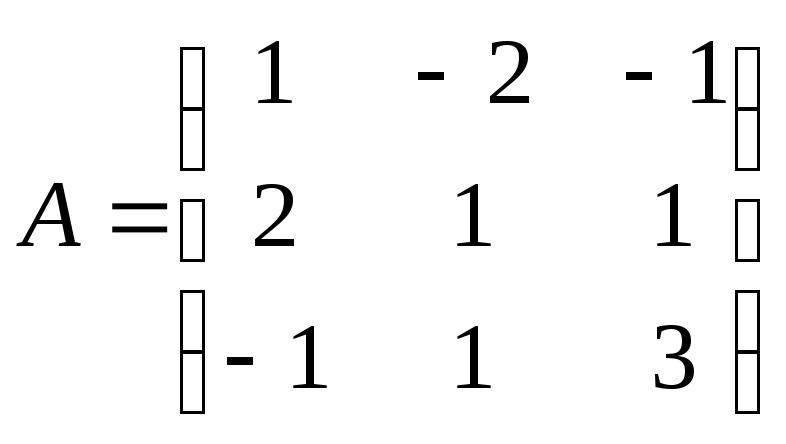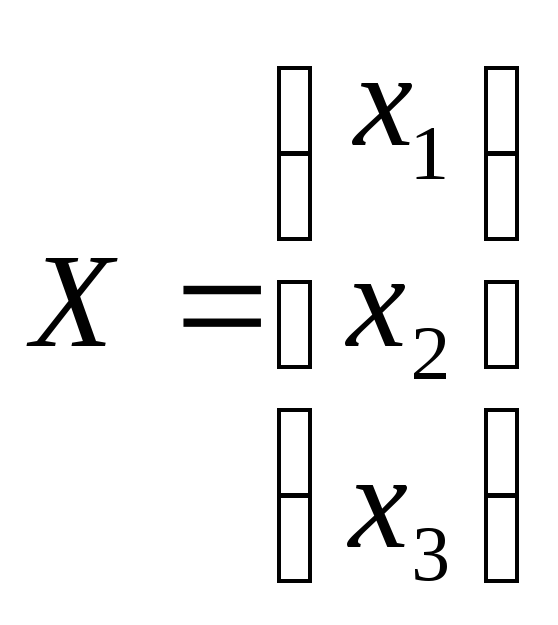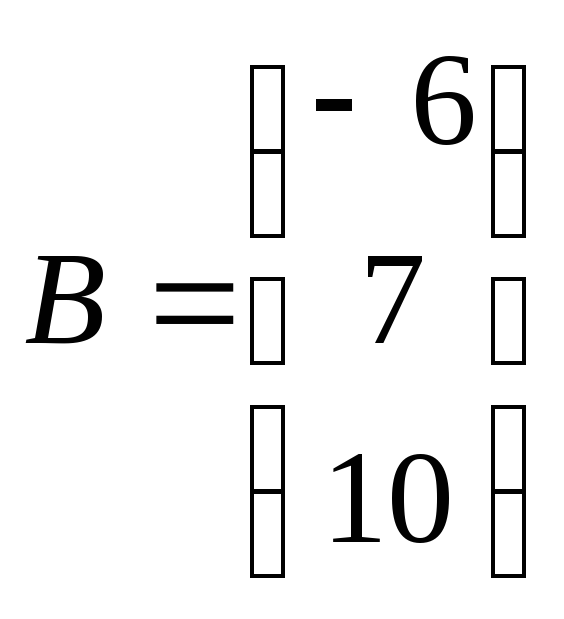Строим матрицу :

определитель , соответствующий матрице, будет

,

алгебраические дополнения элементов определителя , будут

,,,

,,,

,,;

матрица - матрица алгебраических дополнений определителя

;

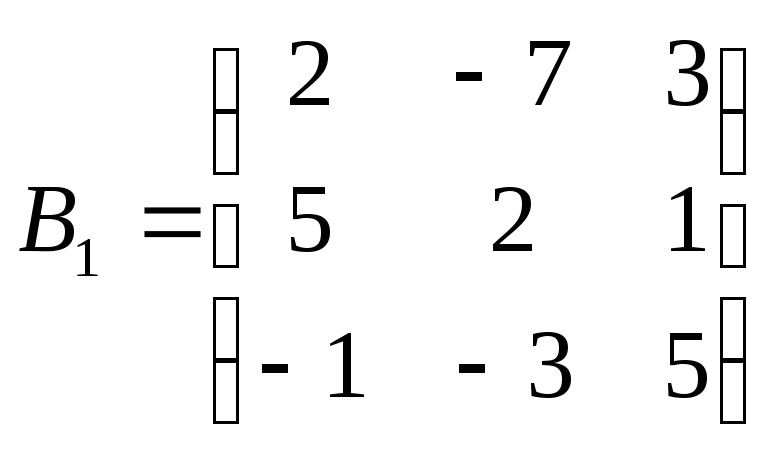матрица

.

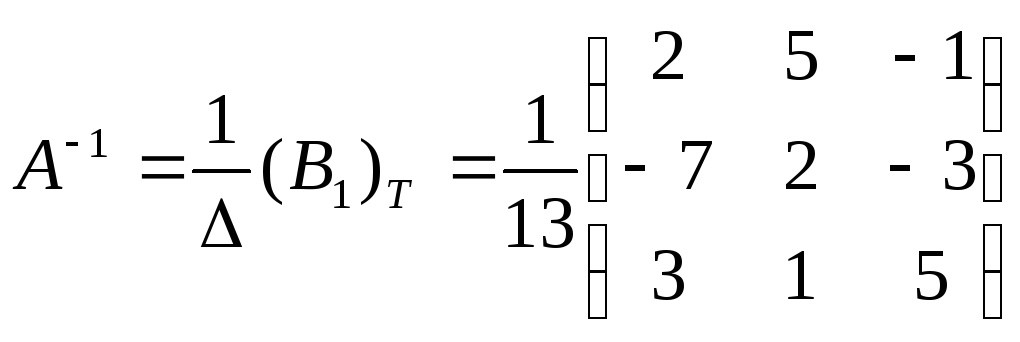П р о в е р к а

,

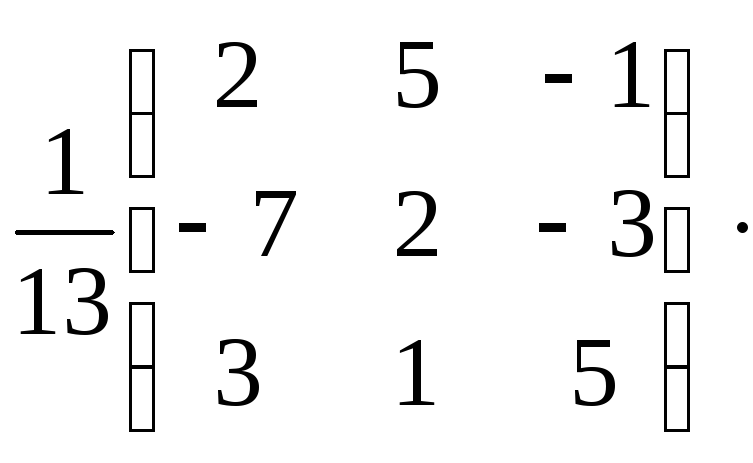
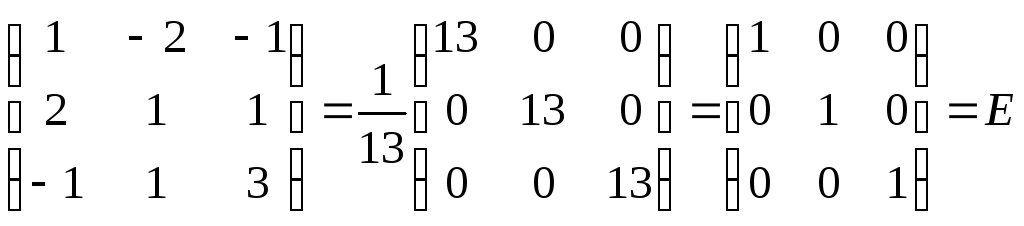обратная матрица найдена, верно.

Теперь

=,

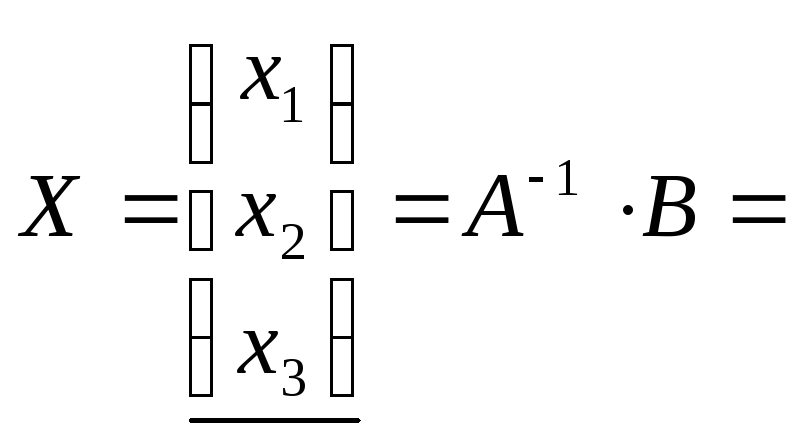
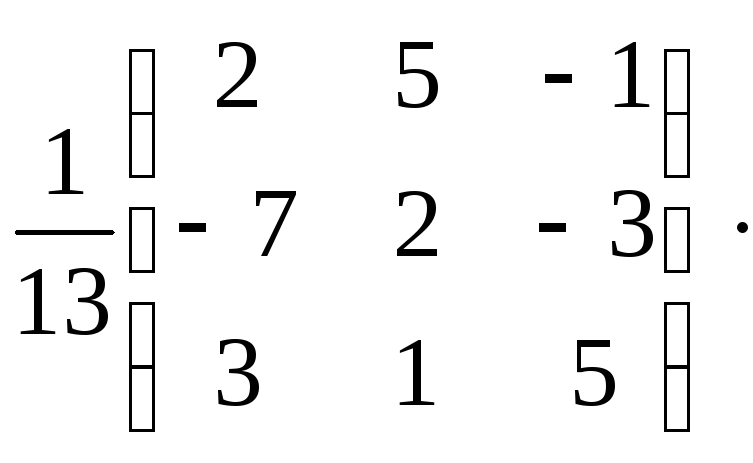
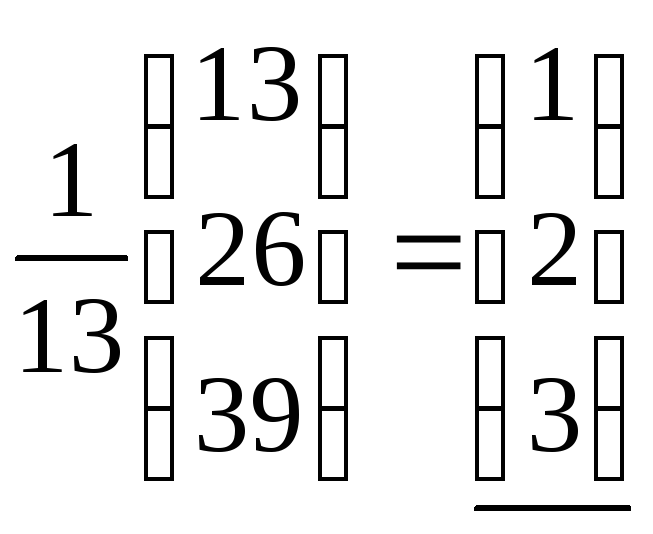из подчеркнутых частей цепи ,,.

Метод Гаусса исключения неизвестных

Две системы линейных алгебраических уравнений называются эквивалентными, если каждое решение первой системы является решением второй, и наоборот.

Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:

- перестановка двух уравнений;

-умножение обеих частей одного из уравнений на любое отличное от нуля число;

-прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на одно и то же число.

Элементарные преобразования переводят данную систему уравнений в эквивалентную ей систему.

Используя понятие элементарных преобразований, метод Гаусса позволяет свести систему n уравнений с n неизвестными к ступенчатой эквивалентной треугольной системе, когда первое уравнение содержит все n неизвестных, второе уравнение содержит (n-1) неизвестную, третье – (n-2) неизвестных, и т.д., последнее уравнение содержит одну неизвестную.

Удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу из коэффициентов при неизвестных и свободных членов. Рассмотрим метод Гаусса на примере ранее решенной двумя методами системы.

П р и м е р . Решить методом Гаусса систему:

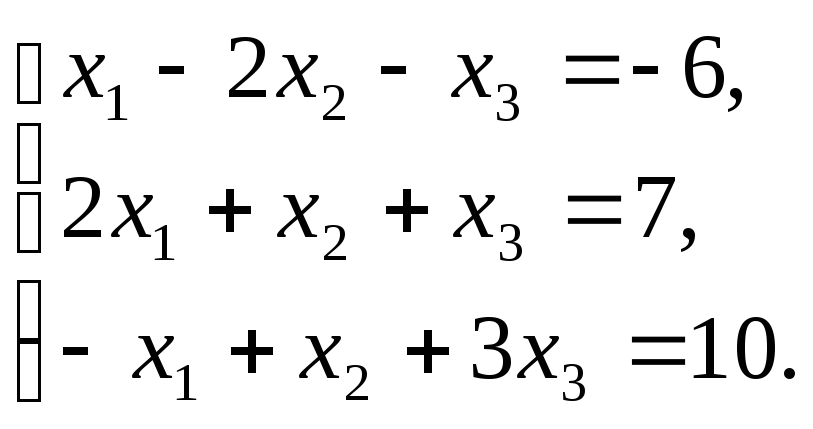
Р е ш е н и е .

Запишем расширенную матрицу (матрицу коэффициентов и свободных членов), соответствующую решаемой системе, и последовательно преобразуем ее

.

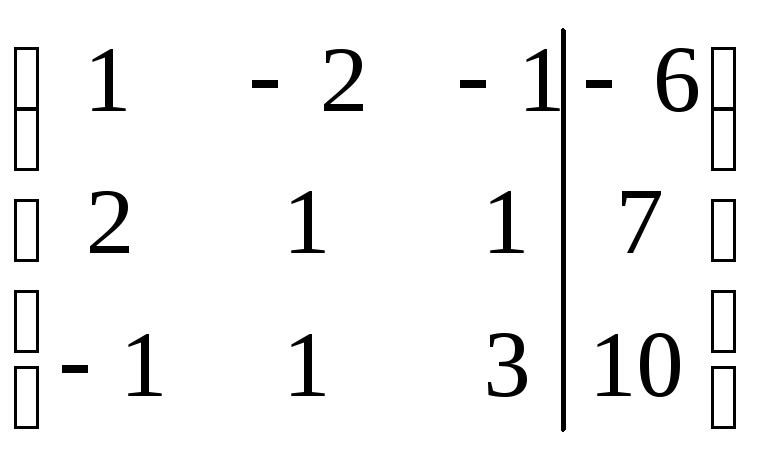
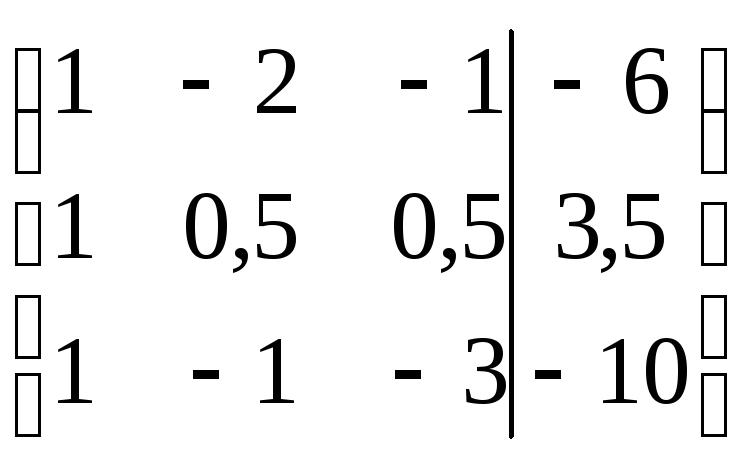
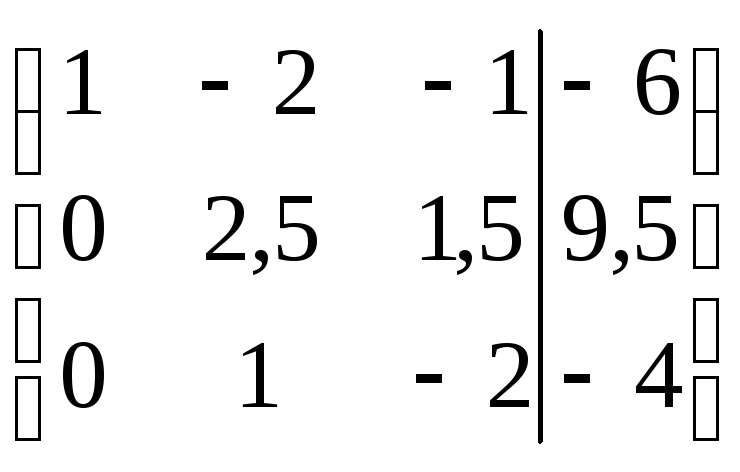
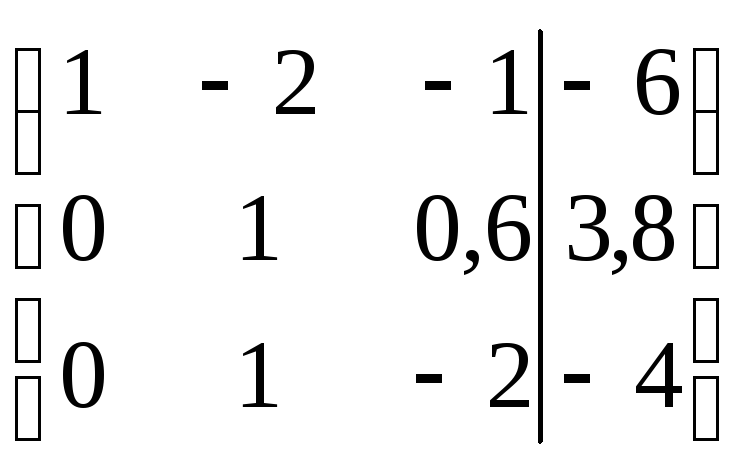
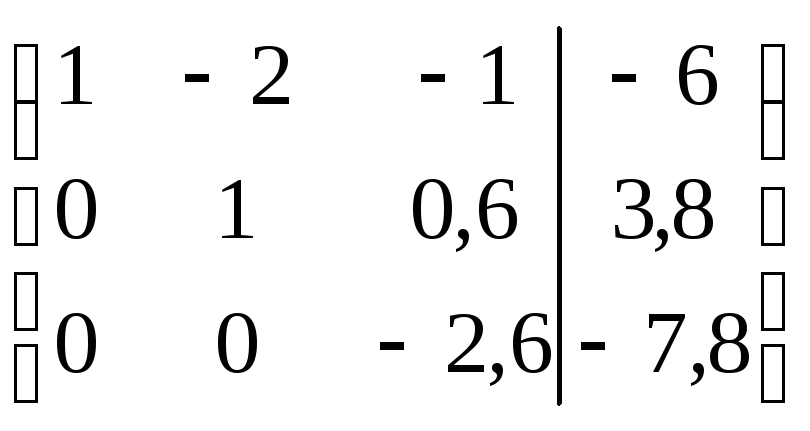Вторая матрица получена из первой расширенной матрицы системы путем деления каждого уравнения на их коэффициенты при неизвестной (члены первого уравнения делились на 1, второго – на 2, третьего – на -1). Третья матрица получена из второй путем вычитания из элементов второго и третьего уравнений соответствующих элементов первого уравнения. Четвертая матрица получена из третьей матрицы путем деления элементов второй строки (второго уравнения) на 2.5 и деления элементов третьей строки на 1. Пятая матрица получена из четвертой путем вычитания из элементов третьей строки соответствующих элементов второй строки. Пятой матрице соответствует следующая ступенчатая треугольная система

из которой, без затруднения, получаем решение