Два замечательных предела

Теорема 10.1.(первый замечательный предел).

Доказательство.В круге радиуса, равного единице, рассмотрим уголх, удовлетворяющий условию. Из рис. 10.1 имеем

. (10.1)

Но ,, откуда в силу (10.1)

. (10.2)

Рис. 10.1

Далее, из того же рисунка имеем

. (10.3)

Но . (10.4)

, откуда на основании (10.2)

. (10.5)

Таким образом, в силу (10.3), (10.4) и (10.5)

или

. (10.6)

Из (10.2) и (10.6) имеем или

. (10.7)

Рассмотрим теперь угол х, удовлетворяющий условию. Тогдаи на основании (10.7)или.

Итак, в проколотой окрестности точки три функции,,1связаны неравенством (10.7). При этом.

Тогда по теореме 8.2

.

Пример.Вычислить. Имеем.

Положим . Отсюда. По теореме 10.1. Итак,,, откуда в силу теоремы 7.5 о пределе сложной функциии.

Теорема 10.2.(второй замечательный предел).

Доказательство этой теоремы можно найти в [1],[2].

Указанные выше пределы часто встречаются в математике и поэтому носят названия «замечательных».

11.Непрерывность функции в точке

Определение 11.1.Функцияназывается непрерывной в точке , если предел этой функции в точкесуществует и равен значению, т.е.. Функциянепрерывна на множестве, если она непрерывна в каждой точке этого множества.

Назовем полным приращением функции в точкефункцию, определяемую формулой

, (11.1)

где - любая точка из области задания. Пусть. Обозначим,, …, и назовем их приращениями аргументов функциив точке.

Используя эти обозначения, получим для полного приращения , соответствующего приращениям аргументовследующее выражение:

.

Теорема 11.1.Для непрерывности функциив точкенеобходимо и достаточно, чтобы ее полное приращениебыло бесконечно малой величиной в точке.

Доказательство.Пусть функциянепрерывна в точке, т.е., или по свойству предела, или согласно (11.1), что и требовалось доказать.

Рассмотрим теперь основные свойства непрерывных функций в точке.

Теорема 11.2.Если функцииинепрерывны в точке, то в этой точке непрерывны их сумма, разность, произведение и частное (последнее при условии).

Доказательство.Рассмотрим случай частного (для остальных случаев рассуждения аналогичны). Пустьинепрерывны в точке, т.е.,и. Тогда по теореме 7.4

.

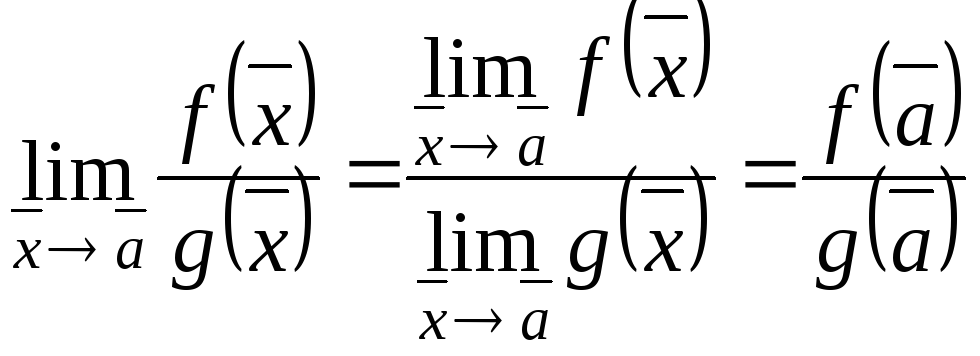Это значит, что непрерывна в точке.

Теорема 11.3.Если функциинепрерывны в точке, а функциянепрерывна в точке, где, то сложная функциянепрерывна в точке.

Доказательство. Пусть функции , гденепрерывны в точке, т.е., а функциягденепрерывна в точке, т.е.. Тогда по теореме 7.5, что означает непрерывность сложной функциив точке.

Теорема 11.4.Если функциянепрерывна в точкеито существует такая окрестность точки, в пределах которойимеет один и тот же знак, совпадающий с знаком.

Доказательство. Пустьнепрерывна в точке, т.е.и. Тогда по теореме 8.3 существует такая окрестность точки, в пределах которой.

Основными элементарными функцииодной переменной называются:

1) Степенная функция , где.

2) Показательная функция , где.

3) Логарифмическая функция , где.

1. Тригонометрические функции ,,,.

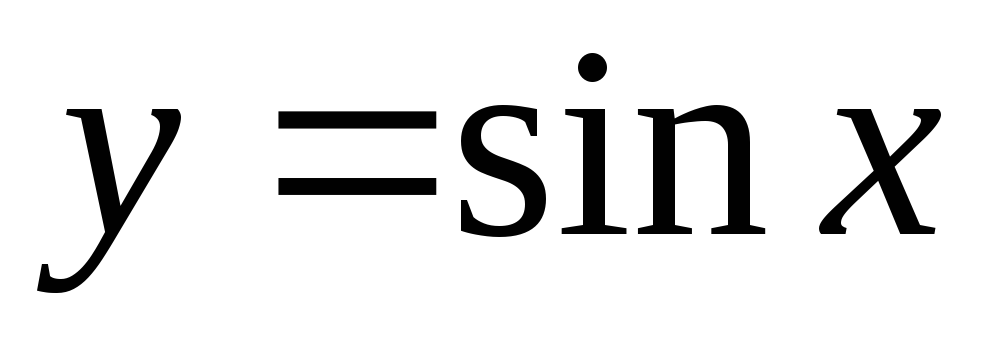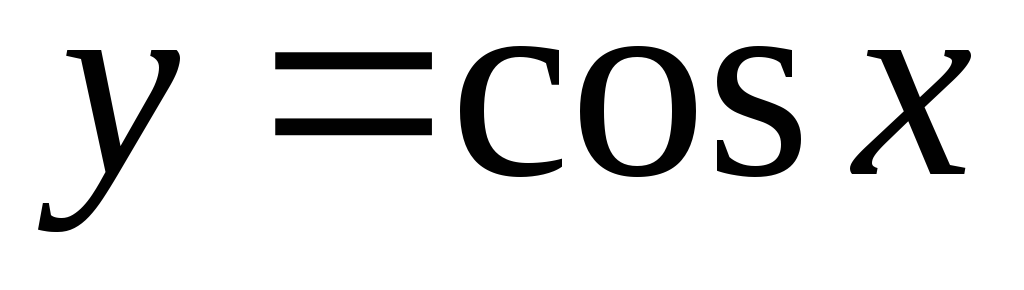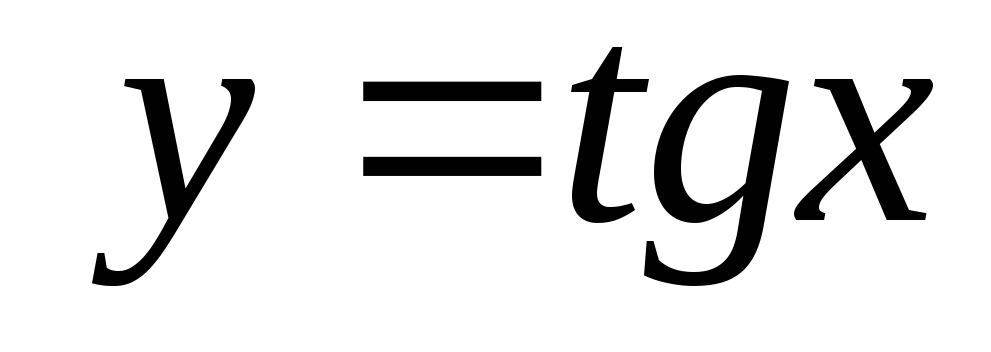2. Обратные тригонометрические функции ,,,.

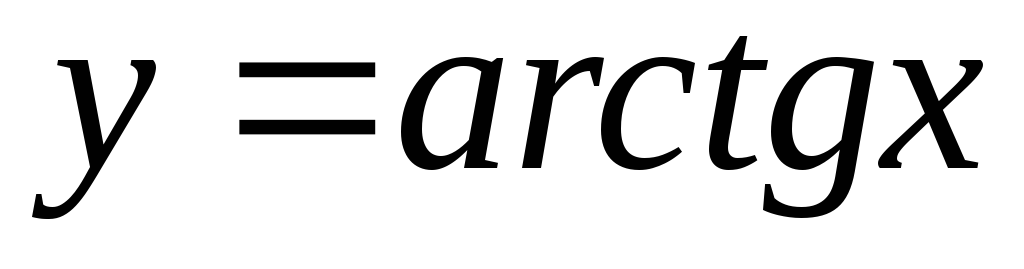Доказывается, что все основные элементарные функции непрерывны в каждой точке области задания.

Элементарной функциейназывается любая функция, получаемая из основных элементарных функций и констант посредством конечного числа арифметических действий и операции суперпозиции.

Теорема 11.5.Элементарные функции непрерывны в каждой точке области задания.

Утверждение теоремы вытекает из непрерывности основных элементарных функций в точках области задания и теорем 11.2 и 11.3.

Из теоремы 11.5. следует, что если элементарная функция определена в предельной точке, то предел этой функции равен ее значению в предельной точке.В противном случае нахождение предельного значения требует дополнительных исследований.