
Лекции. Математика / Сем1_лекция 1
.doc1. Обозначения. Матрицы.
n
– мерным вектором,
где n
– фиксированное натуральное число,
называется упорядоченная система
![]() из n
действительных чисел. Числа
из n
действительных чисел. Числа
![]() условимся называть координатами
вектора
условимся называть координатами
вектора
![]() .
Вектор
.
Вектор
![]() ,
все координаты которого равны нулю,
называется нулевым. Суммой
двух n-мерных векторов
,
все координаты которого равны нулю,
называется нулевым. Суммой
двух n-мерных векторов
![]() и
и
![]() называется вектор
называется вектор
![]() .
.
Произведение
вектора
![]() на действительное
число
на действительное
число
![]() определяется формулой
определяется формулой
![]() .
Скалярным
произведением двух n-мерных
векторов
.
Скалярным
произведением двух n-мерных
векторов
![]() и
и
![]() называется число
называется число
![]() ,
то есть сумма произведений соответствующих
координат векторов
,
то есть сумма произведений соответствующих
координат векторов
![]() и
и
![]() .
.
Линейной
комбинацией n
- мерных векторов
![]() с числовыми коэффициентами
с числовыми коэффициентами
![]() называется n-мерный
вектор
называется n-мерный
вектор
![]() .
Линейную комбинацию будем называть
тривиальной,
если все ее коэффициенты равны нулю.
.
Линейную комбинацию будем называть
тривиальной,
если все ее коэффициенты равны нулю.
Определение
1.1. Система
n-мерных
векторов
![]() называется линейно
зависимой,
если существует равная нулевому вектору
нетривиальная линейная комбинация этих
векторов, т.е. существуют неравные
одновременно нулю числа
называется линейно
зависимой,
если существует равная нулевому вектору
нетривиальная линейная комбинация этих
векторов, т.е. существуют неравные
одновременно нулю числа
![]() ,
такие что
,
такие что
![]() .
.
В
противном случае система n-мерных
векторов
![]() называется линейно
независимой,
т.е. векторы
называется линейно
независимой,
т.е. векторы
![]() линейно независимы, если любая линейная
комбинация этих векторов равна нулевому
вектору лишь при условии равенства нулю
всех ее числовых коэффициентов.
линейно независимы, если любая линейная
комбинация этих векторов равна нулевому
вектору лишь при условии равенства нулю
всех ее числовых коэффициентов.
Нетрудно проверяются следующие предложения:
Предложение 1.1. Система векторов линейно зависима тогда и только тогда, когда хотя бы один из них есть линейная комбинация остальных.
Предложение 1.2. Система, содержащая нулевой вектор, линейно зависима.
Предложение 1.3. Если некоторые из векторов системы сами по себе образуют линейно зависимую подсистему, то вся система линейно зависима.
Предложение 1.4. Любая подсистема линейно независимой системы векторов сама линейно независима.
Определение 1.2. Числовой матрицей размера m×n, где m и n - фиксированные натуральные числа, называется таблица
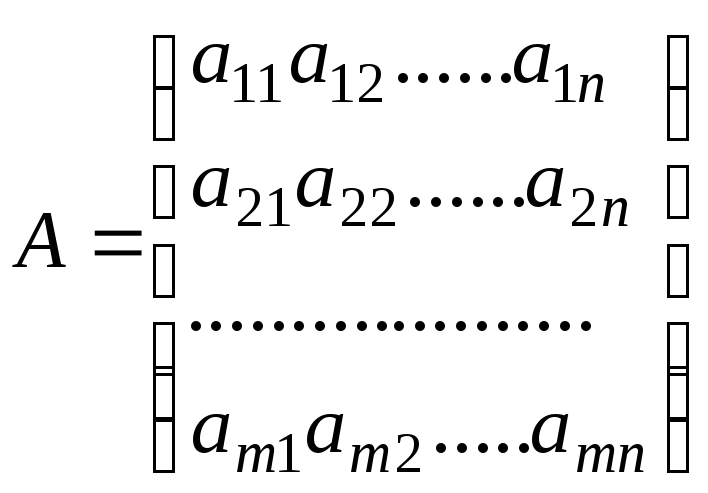 (1.1)
(1.1)
из
![]() чисел,
расположенных в виде таблицы из m
строк и n
столбцов.
чисел,
расположенных в виде таблицы из m
строк и n
столбцов.
Числа,
составляющие матрицу, называются ее
элементами. Их удобно обозначать одной
буквой с двумя индексами, первый из
которых обозначает номер строки, а
второй – номер столбца, на пересечении
которых расположен данный элемент.
Строки матрицы А
являются n–мерными
векторами, а столбцы - m–мерными
векторами. В свою очередь, каждый
записанный в строку n
– мерный вектор
![]() можно рассматривать как матрицу размера
1×n,
а каждый, записанный в столбец, m-мерный
вектор
можно рассматривать как матрицу размера
1×n,
а каждый, записанный в столбец, m-мерный
вектор
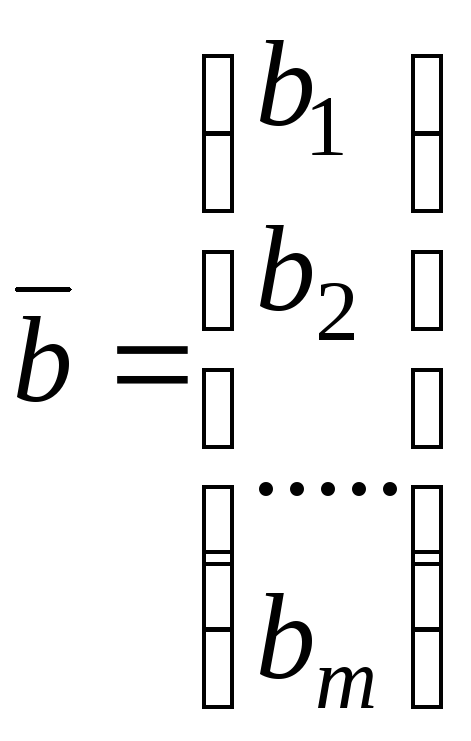 - как матрицу размера m×1.
- как матрицу размера m×1.
Матрица,
все строки или столбцы которой есть
нулевые векторы, называется нулевой
и обозначается 0. Матрица размера n×n
называется
квадратной
матрицей n-го
порядка.
Систему элементов
![]() квадратной матрицы будем называть ее
главной
диагональю,
а систему элементов
квадратной матрицы будем называть ее
главной
диагональю,
а систему элементов
![]() - ее побочной
диагональю.
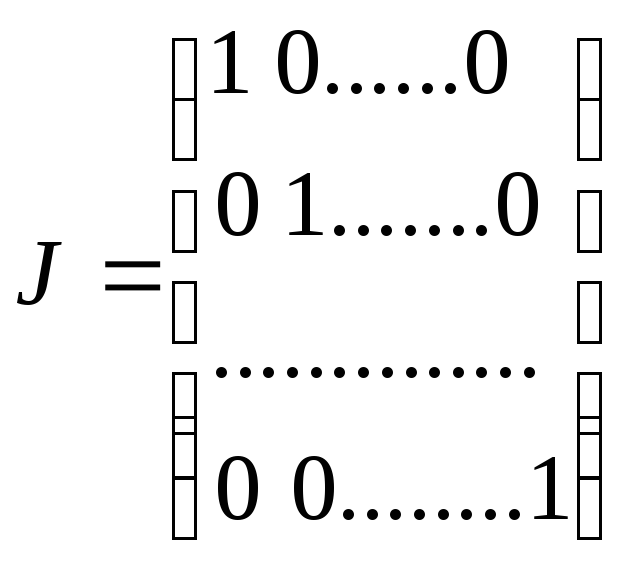
Квадратная матрица вида
- ее побочной
диагональю.
Квадратная матрица вида
 ,
,
где на главной диагонали стоят единицы, а на остальных местах нули, называется единичной матрицей. Две матрицы одинакового размера называются равными, если их соответствующие элементы равны.
Суммой
двух матриц А
и В
одного и того же размера
называется матрица А+В,
строки (столбцы) которой равны суммам
соответствующих строк (столбцов) матриц
А
и В.
Произведением матрицы А
на число
![]() называется матрица
называется матрица
![]() ,
строки (столбцы) которой равны произведениям
строк (столбцов) матрицы А
на число
,
строки (столбцы) которой равны произведениям
строк (столбцов) матрицы А
на число
![]() .
Из определения операций сложения матриц
и умножения матрицы на число, а также
из свойств чисел непосредственно
вытекают следующие свойства этих
операций:
.
Из определения операций сложения матриц
и умножения матрицы на число, а также
из свойств чисел непосредственно
вытекают следующие свойства этих
операций:
А+В=В+А, 1А=А,
(А+В)+С=А+(В+С, α(βA)=(αβ)А, (1.2)
А+0=А, (α+β)А=αA+βA,
А+(-1)А=0, α(A+B)=αA+αB.
Пусть
даны матрицы А
размера m×n
со строками
![]() и матрица В
размера n×p
с столбцами
и матрица В
размера n×p
с столбцами
![]() .
Произведением
матриц А
и В
называется матрица АВ
размера m×p,
элемент которой на пересечении
.
Произведением
матриц А
и В
называется матрица АВ
размера m×p,
элемент которой на пересечении
![]() строки и
строки и
![]() столбца,
где
столбца,
где
![]() равен скалярному произведению
равен скалярному произведению
![]() n-мерных
векторов
n-мерных
векторов
![]() и
и
![]() .
.
Умножение матриц ассоциативно, т.е. (АВ)С=А(ВС) и дистрибутивно относительно сложения, т.е. А(В+С)=АВ+АС. Однако умножение матриц не обладает свойством коммутативности, т.е. не всегда АВ=ВА. Например,
![]() ,
а
,
а
![]() .
.
Матрицы А и В, удовлетворяющие условию АВ=ВА, называются перестановочными. Например, единичная матрица J перестановочна с любой квадратной матрицей А того же порядка, причем
![]() .
(1.3)
.
(1.3)
Сопоставим
матрице (1.1) матрицу
![]() размера
размера
![]() ,
строки которой, совпадают с соответствующими
столбцами А
(и следовательно столбцы с соответствующими
строками матрицы А).
Матрица
,
строки которой, совпадают с соответствующими
столбцами А
(и следовательно столбцы с соответствующими
строками матрицы А).
Матрица
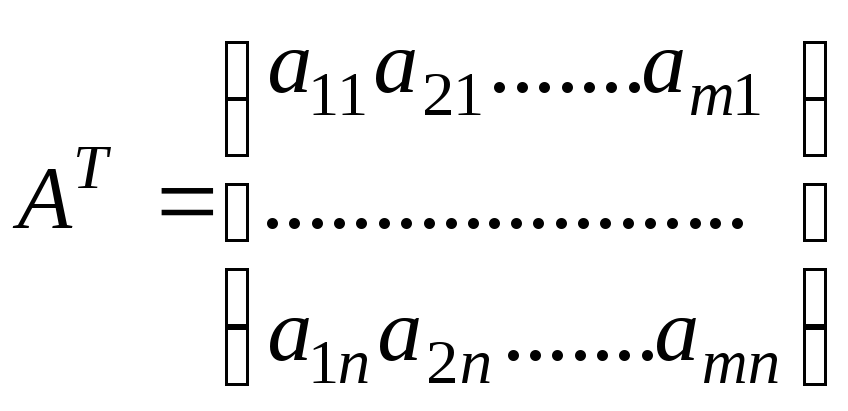
называется транспонированной матрицей А, а переход от А к АТ – транспонированием.
2. Определители.
С каждой квадратной матрицей связывается некоторое число, называемое определителем или детерминантом данной матрицы. Это число вычисляется по элементам матрицы определенным образом. Определитель матрицы
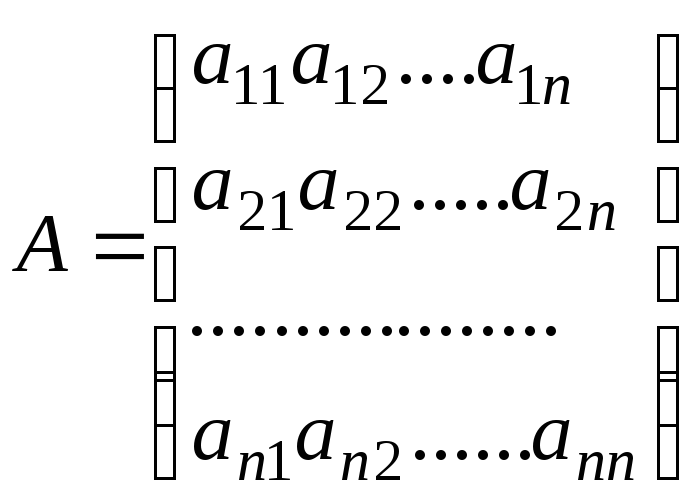 (2.1)
(2.1)
будем
обозначать
![]() ,
или
,
или
![]() ,
или
,
или
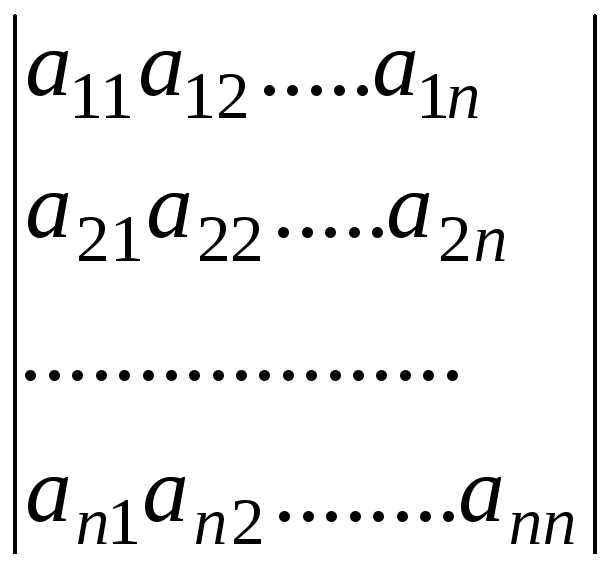 .
.
Понятие детерминанта квадратной матрицы (2.1) порядка n определим по индукции. Принцип математической индукции является одним из распространенных методов доказательств математический утверждений, а также способом определений, зависящих от натурального числа n. В применении к определениям этот принцип гласит: если какое-либо понятие сформулировано для 1 и если из допущения о введении его для натурального числа к, вытекает определение этого понятия для натурального числа к+1, то оно считается определенным для любого натурального числа n.
Определение 2.1.
1)
Детерминант квадратной матрицы
![]() первого
порядка равен числу а.
первого
порядка равен числу а.
2)
В предположении, что определен детерминант
квадратной матрицы порядка n-1,
где
![]() ,
детерминант квадратной матрицы (2.1)
порядка n
определяется формулой
,
детерминант квадратной матрицы (2.1)
порядка n
определяется формулой
![]() ,
(2.2)
,
(2.2)
где
![]() - детерминант квадратной матрицы порядка
n-1,
полученной из А
вычеркиванием первой строки и k-го
столбца.
- детерминант квадратной матрицы порядка
n-1,
полученной из А
вычеркиванием первой строки и k-го
столбца.
Для
определения чисел
![]() мы можем воспользоваться той же формулой
(2.2), поскольку она имеет место для матриц
любого порядка, большего единицы. Тем
самым мы выразим
мы можем воспользоваться той же формулой
(2.2), поскольку она имеет место для матриц
любого порядка, большего единицы. Тем
самым мы выразим
![]() через определители матриц порядка n-2.
Продолжая этот процесс, на (n-1)-ом
шаге придем к матрицам первого порядка,
а для них детерминант определяется
непосредственно.
через определители матриц порядка n-2.
Продолжая этот процесс, на (n-1)-ом
шаге придем к матрицам первого порядка,
а для них детерминант определяется
непосредственно.
Применим определение
2.1 к матрицам второго порядка. Для матрицы
![]() имеем
имеем
![]() ,
,
![]() и, следовательно, по формуле (2.2)
и, следовательно, по формуле (2.2)
![]() ,
т.е. определитель матрицы второго порядка
равен разности произведений ее элементов
на главной и побочной диагоналях.
,
т.е. определитель матрицы второго порядка
равен разности произведений ее элементов
на главной и побочной диагоналях.
Вычислим еще определитель единичной матрицы n-го порядка. С помощью формулы (2.2) находим
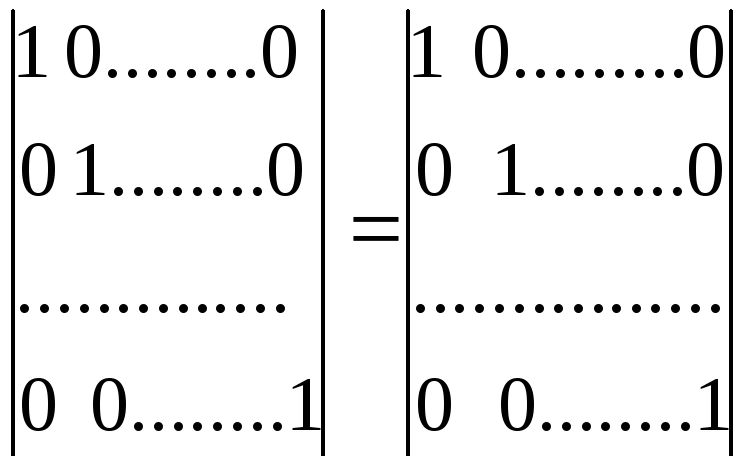 ,
,
где в правой части стоит определитель единичной матрицы (n-1)-го порядка. Применяя к этому определителю формулу (2.2), выразим его через определитель единичной матрицы (n-2)-го порядка. Продолжая этот процесс, на (n-1)-ом шаге получим равенство
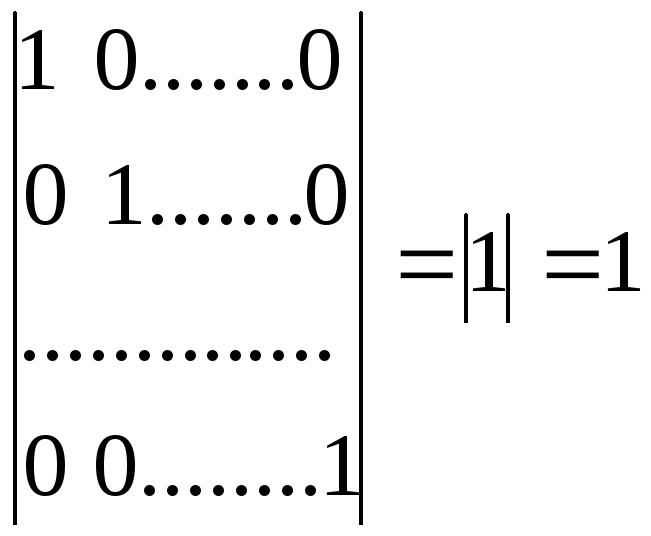 .
.
Итак,
![]() .
(2.3)
.
(2.3)
Число
![]() называется дополнительным
минором
элемента
называется дополнительным
минором
элемента
![]() .
По аналогии дополнительный минор
произвольного элемента матрицы (2.1)
определяется как детерминант матрицы,
полученной из исходной вычеркиванием
той строки и того столбца, на пересечении
которых этот элемент расположен.
Дополнительный минор элемента
.
По аналогии дополнительный минор
произвольного элемента матрицы (2.1)
определяется как детерминант матрицы,
полученной из исходной вычеркиванием
той строки и того столбца, на пересечении
которых этот элемент расположен.
Дополнительный минор элемента
![]() ,
где
,
где
![]() ,
будем обозначать
,
будем обозначать
![]() .
Далее, алгебраическим дополнением
элемента
.
Далее, алгебраическим дополнением
элемента
![]() матрицы (2.1) назовем число
матрицы (2.1) назовем число
![]() ,
определяемое формулой
,
определяемое формулой
![]() .
(2.4)
.
(2.4)
Теорема 2.1. Определитель матрицы (2.1) равен сумме произведений элементов какой-либо ее строки (столбца) на алгебраические дополнения этих элементов, т.е.
![]()
(2.5)
![]() .
.
Доказательство теоремы можно найти в [1], [2].
Формулы (2.5) называются формулами разложения определителя по строке и столбцу соответственно.
В качестве примера вычислим определитель третьего порядка
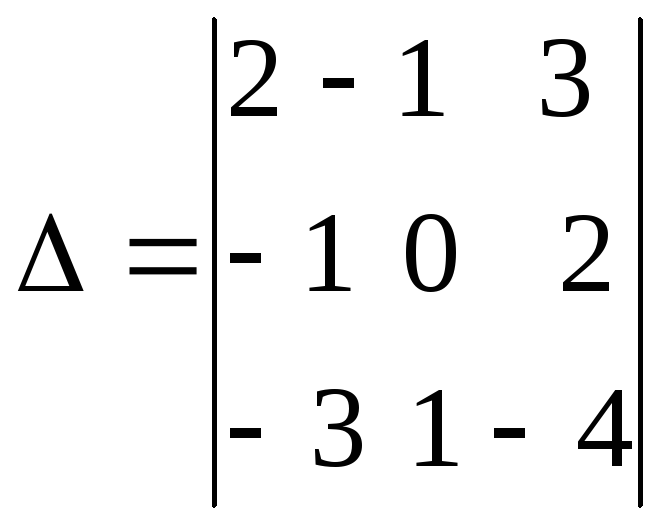 .
.
Разложим его по второй строке:
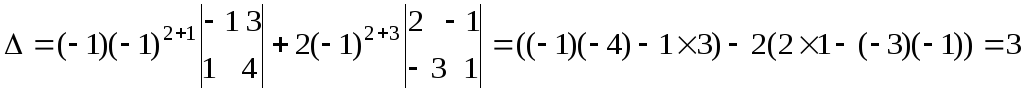 .
.
![]() Теорема
2.2. Для
любой квадратной матрицы
Теорема
2.2. Для
любой квадратной матрицы
![]() .
.
Доказательство
проведем по индукции. Для матриц первого
порядка равенство очевидно, так как при
транспонировании матрицы первого
порядка она не изменяется. Предложим,
что утверждение верно для матриц порядка
n-1
и докажем его для матриц порядка n.
Пусть
![]() - матрица, полученная из А
вычеркиванием первой строки и
- матрица, полученная из А
вычеркиванием первой строки и
![]() столбца, а
столбца, а
![]() - матрица, полученная из
- матрица, полученная из
![]() вычеркиванием
вычеркиванием
![]() строки и первого столбца. Легко видеть,
что
строки и первого столбца. Легко видеть,
что
![]() .
Отсюда по предположению индукции
.
Отсюда по предположению индукции
![]() ,
т.е. дополнительный минор элемента
,
т.е. дополнительный минор элемента
![]() в матрице А
равен дополнительному минору элемента
в матрице А
равен дополнительному минору элемента
![]() в матрице
в матрице
![]() .
Так как
.
Так как
![]() ,
то разложение
,
то разложение
![]() по первой строке совпадает с разложением
по первой строке совпадает с разложением
![]() по первому столбцу и, следовательно,
по первому столбцу и, следовательно,
![]() .
.
Из теоремы 2.2 вытекает равноправность строк и столбцов. Именно, если справедливо какое-либо утверждение о детерминантах, касающееся строк, то верно и аналогичное утверждение, касающееся столбцов. Поэтому остальные свойства определителей достаточно сформулировать и доказать только для строк.
Теорема
2.3.
Если
![]() -ая
строка
-ая
строка
![]() матрицы
матрицы
![]() есть линейная комбинация строк
есть линейная комбинация строк
![]() и
и
![]() ,
т.е.
,
т.е.
![]() ,
то
,
то
![]() где матрицы
где матрицы
![]() и
и
![]() получаются из
получаются из
![]() заменой строки
заменой строки
![]() соответственно на
соответственно на
![]() и
и
![]() .
.
Доказательство.
По определению операций над строками
для всех
![]() имеют место равенства
имеют место равенства
![]() ,
где через
,
где через
![]() и
и
![]() обозначены к-ые
элементы строк
обозначены к-ые
элементы строк
![]() и
и
![]() .
Подставляя эти равенства в разложение
.
Подставляя эти равенства в разложение
![]() по
по
![]() строке, получим
строке, получим
![]() .
.
Свойство, выраженное теоремой 2.3, носит название линейности определителя по строке. Часто линейность определителя по строке формулируется в виде двух отдельных свойств:
-
При умножении строки матрицы на число ее определитель умножается на это число.
-
Если строка матрицы есть сумма двух строк, то ее определитель равен сумме определителей соответствующих матриц.
Теорема 2.4. При перестановке местами каких-либо двух строк матрицы ее определитель изменяет знак.
Доказательство
проведем по индукции. Непосредственной
проверкой легко убедится, что определитель
матрицы второго порядка при перестановке
строк изменяет знак. Допустим, что
утверждение верно для матриц порядка
![]() ,
где
,
где
![]() и докажем его для матриц порядка n.
Определитель матрицы порядка n
разложим по любой строке, отличной от
переставляемых строк. Переставляемые
строки войдут в каждый дополнительный
минор, и поскольку утверждение верно
для матриц (n-1)-го
порядка при перестановке строк каждый
минор изменит знак. Отсюда знак изменится
и у определителя матрицы порядка n.
и докажем его для матриц порядка n.
Определитель матрицы порядка n
разложим по любой строке, отличной от
переставляемых строк. Переставляемые
строки войдут в каждый дополнительный
минор, и поскольку утверждение верно
для матриц (n-1)-го
порядка при перестановке строк каждый
минор изменит знак. Отсюда знак изменится
и у определителя матрицы порядка n.
Обратная матрица.
Определение
3.1 Матрица
![]() называется обратной
к матрице
называется обратной
к матрице
![]() ,
если
,
если
![]() ,
(3.1)
,
(3.1)
где
![]() -
единичная матрица некоторого порядка
n.
-
единичная матрица некоторого порядка
n.
Поскольку
![]() и
и
![]() перестановочны, они обе должны быть
квадратными матрицами одного и того же
порядка n.
перестановочны, они обе должны быть
квадратными матрицами одного и того же
порядка n.
Теорема
3.1. Если
у некоторой матрицы
![]() существует обратная, то она только одна.
существует обратная, то она только одна.
Доказательство.
Пусть
![]() имеет две обратные матрицы
имеет две обратные матрицы
![]() и
и
![]() .
Тогда согласно (3.1)
.
Тогда согласно (3.1)
![]() .
Умножив обе части этого равенства слева
на
.
Умножив обе части этого равенства слева
на
![]() ,
получим
,
получим
![]() или, в силу ассоциативности умножения
матриц
или, в силу ассоциативности умножения
матриц
![]() или, в силу (3.1) и (1.3)
или, в силу (3.1) и (1.3)
![]() .
.
Рассмотрим
квадратную матрицу
![]() порядка.
порядка.
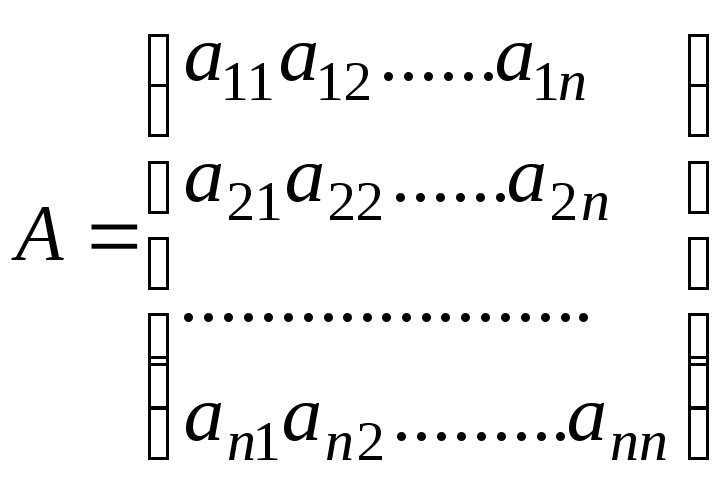 .
.
Определение
3.2. Квадратная
матрица
![]() называется невырожденной,
если ее определитель отличен от нуля.
называется невырожденной,
если ее определитель отличен от нуля.
Теорема
3.2. Для
того чтобы матрица
![]() имела обратную необходимо и достаточно,
чтобы она была невырожденной, т.е.
имела обратную необходимо и достаточно,
чтобы она была невырожденной, т.е.
(![]() имеет обратную)
имеет обратную)
![]() (
(![]() - невырожденная).
- невырожденная).
Доказательство.
1.
Необходимость.
Пусть у матрицы
![]() существует обратная
существует обратная
![]() ,
т.е. выполнено условие (3.1). Отсюда
,
т.е. выполнено условие (3.1). Отсюда
![]() или
в силу теоремы 2.7 и формулы (2.3)
или
в силу теоремы 2.7 и формулы (2.3)
![]() .
Из последнего равенства следует , что
.
Из последнего равенства следует , что
![]() ,
т.е. матрица
,
т.е. матрица
![]() невырожденная.
невырожденная.
2.
Достаточность.
Пусть матрица
![]() невырожденная,
т.е.
невырожденная,
т.е.
![]() .
.
Рассмотрим матрицу
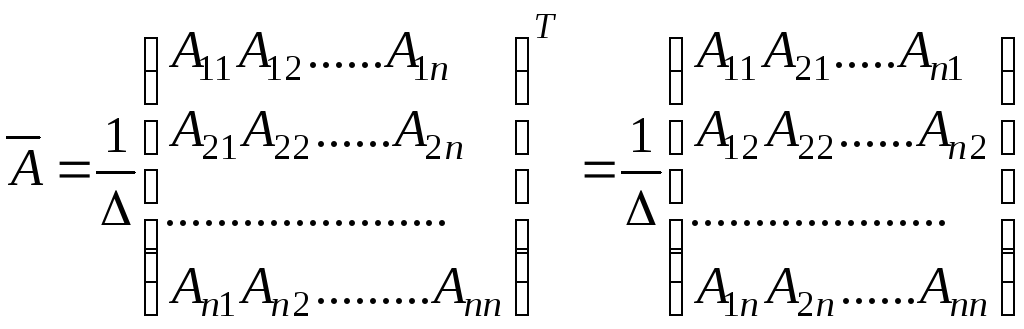 ,
,
где
![]() ,
а
,
а
![]() - алгебраическое дополнение элемента
- алгебраическое дополнение элемента
![]() матрицы
матрицы
![]()
![]() .
Покажем, что
.
Покажем, что
![]() - обратная к матрице
- обратная к матрице
![]() ,
т.е. выполнены условия
,
т.е. выполнены условия
![]() .
(3.2)
.
(3.2)
По правилу умножения матриц находим
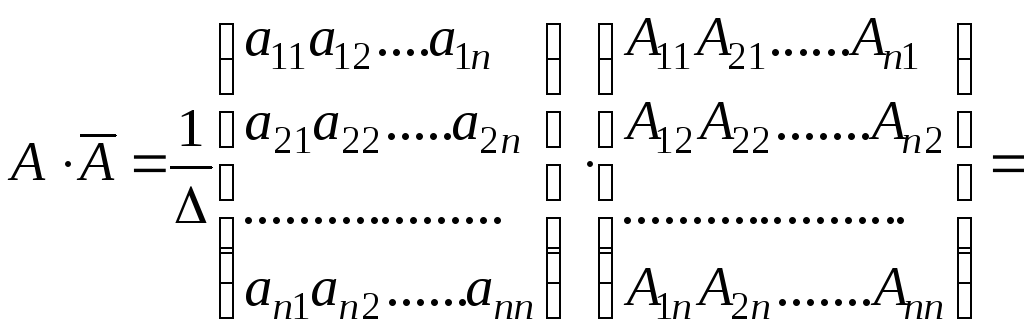
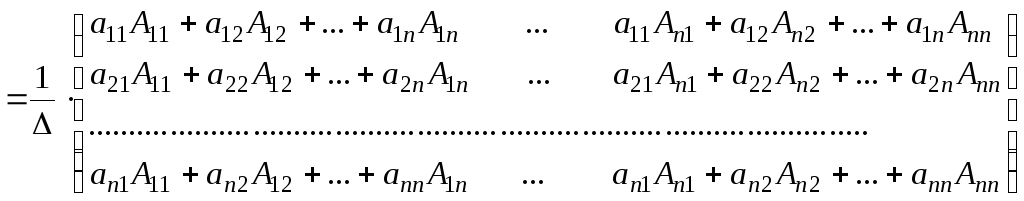
или в силу теорем 2.1 и 2.8
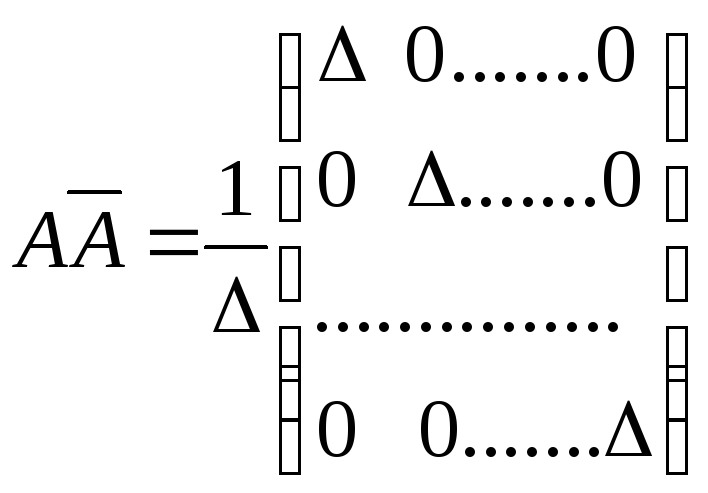 .
.
Отсюда по правилу умножения матрицы на число
 =
=![]() .
.
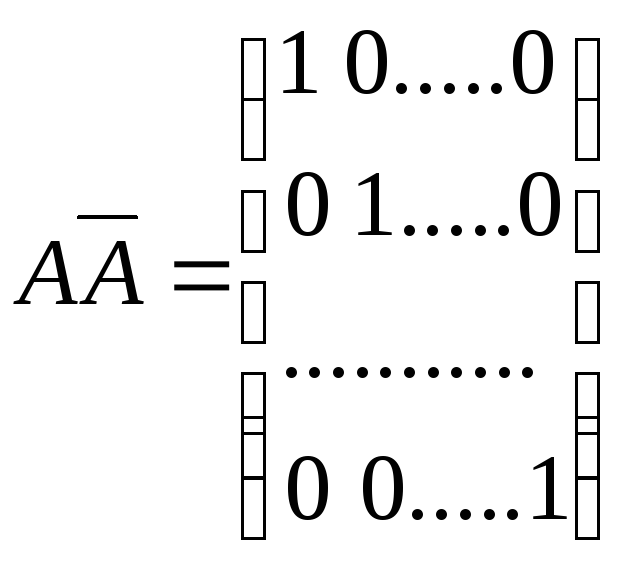
Второе из условий (3.2) проверяется аналогично.
Мы
не только доказали теорему 3.2, но и
получили явное выражение для матрицы,
обратной к матрице
![]() :
:
 .
(3.3)
.
(3.3)
При
больших размерах матрицы
![]() применение формулы (3.3) связано с очень
большими вычислениями. Проще находить
обратную матрицу с помощью элементарных
преобразований над строками матрицы.
применение формулы (3.3) связано с очень
большими вычислениями. Проще находить
обратную матрицу с помощью элементарных
преобразований над строками матрицы.
Определение 3.3. Элементарными преобразованиями матрицы называются:
-
умножение строки (столбца) на число, отличное от нуля;
-
прибавление к одной строке (столбцу) другой строки (столбца);
-
перестановка строк (столбцов).
Для
данной матрицы
![]() n-ого
порядка
построим матрицу
n-ого
порядка
построим матрицу
![]() размера n×2n,
приписывая к А
справа
единичную матрицу J
порядка n.
Далее, используя элементарные
преобразования над строками, приводим
матрицу ГА
к виду
размера n×2n,
приписывая к А
справа
единичную матрицу J
порядка n.
Далее, используя элементарные
преобразования над строками, приводим
матрицу ГА
к виду
![]() ,
что всегда возможно, если А
не вырождена. Тогда
,
что всегда возможно, если А
не вырождена. Тогда
![]() .
.
Ранг матрицы.
В
матрице А
размера
![]() выделим какие-нибудь S
строк и S
столбцов, где
выделим какие-нибудь S
строк и S
столбцов, где
![]() и
и
![]() .
Минором
порядка S
матрицы A
называется определитель квадратной
матрицы порядка S,
образованной элементами, расположенными
на пересечении выбранных строк и
столбцов.
.
Минором
порядка S
матрицы A
называется определитель квадратной
матрицы порядка S,
образованной элементами, расположенными
на пересечении выбранных строк и
столбцов.
Определение
4.1.
В матрице А
размера
![]() минор порядка r
называется базисным,
если он отличен от нуля, а все миноры
порядка r+1
равны нулю или их вообще нет, т.е. r
совпадает
с одним, из чисел
минор порядка r
называется базисным,
если он отличен от нуля, а все миноры
порядка r+1
равны нулю или их вообще нет, т.е. r
совпадает
с одним, из чисел
![]() или
или
![]() .
.
В матрице может быть несколько базисных миноров, все они имеют один и тот же порядок. Действительно, если все миноры порядка r+1 равны нулю, то равны нулю и все миноры порядка r+2, а следовательно, и все миноры больших порядков. Для доказательства достаточно применить определение детерминанта к какому-либо минору порядка r+2. Все дополнительные миноры элементов первой его строки являются минорами порядка r+1 данной матрицы и, следовательно, равны нулю.
Определение 4.2. Рангом матрицы называется порядок ее базисного минора или, иначе, наибольший порядок отличных от нуля ее миноров.
Ранг нулевой матрицы по определению считают нулем. Ранг матрицы будем обозначать rаngА.
Теорема
4.1. (о
базисном миноре).
В произвольной матрице А
размера
![]() каждая строка (столбец) является линейной
комбинацией строк (столбцов), в которых
расположен базисный минор.
каждая строка (столбец) является линейной
комбинацией строк (столбцов), в которых
расположен базисный минор.
Доказательство
проведем
для строк (утверждение теоремы для
столбцов доказывается аналогично).
Обозначим через
![]() элементы матрицы А,
а через
элементы матрицы А,
а через
![]() - ее строки. Пусть базисный минор
расположен в строках с номерами
- ее строки. Пусть базисный минор
расположен в строках с номерами
![]() и в столбцах с номерами
и в столбцах с номерами
![]() .
Надо доказать, что при любом
.
Надо доказать, что при любом
![]() существует такие числа
существует такие числа
![]() ,
что
,
что
![]() или по определению линейных операций
со строками
или по определению линейных операций
со строками
