Уравнения прямой в пространстве

Общие уравнения прямой.Рассмотрим систему двух пересекающихся плоскостей. Пусть плоскостьS₁ имеет уравнениеA₁x+B₁y+C₁z+D₁=0 , а плоскостьS₂- уравнениеA₂x+B₂y+C₂z+D₂=0. Тогда точки линии пересечения Lэтих плоскостей лежат и в плоскостиS₁ и их координаты удовлетворяют уравнению плоскостиS₁и эти точки (линииL) лежат в плоскостиS₂ и их координаты удовлетворяют уравнению плоскостиS₂. Таким образом, координаты точек прямой удовлетворяют системе уравнений

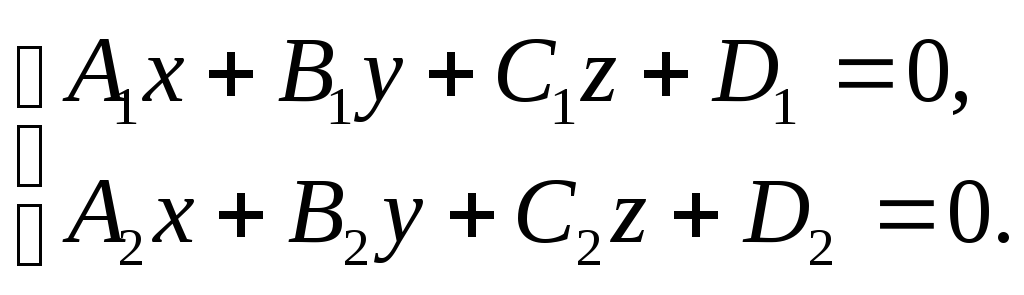(2.35)

Система (2.35) - общие уравнения прямой L – линии пересечения плоскостейSиS.

Канонические уравнения прямой имеют вид

. (2.36)

Здесь , вектор{m,n,p} параллелен прямойLи называетсянаправляющим вектором прямой (рис. 40).

Рис. 40

Параметрические уравнения прямой. Если в уравнениях (2.36) ввести новую переменную величину - коэффициент пропорциональности t:

и выразить текущие координаты прямой через эту новую переменную, то получим систему

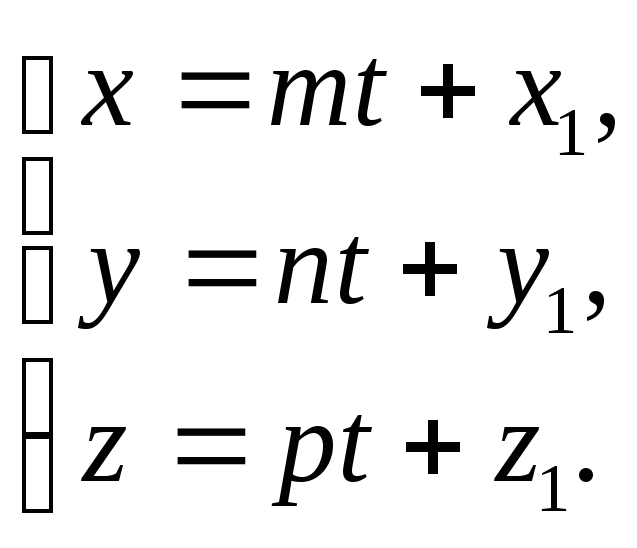(2.37)

Введенный коэффициент пропорциональности t называется параметром, а уравнения (2.37) -параметрические уравнения прямой L.Таким образом, одному значению параметраtсоответствует по (2.37) тройка чиселx, y, z, которой соответствует единственная точка пространства. Множеству значений параметра соответствует множество точек - линияL.

Уравнения прямой, проходящей через две заданных точки имеют вид

, (2.38)

где LиL.

Задачи на плоскость и прямую

Угол между двумя пересекающимися плоскостями S и S определяется по формуле

,

где S₁ иS₂заданы своими общими уравнениями соответственно A₁x+B₁y+C₁z+D₁=0иA₂ x+B₂ y+C₂ z+D₂=0.

Углы между двумя плоскостями это двугранные углы мерой которых являются соответствующие линейные углы. Нетрудно показать, что в качестве угла между плоскостями можно принять либо угол между нормальными векторами этих плоскостей , , либо угол, дополняющий угол между этими векторами до 180^о.

Условия параллельности и перпендикулярности двух плоскостей.

- Если плоскости параллельны, то их нормальные вектора коллинеарны, а тогда их соответствующие координаты пропорциональны:

- Если плоскости взаимно перпендикулярны, то их нормальные вектора ортогональны, а тогда скалярное произведение или в координатной форме:

Расстояние от точки до плоскости. Пусть точка задана координатами M₁(x₁,y₁,z₁), а плоскость S задана своим нормальным уравнением . Тогда расстояние

Следовательно, для того чтобы найти расстояние от точки до плоскости, нужно в левую часть нормального уравнения плоскости вместо текущих координат подставить координаты рассматриваемой точки и полученный результат взять по абсолютной величине. Если плоскость задана общим уравнением, то сначала следует его привести к нормальному виду и тогда

,

где и знак уNвыбирается противоположным знаку свободного членаD в общем уравнении плоскости.

Угол между прямой и плоскостью.Угломмежду прямойL и плоскостьюS является угол между прямой и ее проекцией на плоскость (рис. 41).

Пусть плоскость задана общим уравнением , а прямая

каноническими уравнениями Тогда=90⁰-и

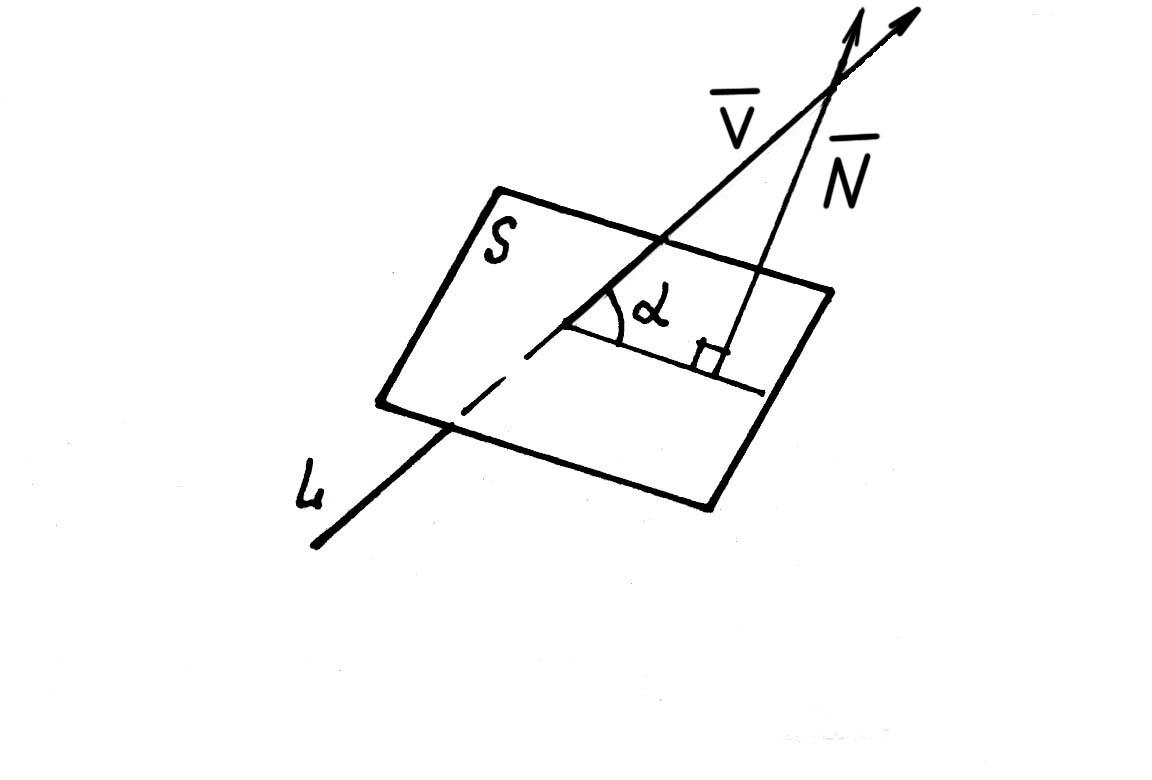
Рис. 41

Условия параллельности и перпендикулярности прямой и плоскости:

если LS, то и тогдаилиAm+Bn+Cp=0 ;

если LS, тои тогда