Некоторые задачи на прямую

Угол между двумя прямыми L₁ и L₂ есть угол , на который нужно повернуть прямуюL₁ до совмещения с прямой L₂ , вокруг точки их пересечения, вращая ее против хода часовой стрелки.

Рис. 18

Из приведенного определения следует, что угол между прямой L₁ и прямой L₂ есть , а угол между прямымиL₂ и L₁ есть (рис.18) и. Для угла между двумя любыми прямыми справедливо соотношение . Если прямые заданы своими уравнениями с угловыми коэффициентами L₁ - y=k₁x+b₁; L₂ - y=k₂x+b₂ , то

, . (2.10)

Условия параллельности и перпендикулярности двух прямых.

Если L₁ L₂ , то k₁ =k₂ .

Если L₁  L₂ , то

Расстояние от точки до прямой.

Если прямая L задана своим нормальным уравнением: , а точка - своими координатами, то- расстояние от точки до прямой L будет

. (2.11)

Таким образом, чтобы найти расстояние от точки до прямой L, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точкии полученный результат взять по абсолютной величине.

Если прямая линия задана своим общим уравнением, то искомое расстояние определится по формуле

. (2.12)

Аналитическая геометрия в пространстве Понятие об уравнениях поверхностей и линий в пространстве

Пусть задана пространственная прямоугольная система координат XYZ с началом в точкеO . Рассмотрим уравнение

. (2.28)

Координаты точки М(x,y,z) удовлетворяют уравнению (2.28), если при подстановке чиселx, y, z в это уравнение оно превращается в верное равенство. Каждой тройке чисел, удовлетворяющей уравнению (2.28) в выбранной системе координат, соответствует точка. Множеству троек чисел(x,y,z)удовлетворяющих уравнению (2.28) соответствует множество точек, геометрическое место точек - поверхностьS. При этом точки, координаты которых удовлетворяют уравнению (2.28), принадлежат поверхности S, а точки, координаты которых не удовлетворяют уравнению (2.28), не принадлежатS .

Уравнение (2.28) называется уравнением поверхности Sв заданной системе координат, если этому уравнению удовлетворяют координаты тех и только тех точек, которые принадлежат поверхностиS.

Графиком уравнения(2.28) называется поверхностьS, текущие координаты которой связаны данным уравнением.

Линия в пространственной системе координат рассматривается как линия пересечения двух поверхностей, т.е. как множество точек одновременно принадлежащих как одной поверхности, так и другой поверхности. Если F₁ (x,y,z)=0 и F₂ (x,y,z)=0 уравнения двух поверхностей, соответственно S₁ и S₂ , пересечением которых является данная линия L, то координаты точек, лежащих на линии L , удовлетворяют обоим уравнениям поверхностей S₁ и S₂ и обоим указанным уравнениям не удовлетворяют координаты точек, не лежащих на линии L.

Таким образом, уравнения

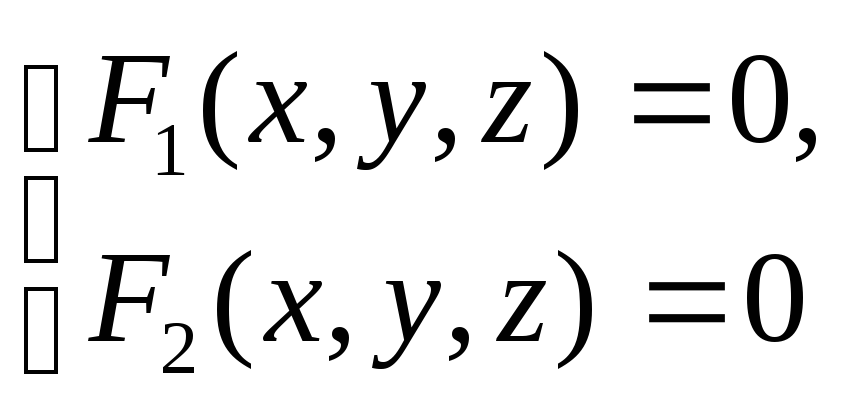(2.29)

совместно определяют линию L, т.е. система (2.29) является уравнениями линииL.