-
Линейная корреляция.
Для вычисления
коэффициентов
и
прямой регрессии (3.1) часто используют
коэффициент линейной корреляции
.
Пусть имеется
выборка
объёма
.
Напомним, что выборочная ковариация
определяется равенством
,
(5.1)
где
,
– выборочные средние;
– выборочное среднее произведения.
Выборочные дисперсии определяются соотношениями:
;
.
(5.2)
По определению выборочный коэффициент корреляции
.
(5.3)
Рассмотрим систему
(3.3). Разделив все её слагаемые на
,
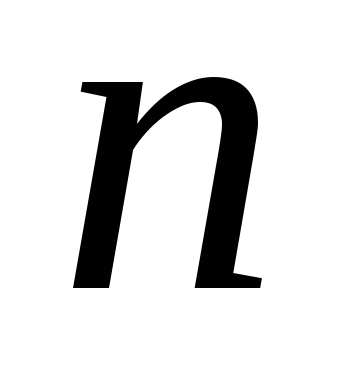получим эквивалентную систему:
Отсюда по формулам Крамера
;
.
Подставив
коэффициенты
и
в уравнение регрессии
,
получим
или с учётом равенства (13)
.
Итак, уравнение
прямой регрессии
на
имеет вид
.
(5.4)
Аналогично найдём,
что уравнение прямой регрессии
на
запишется в виде
.
(5.5)
Из уравнений (5.4)
и (5.5) следует, что прямые регрессии
на
и
на
проходят через точку
.
Эти прямые совпадают, когда
.
Величины
и
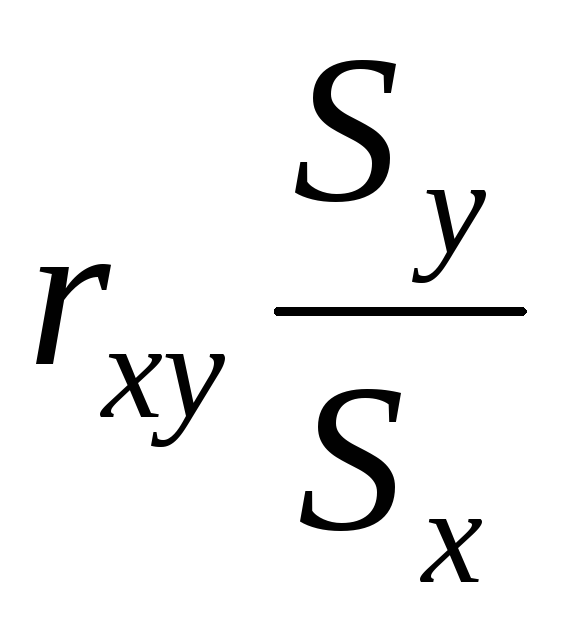называются коэффициентами
линейной регрессии и
обозначаются:
;
.
(5.6)
Перемножив правые
и левые равенства (5.6), после извлечения
корня получим
,
т.е. коэффициент корреляции есть среднее
геометрическое коэффициентов линейной
регрессии.
Замечание.
Если
,
то обычно не стоит использовать линейную
функцию. В этом случае можно попробовать
найти нелинейную функцию, например,
квадратичную функцию
,
коэффициенты которой вычисляют также
методом наименьших квадратов.