Оптимизация на основе теории бинарных отношений

В практике принятия решения важной является проблема выбора между вариантами решений, уже сгенерированными специалистами в конкретной области. Множество сгенерированных решений X будем называть множеством выбора, а его элементы x_i альтернативами или вариантами. Как правило, это множество конечно:

Одним из подходов к решению проблемы выбора является использование мнений специалистов – экспертов.

В данной теме мы будем рассматривать следующий механизм выбора: предложим эксперту попарно сравнить альтернативы. Математически это сводится к построению некоторого бинарного отношения (БО) между альтернативами множестве выбора.

Какими свойствами должно обладать бинарное отношение (БО), построенное экспертами, чтобы оно помогло ЛПР осуществить обоснованный выбор? Для ответа на этот вопрос напомним основные свойства, которые полезны при обосновании выбора.

Отношение ρ

1. симметрично , если,

2. антисимметрично, если ,

3. асимметрично, если .

Отношение строгого упорядочения

Минимальным требованием, предъявляемые к БО для выбора, является асимметрия. Это БО называется отношением строгого упорядочения. Строгое упорядочение асимметрично и антирефлексивно.

Данное отношение все же не может обеспечить качественный выбор, например оно не полно и даже не является слабополным. Последнее означает, что некоторые пары не попали в БО и эксперт не смог их сравнить.

У этого может быть 3 причины:

1. он считает, что они неразличимы,

2. он не уверен, что одна из альтернатив превосходит другую,

3. он считает, что они несравнимы.

Пары, не попавшие в асимметричное отношение, тоже определяют БО. Такое отношение называется отношением безразличия или отношением толерантности.

,

где Р – отношение строгого упорядочения, I – индуцированное им отношение толерантности.

Объединив пары P и I, получим отношение не строгого упорядочения:

,

оно уже, по крайней мере, слабополно.

Свойства отношения толерантности.

• Отношение , которое включает те и только те пары множестваX, которые не попадают в отношение R называются дополнительными по отношению к R:

.

• Отношение 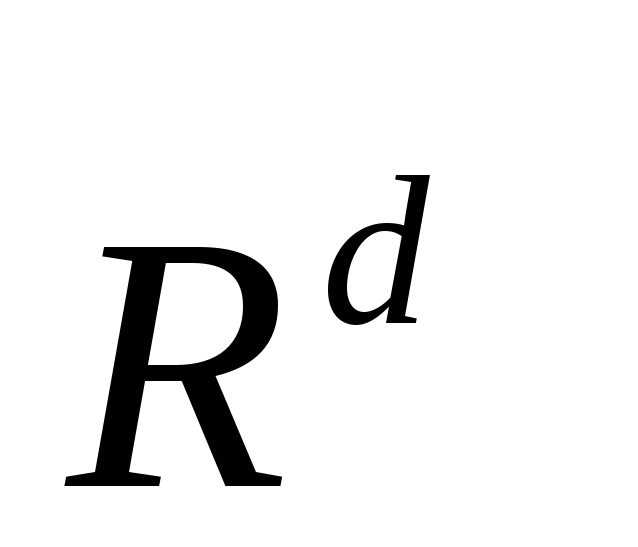, дополнительное к обратному, называется двойственным по отношению кR:

.

Теорема:

Отношение строгого упорядочивания P и не строгого упорядочивания R образуют двойственную пару: .

Теорема:

Слабые и сильные порядки

К требованию асимметрии целесообразно добавить одно из следующих свойств: негатранзитивность или транзитивность.

1. Транзитивность:

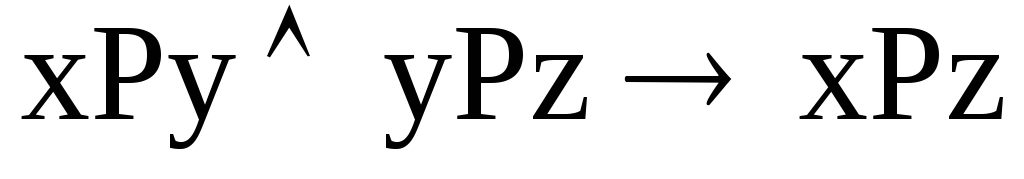
2. Негатранзитивность:

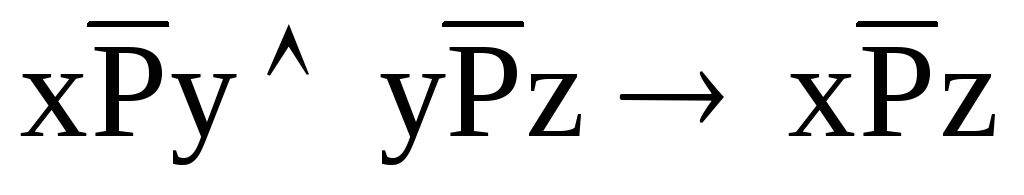
Слабый порядок - асимметричное негатранзитивное отношение или строго упорядоченное и негатранзитивное (пример: x>y).

Так же как и для строгого упорядочения можно ввести отношение безразличия для слабого порядка:

Отношение безразличия для строгого упорядочения было рефлексивно и симметрично. Новое отношение безразличия, введенное для слабого порядка, является кроме этого и транзитивным.

Докажем теорему:

Отношение является транзитивным.

- рефлексивно, симметрично, транзитивно и следовательно является отношением эквивалентности. Это означает, что по основному свойству отношения эквивалентности множество альтернатив X разбивается на взаимно непересекающиеся классы эквивалентности, которые в данном случае являются классами взаимно толерантных элементов.

.

- фактор-множество, множество классов эквивалентности.

Указанные выше 3 свойства уже позволяют сравнивать не отдельные элементы множестваX, а целые классы.

Введем отношение :

Это отношение читается так: класс превосходит класс)

Это определение вводит отношение , которое вызвано отношением слабого порядка. В этом определении безразлично какойx из и какойy из были взяты, в любом случае если для одной такой пары имеет местоxPy, то оно будет иметь место и для любой другой такой пары.

Отношение называется сильным порядком.Сильный порядок – асимметричное, негатранзитивное, слабо-полное отношение.

Слабая полнота: для любой пары .классов иимеет место

Замечание. Подобного отношения нельзя ввести для отношенияI, введенного для строгого упорядочивания

Таким образом, отношение удается ввести только благодаря негатранзитивности отношенияP, которое добавили.