Нечеткое отношение предпочтения

Нечетким отношением нестрого предпочтения на множестве альтернатив X называется любое, заданное на X рефлексивное отношение.

Исходя из этого отношения  можно построить 3 отношения, связанных с ним:

1. Отношение безразличия ^I:

. Для элементов:

2. Отношение эквивалентности ^e.

Для элементов:

3. Отношение строго предпочтения ^S.

Для элементов:

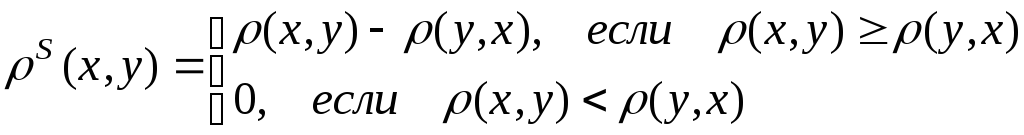
Свойства, построенных отношений:

1. ^I и ^e являются рефлексивными и симметричными.

2. ^S антирефлексивно и антисимметрично.

3. если  транзитивно, то ^e и ^S транзитивны.

Нечеткое множество недоминируемых альтернатив.

Рассмотрим отношение строго предпочтения . Используя это отношение, мы можем построить нечеткое множество недоминируемых альтернатив . Данное множество можно считать нечетким аналогом множества Парето.

Зафиксируем x. Тогда ^S(y, x) будет функцией y , которую можно рассматривать как функцию принадлежности некоторого множества Д(x) доминант элемента x. ^S(y, x) характеризует степень предпочтительности альтернативы y по сравнению с альтернативой x.

Поскольку нас интересует насколько альтернатива x недоминируема, то нам необходимо построить множество, дополнительное к Д(x), то есть

.

Его функция принадлежности будет:

.-

степень принадлежности некоторого элемента y к недоминантам x, т.е. к множеству .

Нас интересуют те x, которые минимально доминируемы, поэтому построим пересечение всех множеств .

Мы построили множество недоминируемых альтернатив с функцией принадлежности

.

В это множество входят все альтернативы, но с различной степенью принадлежности. Чем больше , тем с большим основанием можно считать данный x недоминируемым. Обычно нас интересуют одна или несколько максимально недоминируемых альтернатив, то есть

.

Пример. Пусть базовое множество альтернатив состоит из 4-х элементов x₁, x₂, x₃, x₄

Пусть построенное экспертами нечеткое отношение нестрого предпочтения и соответствующее ему отношение строго предпочтения имеют вид:

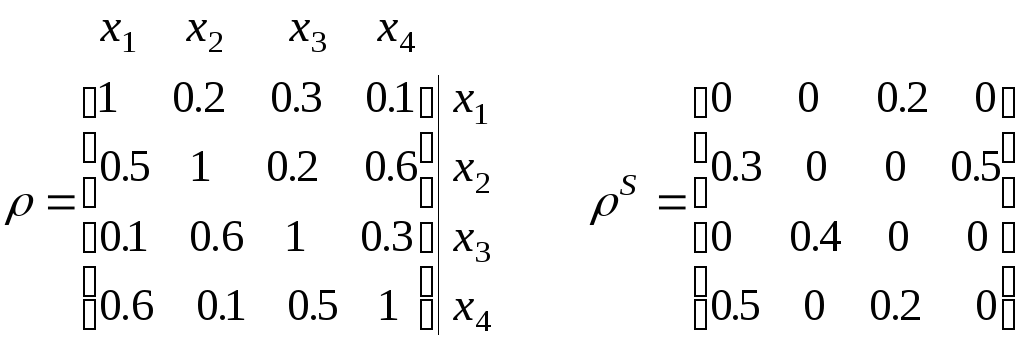
Выполнив расчеты по приведенным формулам находим множество недоминируемых альтернатив

Итак, максимально недоминируемой альтернативой является x₃, которая и рекомендуется к выбору..

Перейдем ко второму применения теории НМ.

В первой части курса в разделе многокритериальных задач мы рассматривали метод многокритериального выбора, называемого методом исследования пространства параметров (МИПП). Основным результатом МИПП является построение следующего подмножества X паретовского множества P, которое ниже будем называть множеством выбора:

. (1)

Здесь  значение iго критерия на варианте выбора x,  предельное значение этого критерия, которое еще устраивает ЛПР. Значение можно назвать границей притязаний по i–му критерию.

По приведенному определению множество X является четким. В этом ограничении заключается возможность обобщения метода.

Действительно, можно обратить внимание на две особенности множества X. Во-первых, при определении границ притязаний ЛПР ориентируется на значения критериев, которые могут быть заданы с некоторой погрешностью.

Во-вторых, сами границы притязаний задаются с определенной степенью субъективности. Оба эти обстоятельства противоречат четкости множества X.

Все варианты выбора, не попавшие в X, раз и навсегда исключаются из процесса принятия решения независимо от близости к его границам. При этом преимущество, которое получают перед ним те варианты, которые попали в множество X, и находящиеся так же близко к его границам, не выглядит достаточно обоснованным.

Целесообразно строить множество X как нечеткое, связывая размытость его границ с указанными выше неточностью задания значений критериев и субъективностью границ притязаний. Рассмотрим метод, позволяющий учесть одновременно оба указанных фактора.

Предложим ЛПР на этапе построения множества выбора указать каждому критерию две границы: границу притязаний и критическую границу . Отличие границы от ранее рассмотренной в том, что выполнение условия

означает безусловное выполнение требований ЛПР по i–му критерию с учетом неточности в определении значения и возможном изменении в его предпочтениях.

Смысл критической границы состоит в том, что все варианты выбора , для которых

,

безусловно не удовлетворяют требованиям ЛПР по i–му критерию.

Для вариантов выбора , для которых

,

степень выполнения требований ЛПР целесообразно считать тем большей, чем ближе к границе притязаний.

Обозначим указанную степень выполнения требований ЛПР по i–му критерию для варианта через . Определим ее величину так:

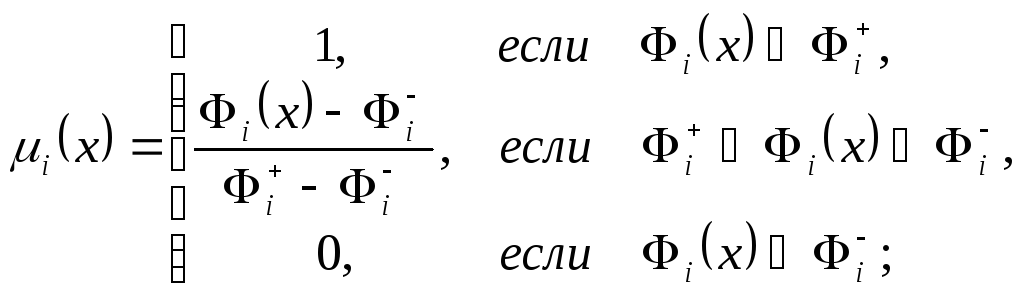(2)

По сравнению со случаем, когда X задано четко, введенная величина , дает более гибкий подход к построению множества выбора, чем даваемый формулой (1). Нетрудно заметить, что величина может быть интерпретирована как функция принадлежности альтернативы x к нечеткому множеству альтернатив, удовлетворяющих требованию ЛПР по -му критерию.

Это позволяет построить нечеткое множество решения задачи выбора, как пересечение нечетких множеств альтернатив, удовлетворяющих требованию ЛПР по каждому из критериев. Для этого , следуя принципу Заде: определим его функцию принадлежности по формуле

.

Одновременно с такой трактовкой функции , ее можно рассматривать как естественный метод унификации критериев.