Действия над нбо

С НБО можно производить все действия, которые мы определили для НМ.

В частности, функции принадлежности для объединения и пересечения двух НБО задаются формулами

.

Композиция нечетких бинарных отношений:

Обобщая формулу для композиции четких БО для НБО получим максиминную формулу для композиции двух НБО :

Пример.

Найдем композицию двух НБО

и

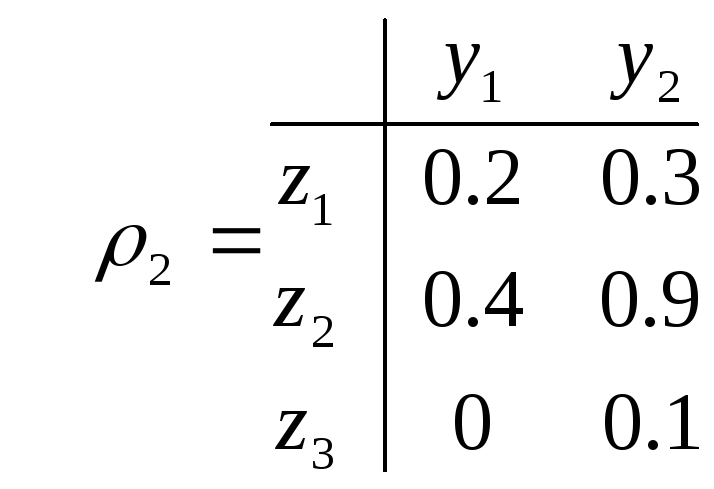
Подучим

.

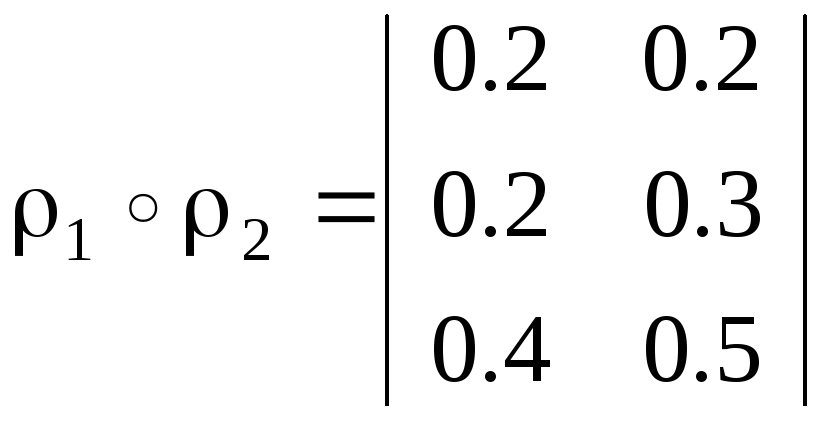Бинарное отношение Е называются диагональным или единичным, если оно задается единичной матрицей.

.

Обратное бинарное отношение

Отношение, обратное к отношению , имеет функцию принадлежности

.

Этому отношению соответствует матрица, транспонированная к матрице .

Будем говорить, что отношение тогда и только тогда, когда .

Свойства бинарных отношений:

1. Рефлексивность. Отношение называется рефлексивным, если оно содержит единичное отношение, то есть .

На языке элементов это значит, что

.

2. Слабая рефлексивность:

.

3. Сильная рефлексивность:

.

4. Антирефлексивность;

.

5. Слабая антирефлексивность:

.

6. *Сильная антирефлексивность.

7. Симметричность означает, что .

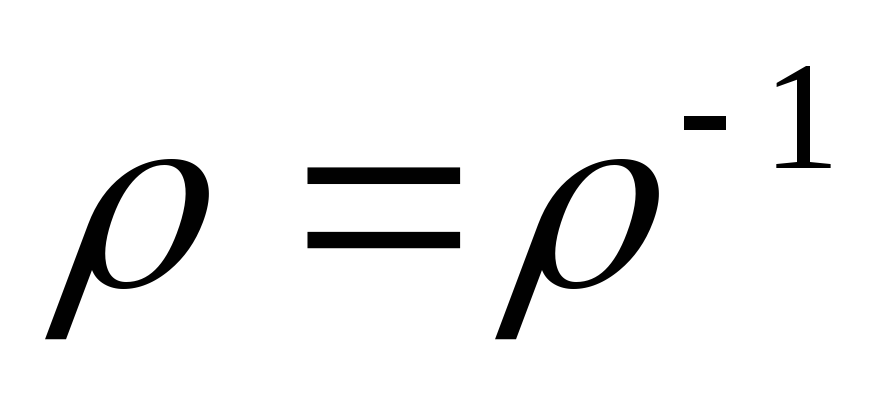На языке элементов это значит, что

.

8. Антисимметричность означает, что

.

На языке элементов

.

9. Асимметричность означает, что

На языке элементов

.

10. Сильная полнота:

.

11. *Слабая полнота:

12. Транзитивность:

На языке элементов

α уровень бинарного отношения – это четкое бинарное отношение, которое имеет следующую функцию принадлежности:

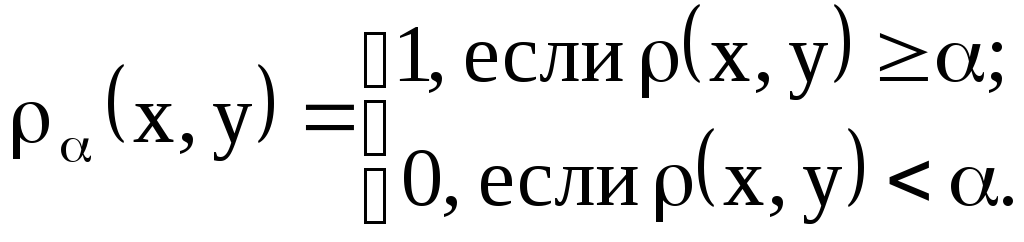
Теорема 1.

Все выше перечисленные бинарные отношения, не отмеченные знаком (*), являются таковыми вместе с любым своим α- уровнем

Как и для НМ, имеет место теорема о декомпозиции НБО

Теорема 2. Для любого НБО имеет место следующая формула:

Транзитивное замыкание нечеткого бинарного отношения

Пусть дано нечеткое бинарное отношение. Обычно оно задается экспертным образом. Для решения большинства задач ТПР оно обязано быть транзитивным Однако из-за естественных ошибок экспертов оно может оказаться нетранзитивным. Возникает задача минимальным образом подправить это отношение так, чтобы оно стало транзитивным. Эта задача решается с помощью операции транзитивного замыкания.

Дадим два вспомогательных определение.

1. Если то говорят, что ρ₂ есть расширение ρ₁.

2. k-я степень отношения задается рекурсивно:

, , .

Транзитивным замыканием для отношения ρ называется минимальное транзитивное расширение, то есть такое транзитивное отношение, для которого выполняются следующие два условия.

1. , то есть расширение .

2. Любое транзитивное отношение, являющееся расширением , является расширением .

Как выполнить транзитивное отношение?

Имеют место следующие формулы.

1. В общем случае ;

2. Если базовое множество конечно, то есть , то .

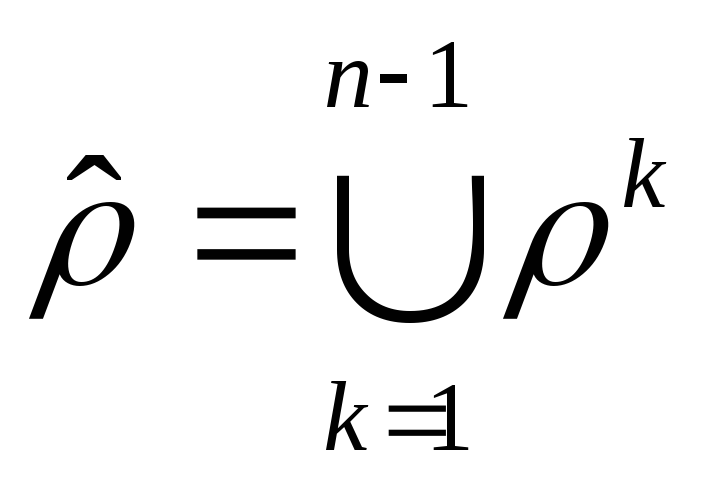3. Если базовое множество конечно и рефлексивно, то .

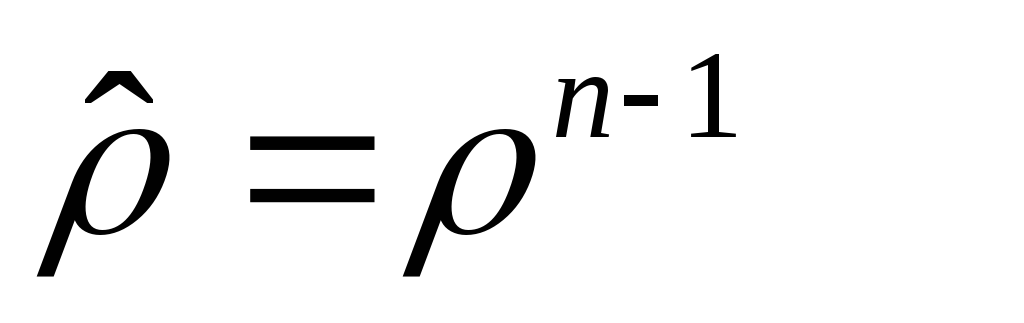Где применяются НМ и НБО?

Чаще всего НБО применяется в задачах классификации и выбора.

Для ТПР более характерны задачи выбора.

Рассмотрим два метода выбора, основанные на теории НМ и НБО.