Применение метода ветвей границ к решению задачи о коммивояжере

Ослабленной задачей для ЗК выбираем ЗН.

Решив ЗН с помощью вспомогательной процедуры, проверяем, выполняется ли для ее решения условие, что матрица решенийне имеет подциклов.

Наличие подциклов означает следующее.

Последовательность городов i₁, i₂,..., i_n, задаваемая матрицей , такова, что она распадается на два или более подциклов вида:j₁, j₂,..., j_k; k<n , причем i₁=F( i_k ).

Главным здесь является построение процедуры ветвления. Один из подходов состоит в следующем.

Пусть у текущего решения ослабленной задачи не выполняется условие С, то есть решение распадается на подциклы. Выберем подцикл с наименьшим количеством звеньев. Каждому звену такого подцикла сопоставим новую задачу о назначении, в которой вместо старого значения расстояния между городамииположим=. Это условие исключает попадание звенав оптимальное решение соответствующей задачи. Это делается для того, чтобы в дальнейшем у нас не возникало оптимальное решение с указанным подциклом. Наикратчайший цикл берется для того, чтобы количество ветвей было минимальным, так как разветвление будет содержать столько задач, сколько звеньев в кротчайшем подцикле.

В результате мы получим ряд задач, объединение допустимых решений которых совпадают с множеством допустимых решений ветвимой задачи, кроме ее оптимального решения, которое нам не подходит.

Понятие об- оптимальном решении задачи о коммивояжере

Иногда вовсе необязательно решать задачу абсолютно точно, а достаточно найти решение, оптимальное значение целевой функции которого отличается от точного не более, чем на заданное число . Это может значительно сократить трудоемкость решения.

Заметим, что оптимальное решении задачи о коммивояжере всегда не больше оптимального решения соответствующей задачи о назначении(см. рисунок).

Итак,

.

Зададимся числом и решим задачу о назначении для данной задачи о коммивояжере, получив значение. Далее, реализуя метод ВГ, будем следить за текущим значением рекорда. Если на некотором шаге этот рекорд окажется левее точки , то есть будут выполнять неравенства

,

то мы можем утверждать, что

.

Это означает, что текущий рекорд отличается по значению целевой функции от оптимального решения задачи о коммивояжере меньше, чем на . На этом решение считается найденным.

Такое решение называется - оптимальным решением задачи о коммивояжере.

Общая схема ветвления для целочисленной задачи лп

Пусть имеем целочисленную ЗЛП.

Систему уравнений-ограничений запишем в матрично-векторной форме

Целевая функция имеет обычную форму

Естественные ограничения запишем в новой форме

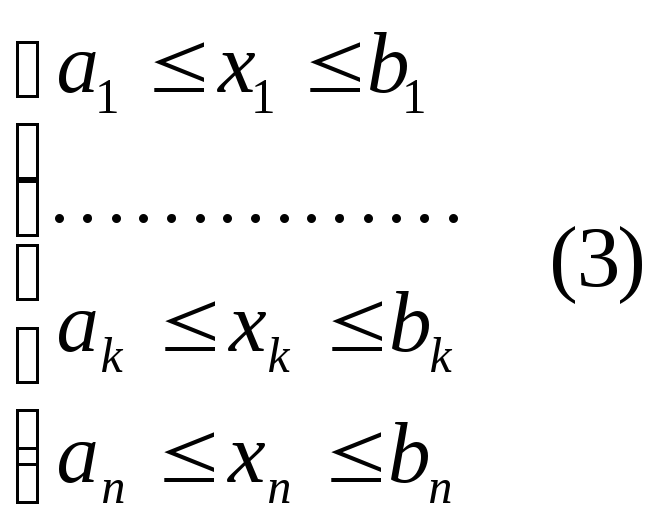
Здесь, как обычно, левые границы интервалов могут быть равны 0, а правые определяются физическими условиями задачи.

Наконец, мы имеем требование целочисленности всех или части компонент решения.

В данном случае ветвление в пункте 6 алгоритма метода ВГ можно проводить так.

Сняв требование целочисленности получим задачу L. Решим ее симплекс-методом

Пусть полученное оптимальное решение нецелочисленное, то есть хотя бы одна из координат, например, х_к не является целым числом.

Обозначим через [x_k] – целую часть х_к .

Теперь вместо только что решенной задачи построим два разветвления следующим образом.

В обеих ветвях целевую функцию и условия (1) оставим прежними. Оставим прежними и все неравенства (3) кроме k-го.

В первой задаче заменим это неравенство на неравенство

а во 2-я задаче – на неравенство

,

где

.

Итак, вместо задачи L получили две задачи (L^/) и (L^//). При этом мы выбросили отрезок (), который явно не содержит целых чисел. На этом процедура ветвления заканчивается.

Очевидно, что в данном случае дерево задач будет бинарным.