19

Среднеквадратическое приближение функции.

Рассмотрим задачу наилучшего среднеквадратичного приближения функции полиномом по системе .

Определение 1.

Обобщенным полиномом порядка m по системе {_k} называется линейная комбинация

где C_k – произвольные вещественные коэффициенты.

Задача. Найти полином , наименее уклоняющийся от функции f в метрике L₂, т.е. удовлетворяющий условию:

Теорема 1.

Если система линейно независима, то задача наилучшего среднеквадратичного приближения по этой системе однозначно разрешима.

Запишем квадрат расстояния между функцией и полиномом:

(1)

Очевидно, что величина - неотрицательно определенная квадратичная функция переменных , а такая функция достигает минимального значения. Таким образом, решение задачи среднеквадратичного приближения существует.

Докажем единственность решения.

Запишем необходимые условия минимума:

, i=0,…,m.

Вычисляя частные производные по c_i выражения (1), получим линейную cистему уравнений:

(2)

Система (2) называется нормальной системой.

Выпишем определитель этой системы

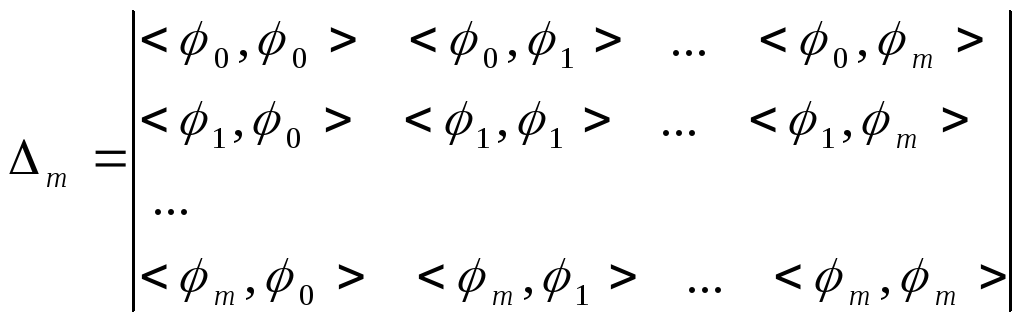(3)

Определитель системы (3) – так называемый определитель Грама системы . Известно, что если система - линейно независима, то определитель 0 (легко доказывается от противного). Согласно условию теоремы 0 и система (2) имеет единственное решение.

1.6. Классические ортогональные многочлены и их применение в задачах приближения функций.

Пусть H- гильбертово пространство со скалярным произведением <f,g> и, соответственно, нормой . Важным примером такого пространства является так называемое пространство - пространство функций f(x), для которых конечен интеграл:

(1)

Здесь h(x)- так называемая весовая функция, удовлетворяющая условиям:

1. h(x)0 на [a,b].

2. Если промежуток [a,b]- конечный, то 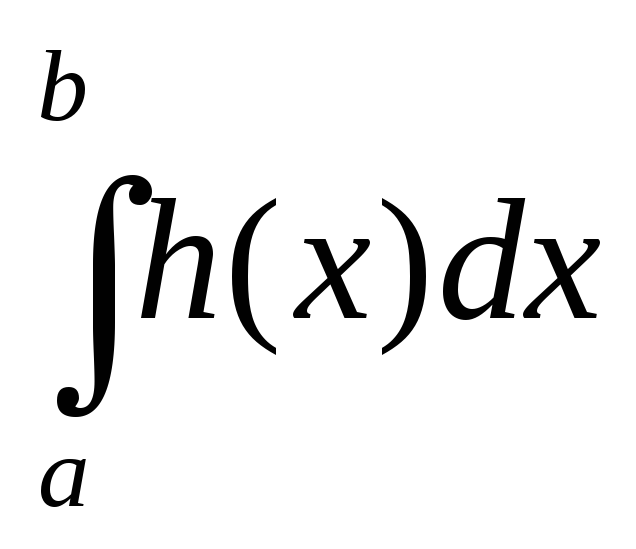существует и конечен;

Если же [a,b]=(0,+), то должно выполняться условие:

т.е. должны существовать любые моменты весовой функции.

Определение 1.

Для определено скалярное произведение:

(2)

и соответственно норма:

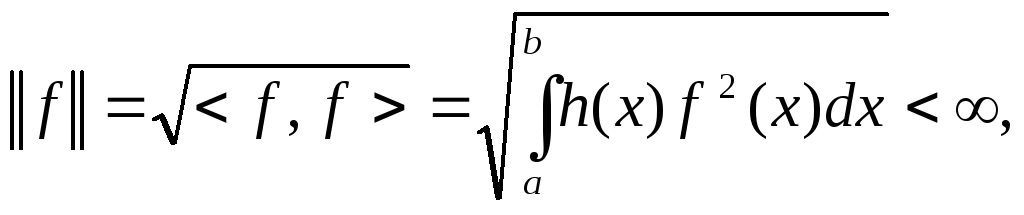
согласно условию (1).

Используя неравенство Коши – Буняковского - Шварца, получаем

Поэтому скалярное произведение существует для

Определение 2.

Расстояние между элементами f и g определяется равенством:

.

Возникает вопрос о том, как понимать нулевой элемент. Если норма , следует ли отсюда, что f=g? Вводится терминология: f=g почти всюду, то есть они могут отличаться в конечном числе точек.

Определение 3.

f и g ортогональны на отрезке [a,b] с весом h(x), если <f,g>=0 (кратко пишут ).

Если в гильбертовом пространстве взять любую линейно независимую систему , i=0,1,2,…, то ее можно ортогонализировать.

Рассмотрим в качестве примера систему: При конечный набор степенных функций линейно независим, поэтому на базе этой системы можно построить ортогональные полиномы. Известна следующая рекуррентная процедура ортогонализации (процедура Грама - Шмидта):

(3)

Коэффициенты b_k+1,j определяются из условий ортогональности:

Последовательно умножая (3) на получаем

(4)

Пример 1.

Пусть h(x)1, [a,b]=[-1,1].

Построить первые три ортогональных полинома по процедуре (3) - (4).

Далее имеем:

,

следовательно,

Действуя, аналогично далее, получаем:

Для системы ортогональных многочленов на отрезке [-1,1] с весом h(x)=1 справедлива формула Родрига:

(5)

Из (5) последовательно получаем:

и т.д.

Получаемые таким образом полиномы называются полиномами Лежандра.

Замечание.

Найденные по процедуре (3) – (4) ортогональные многочлены могут лишь множителями отличаться от тех, которые строятся по явной формуле Родрига (5).

Квадрат нормы у этих полиномов равен:

То есть эти многочлены не нормированы, так как

Для всех классических многочленов существует рекуррентная формула. Для полиномов Лежандра она имеет следующий вид:

(6)

Пусть Рассмотрим среднеквадратичное приближение:

где - среднеквадратичная ошибка аппроксимации,

- отрезок ряда Фурье для функции f(x) по системе ортогональных многочленов {P_k(x)}.

В силу ортогональности многочленов Лежандра, система нормальных уравнений (2) из §1.5 становится диагональной, и ее решение приводит к следующим выражениям для коэффициентов c_k:

(7)

При этом

то есть обеспечивается минимум нормы в L₂.

Распишем подробно ошибку аппроксимации

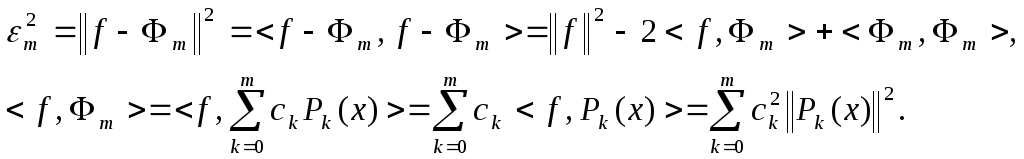(8)

С другой стороны

в силу ортогональности.

Подставляя в (8), получим

. (9)

Пример 2.

Пусть f(x)=|x|.

Аппроксимировать f(x) на [-1,1] в среднеквадратичном многочленом второй степени. Вычислить среднеквадратичную ошибку.

Используем ортогональную систему Лежандра:

Коэффициенты c_k находим по формуле (7), учитывая вид полиномов Лежандра:

Далее вычисляем среднеквадратичную ошибку по формуле (9):

1.7. Некоторые общие свойства ортогональных полиномов.

1. Многочлен P_n(x) ортогонален любому алгебраическому многочлену m-ой степени M_m(x) при m<n.

M_m(x) можно единственным образом представить в виде линейной комбинации многочленов Лежандра:

(10)

Равенство (10) тождественное, поэтому коэффициенты a_k единственным образом вычисляются путем приравнивания коэффициентов при старших степенях. Умножая обе части (10) на P_n(x), имеем

в силу ортогональности системы

2. Полином P_n(x) имеет на отрезке [-1,1] ровно n действительных и различных корней.

Заметим, что в силу теоремы Гаусса многочлен P_n(x) не может иметь более чем n корней (вообще говоря, комплексных). Пусть P_n(x) имеет меньше, чем n простых действительных корней. Обозначим их По этим точкам построим фундаментальный многочлен

Рассмотрим многочлен: - многочлен степени (k+n), который имеет нули четной кратности. Значит, новый многочлен сохраняет знак при переходе через эти нули, т.е. сохраняет знак на [-1,1]. Отсюда следует, что

Но это противоречит свойству 1, так как P_n(x) обязательно должен быть ортогонален M_k(x).

3. Между двумя соседними нулями многочлена P_n(x) лежит ровно один нуль многочлена P_n-1(x).

Доказывается по индукции с помощью рекуррентного соотношения (6).

4. При n- четном многочлен P_n(x) – четная функция от x, при n- нечетном, P_n(x) – нечетная функция от x.

Наряду с многочленами Лежандра классическими ортогональными многочленами называют следующие системы многочленов (далее (a,b) – промежуток ортогональности, r(x) – весовая функция).

1) Многочлены Якоби {Р_п ^(l,m)(х)} — при а = —1, b = 1 r(х) = (1—х)^l (1 + x)^m, l> —1, m > —1. Специальные частные случаи многочленов Якоби соответствуют следующим значениям l и m: l = m— ультрасферические многочлены  (их иногда называют многочленами Гегенбауэра); l = m = —¹/₂, т. е.  —многочлены Чебышева 1-го рода T_n (x); l = m = ¹/₂, т. е.  — многочлены Чебышева 2-го рода U_n (x);

  2) Многочлены Лагерра L_n (x) — при а = 0, b = + ∞ и r(х) = е^—х (их наз. также многочленами Чебышева — Лагерра) и обобщённые многочлены Лагерра  — при .   3) Многочлены Эрмита Н_n (х) — при а = —∞, b = + ∞ и  (их называют также многочленами Чебышева — Эрмита).