13

Интерполяционный многочлен Ньютона.

Определение 1.

Пусть - сетка узлов, - значения функции f(x) в узлах

: значения называются разделенными разностями нулевого порядка функции f(x).

: значения называются разделенными разностями первого порядка функции f(x).

: значения называются разделенными разностями второго порядка функции f(x).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

: значения называются разделенными разностями n–го порядка функции f(x).

Простейшие свойства разделенных разностей.

1. f(x₀, x₁, …, x_k) – симметричная функция своих аргументов, т.е. не меняется при любой перестановке аргументов.

Заметим, что любая разделенная разность есть линейная функция своих аргуметов.

f(x₀, x₁, …, x_k) = .

(устанавливается по индукции) => результат.

Пример:

Установить вид коэффициентов С_j при фиксированном k.

Самостоятельно.

2. Если f(x)=P_n(x) – многочлен n-ой степени, то разделенные разности порядков  (n+1) равны нулю.

Заметим, что P_n(x, x₀) многочлен (n-1)-ой степени,

P_n(x, x₀, x₁) многочлен (n-2)-ой степени,

………………………………………………

P_n(x, x₀, x₁, …, x _n-1) - многочлен 0-ой степени (т.е. const),

P_n(x, x₀, x₁, …, x _n)  0.

………………………………………………

Рассмотрим многочлен n-ой степени вида

(9)

Теорема 3.

Многочлен (9) является интерполяционным для f(x) на сетке узлов , т.е.

, i=0, 1,…, n (10)

Рассмотрим разделенные разности многочлена Лагранжа :

. (11)

Числитель в (11) – многочлен n -ой степени, обращающийся в 0 в т. . Следовательно, по теореме Безу числитель в (11) делится без остатка на , а, следовательно, -многочлен (n-1) -ой степени.

Из (11) находим

. (12)

Далее

. (13)

Числитель в (13) – многочлен степени (n-1) обращается в 0 при ,следовательно, делится на без остатка,  L_n (x, x₀, x₁) - многочлен (n-2)-ой степени.

Из (12) с учетом (13) находим

. (14)

Продолжая таким же образом далее и учитывая, что (n+1) - ая разделенная разность

L_n(x, x₀, …, x_n)  0, окончательно находим

(15)

Но по условию теоремы - интерполяционный многочлен для f(x) , т.е.

, i=0, 1,…, n

Следовательно, все разделенные разности для и f(x) совпадают, поэтому (15) можно переписать

(16)

т.е. получаем представление (9), что и требовалось доказать.

Замечание 1.

Мы получили другую форму представления интерполяционного многочлена Лагранжа. Многочлен (9) называется интерполяционным многочленом Ньютона и обозначается также - .

Замечание 2.

Интерполяционный многочлен в форме Лагранжа содержит значения в явном виде. Это удобно, когда необходимо построить интерполяционный многочлен на тех же узлах, но для другой функции – g(x). Тогда значения достаточно заменить на .

Многочлен в форме Ньютона содержит неявно (через разделенные разности).

Однако, он удобен, когда для той же функции f(x) необходимо увеличить порядок n. Тогда к исходному многочлену достаточно добавить несколько членов стандартного вида.

Запись интерполяционного многочлена для равноотстоящих узлов.

Пусть , h>0, i=0, …, n

Определение 2.

1. Величина называется конечной разностью первого порядка.

2.

Величина

называется конечной разностью второго порядка.

. . . . . . . . . . . . . . . .

n. Величина называется конечной разностью n-го порядка.

Лемма 1.

Для равноотстоящих узлов между разделенными и конечными разностями существует следующая связь:

, k = 0, 1, … (17)

По индукции:

k=0 – очевидно;

k=1

- верно.

Пусть (17) установлено для номера k. Докажем, что тогда оно верно и для номера (k+1).

(k+1):

Т.о., установлено, что (17) верно для k{0, 1, …,n}.

Лемма 2.

Пусть задана сетка равноотстоящих узлов на отрезке [a,b]:

a  x₀ < x₁ <…< x_n < x_n+1  b, x_k = x₀ + hk, k = 0, 1, …, n+1

и .

Тогда существует точка такая, что

(18)

По индукции:

k=1:

k=2:

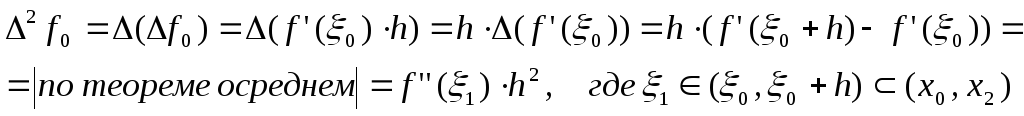
………………………………… и т.д.

k=n+1:

.

Установим теперь вид многочлена Ньютона для равноотстоящих узлов.

Введем переменную . Очевидно, что , если

x-x_k=h(q-k), k = 0, 1, …, n.

В формуле полинома Ньютона (9) выразим все разности (x-x_k) через q и все разделенные разности по формуле (17):

(19)

Оценим погрешность формулы Ньютона (19).

Из формул остаточного члена (4) и (5) с учетом леммы 2, следует

, , и так далее.

Земечание.

Интерполяционную формулу (19) применяют на практике для точек x, близких к x₀. Если необходимо вычислить приближенное значение функции f(x) в точках x, близких к правому концу отрезка, то полагают и записывают интерполяционный многочлен Ньютона в терминах данного q.