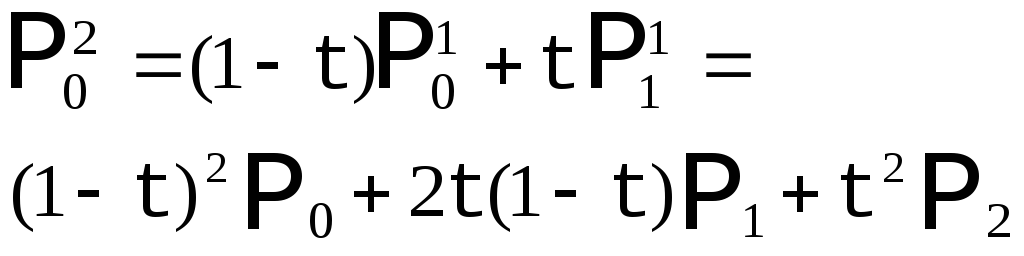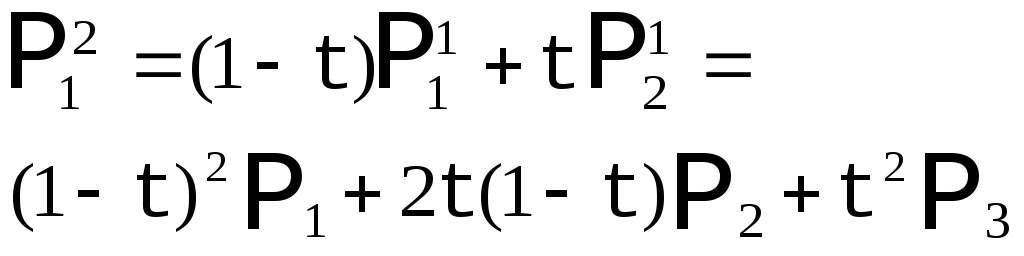6497 / 7. Приближение сплайнами и функциями Бернштейна-Безье
.docИнтерполяция.
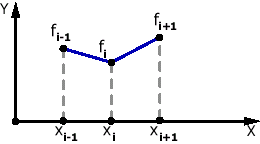
Напомним постановку задачи.
|
Рис. 1. Постановка задачи. |
Дано:
|
-
Ее решением будет, в частности, интерполяционный многочлен Лагранжа
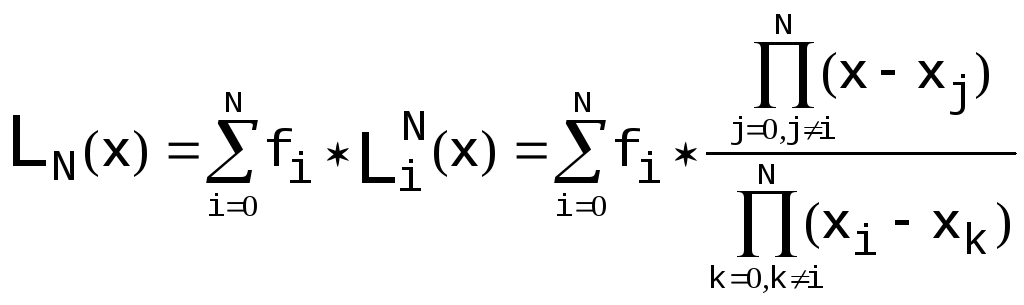 ;
;
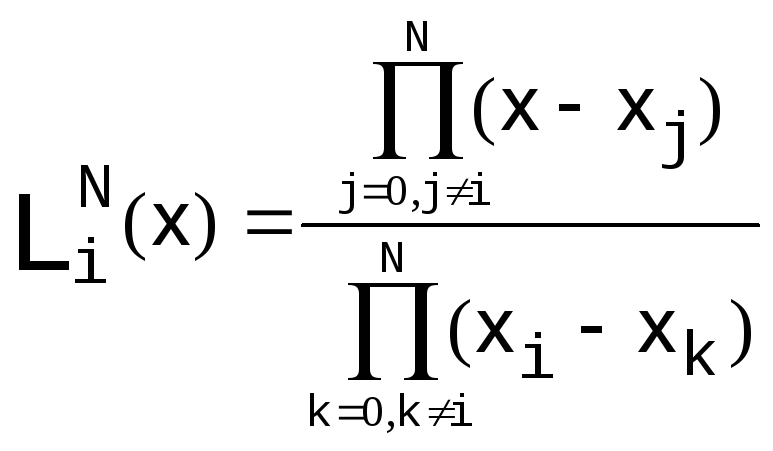 ;
;
![]()
Получаем непрерывную функцию (многочлен степени не выше N), проходящую через все точки.
Минусы:
-
Требует значительного объема вычислений для нахождения значения функции в произвольной точке.
-
Неопределенное поведение построенной функции между узлами, в частности можно привести следующие результаты:
1916г. Бернштейн :
![]()
![]()
![]()
1925г. Рунге :
![]()
![]()
![]()
Далее будем рассматривать интерполирующие
функции, которые задаются отдельно на
каждом отрезке
![]() ,
что позволяет лучше учитывать локальное
поведение требуемой функции и избежать
громоздких вычислений (так как на каждом
из отрезков интерполирующая функция
имеет по возможности простой вид).
,
что позволяет лучше учитывать локальное
поведение требуемой функции и избежать
громоздких вычислений (так как на каждом
из отрезков интерполирующая функция
имеет по возможности простой вид).
2) Кусочно-линейная интерполяция
|
Рис. 2. Кусочно-линейная интерполяция. |
Класс
|
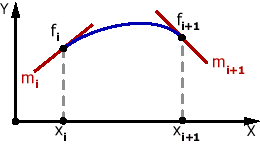
3) Кубическая интерполяция Эрмита
|
Рис. 3. Кубическая интерполяция Эрмита. |
тогда для каждого i будем
искать искомую функцию в виде Класс
|
Проблемы:
-
Непонятно откуда брать значения производных.
-
Хотелось бы
 ,
а не только
,
а не только

4) Сплайны
Сплайн - кусочный полином степени K с непрерывной производной порядка K-1 в точках соединения сегментов.
Далее нас будут интересовать кубические сплайны.
Понятие сплайна пришло из машиностроения,
где сплайном называли гибкую линейку,
закрепив которую в нужных местах,
добивались плавной кривой, которую
затем чертили по этой линейке (см. Рис. 4)
Форма такой линейки, если ее рассматривать
как функцию y(x),
будет удовлетворять уравнению
Эйлера-Бернулли:
![]() ,где
M(x)
- момент изгиба вдоль рейки, E
- модуль Юнга. зависящий от свойств
материала рейки, I
- момент инерции, определяемый формой
кривой. Если мы фиксируем некоторые
точки подпорками, то момент изгиба на
каждом отрезке
,где
M(x)
- момент изгиба вдоль рейки, E
- модуль Юнга. зависящий от свойств
материала рейки, I
- момент инерции, определяемый формой
кривой. Если мы фиксируем некоторые
точки подпорками, то момент изгиба на
каждом отрезке
![]() меняется по линейному закону: M(x)
= A*x
+ B
, подставляя в исходное уравнение
получаем:
меняется по линейному закону: M(x)
= A*x
+ B
, подставляя в исходное уравнение
получаем:
![]() ,
дважды интегрируя получаем уравнение
кривой на данном
,
дважды интегрируя получаем уравнение
кривой на данном
|
Рис. 4. Сплайн. |
отрезке:
Теперь рассмотрим задачу построения
системы таких кубических полиномов
для всего отрезка
|
-
Для N отрезков имеем 4N коэффициентов:
 для
для
 ;
; -
Условия
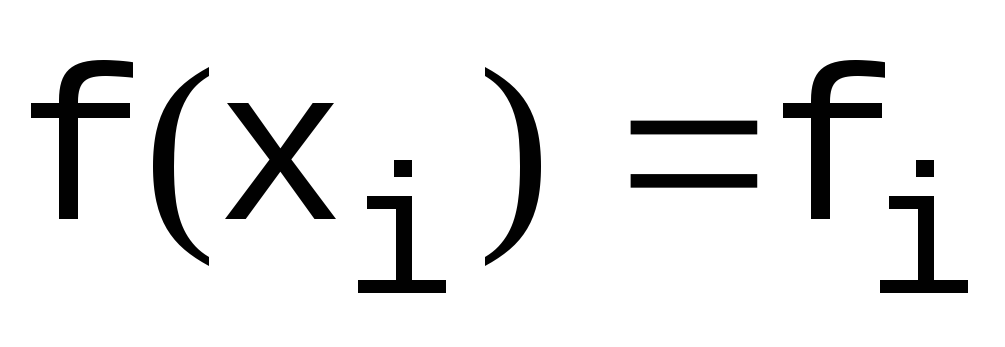 (
i
(
i
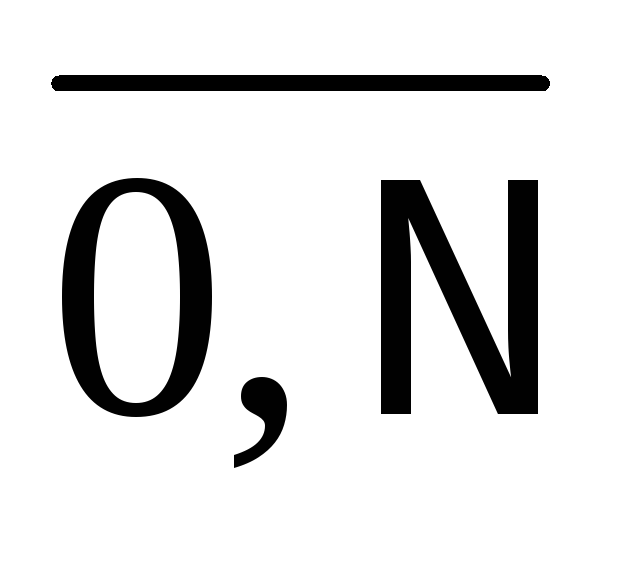 )
дают 2N уравнений;
)
дают 2N уравнений; -
Требование
 в точках
в точках
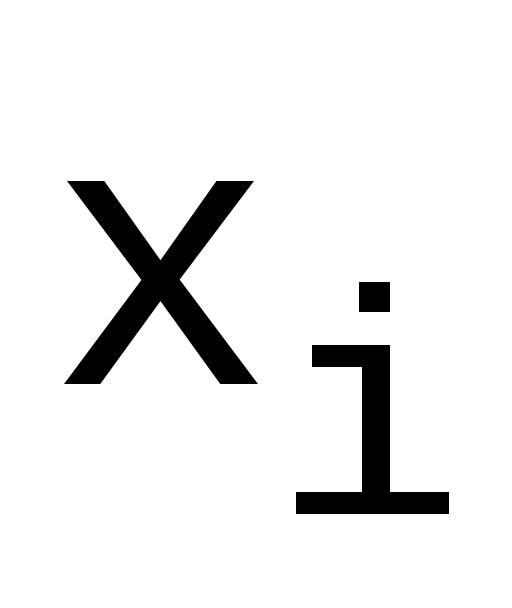 (
i
(
i
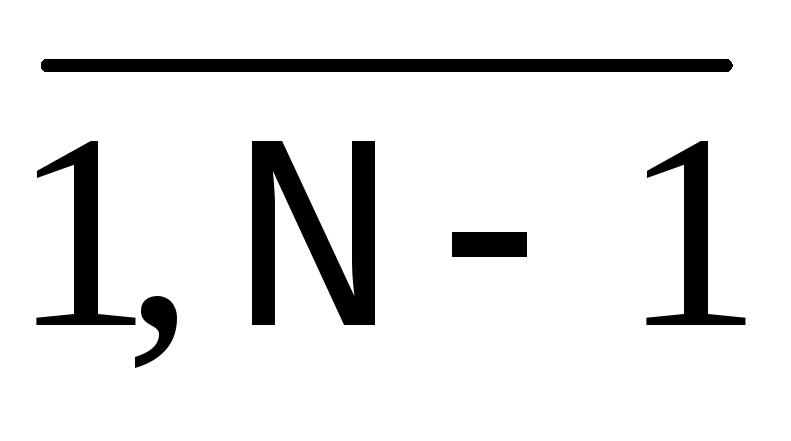 )
дает N-1 уравнений;
)
дает N-1 уравнений; -
Требование
 в точках
в точках
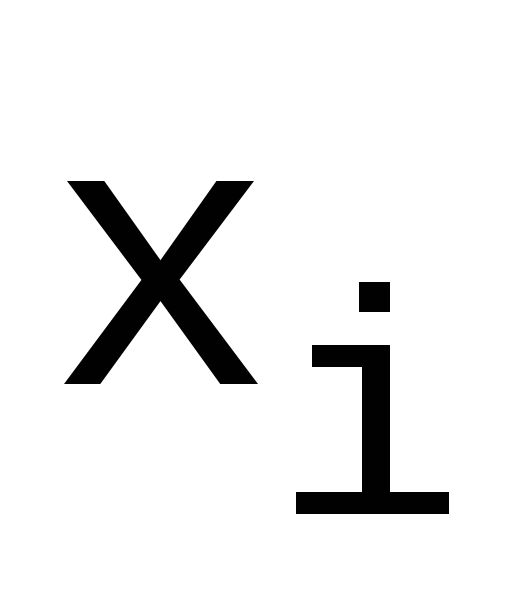 (
i
(
i
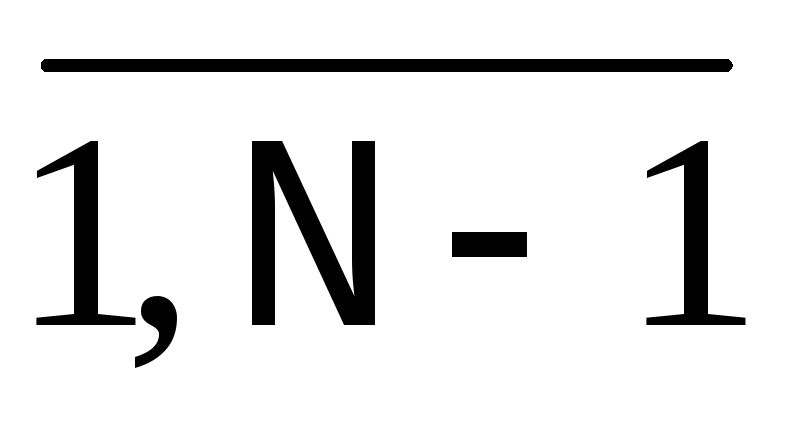 )
дает N-1 уравнений.
)
дает N-1 уравнений.
Итого имеем 4N-2 уравнения;
для того чтобы система была определенной,
необходимы еще 2 уравнения; их можно
вывести, например, из заданных значений
производных на границах или или из
условия периодичности. При корректно
заданных условиях линейная относительно
![]() система имеет единственное решение.
система имеет единственное решение.
Аппроксимация.
1) Кривые Безье
В настоящее время для задач аппроксимации наиболее широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно, т.е. двигая опорные точки курсором на экране ).
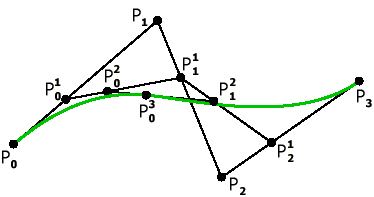
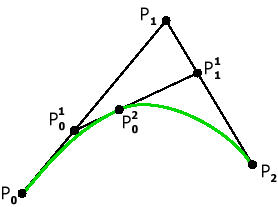
Наглядный метод построения этих кривых был предложен de Casteljau в 1959 году. Построим кривую по 3 опорным точкам (Рис. 5). Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.
|
Рис. 5. Кривая Безье с 3 опорными точками. |
Обозначим опорные точки как
таким образом, получим кривую второго порядка. |
Теперь постоим аналогичным методом кривую Безье с 4 опорными точками.
|
Рис. 6. Кривая Безье с 4 опорными точками. |
|
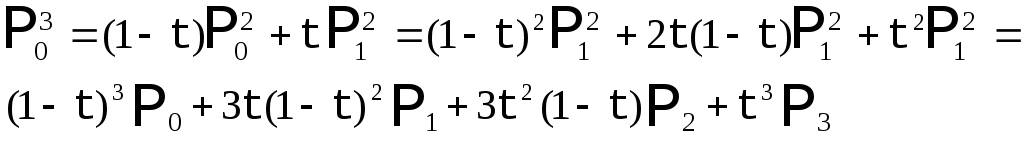
Можно продолжать подобные построения и для большего числа узлов, получая аналогичные выкладки. Запишем общее аналитическое представление для кривой Безье с N+1 опорной точкой:
![]() ,
где
,
где
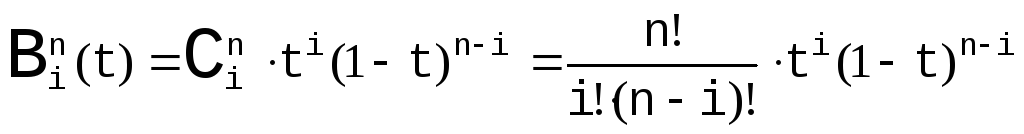 ,
где
,
где
![]() - биномиальные коэффициенты,
- биномиальные коэффициенты,
![]() называются базисными многочленами
Бернштейна n степени
(а также весовыми функциями Безье/Бернштейна).
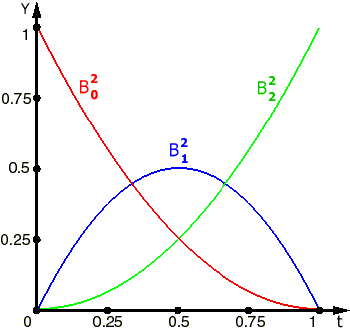
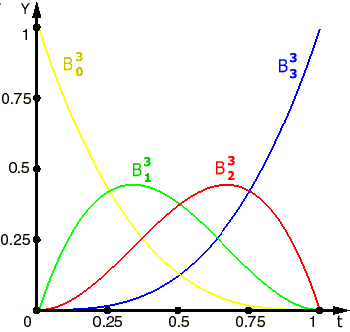
На рисунках ниже изображены многочлены
Бернштейна 3 и 4 степеней
называются базисными многочленами
Бернштейна n степени
(а также весовыми функциями Безье/Бернштейна).
На рисунках ниже изображены многочлены
Бернштейна 3 и 4 степеней
![]()
![]()
|
Рис. 7. Базисные функции Бернштейна для кривой Безье с 3 опорными точками. |
|
|
Рис. 8. . Базисные функции Бернштейна для кривой Безье с 4 опорными точками. |
|
Свойства кривых Безье
1) Инвариантность относительно аффинных преобразований;
2) Инвариантность относительно линейных замен параметризации;
-
Кривая Безье принадлежит выпуклой оболочке опорных точек (следует из геометрического способа построения);
Следствие: Если все опорные точки лежат на одной прямой, то кривая Безье вырождается в отрезок, соединяющий эти точки.
4) Кривая Безье проходит через
![]() и
и
![]() ;
;
5) Симметричность: если рассматривать контрольные точки в противоположном порядке, то кривая не измениться;
6) Степень многочлена, представляющего кривую в аналитическом виде на 1 меньше числа опорных точек;
7) Векторы касательных в точках
![]() и
и
![]() коллинеарны
коллинеарны
![]() и
и
![]() ,соответственно.
,соответственно.
Замечание:
Хотя все выкладки проводились в
![]() ,
аналогичные построения и свойства
справедливы и в
,
аналогичные построения и свойства
справедливы и в
![]() .
.

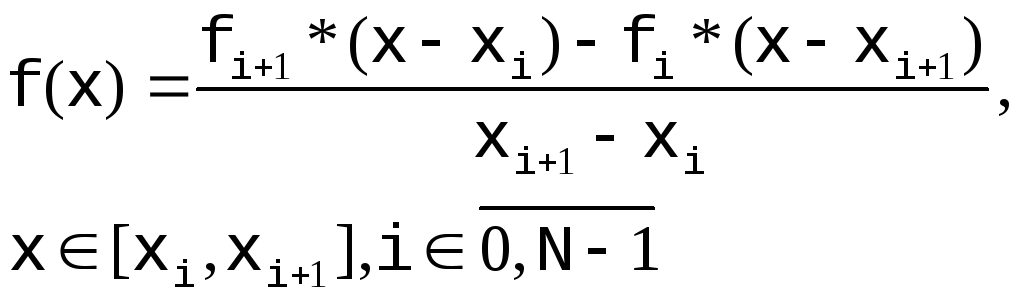
 ,
,
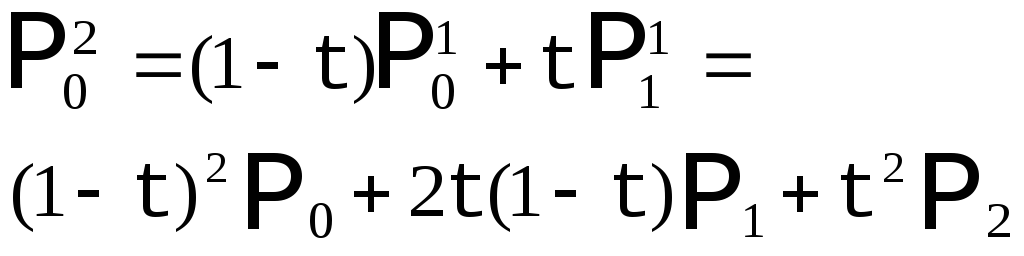 ,
,