6497 / 4. Теорема Бореля, альтернанс

28

Теоремы о равномерном приближении функций на отрезке.

Рассмотрим более подробно задачу второго типа:

, ,

многочлен n-ой степени,

найденный многочлен наилучшего равномерного приближения.

Сложность в том, что данное нормированное пространство C[a,b] не является гильбертовым, т.к. в нем не определено скалярное произведение (хотя оно ‑ полное, нормированноебанахово).

Поэтому не работают те теоремы существования и единственности, которые естественным образом доказываются в гильбертовом пространстве (например, в ). Эти теоремы необходимо передоказать.

Теорема 1 (Э.Борель).

Пусть линейно независимая при система непрерывных на [a,b] функций;

“обобщённый” полином n-ой степени по данной системе.

такой набор коэффициентов что многочлен является наилучшим равномерным приближением функции f(x) на [a,b].

Обозначим

.

В силу свойств нормы функция - непрерывная функция своих аргументов.

Действительно, согласно неравенству треугольника для нормы

Оценивая обе части неравенства по модулю, получаем:

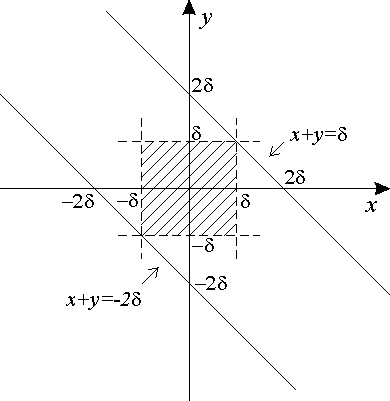
Положим

Последнее неравенство и доказывает непрерывность функции (с₀,…, с_n) при fC[a,b].

Запишем тождественно:

(1)

Если , то из (1) . Поэтому для поиска минимального элемента достаточно рассматривать лишь такие , которые удовлетворяют условию

, или . (2)

Используем неравенство Коши-Буняковского:

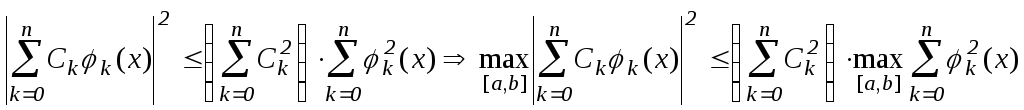. (3)

В силу непрерывности на [a,b], существует

.

Подставляя (3) в (2)

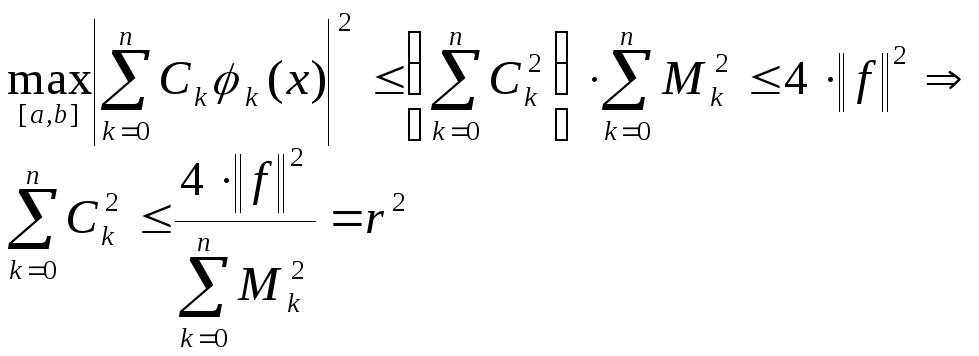(4)

Неравенство (4) определяет так называемый замкнутый шар в пространстве коэффициентов .Так как непрерывна в замкнутом шаре по теореме Вейерштрасса достигает своего минимального значения набор , такой что наилучшее равномерное приближение для f(x).

В дальнейшем более подробно будем рассматривать случай

.

т.е. будем искать равномерное приближение непрерывной функции f(x) на [a,b] алгебраическим многочленом n-ой степени.

Сформулируем основную Теорему Чебышева – критерий наилучшего равномерного приближения.

Теорема 2.(Чебышева).

Чтобы многочлен был многочленом наилучшего равномерного приближения непрерывной на [a,b] функции f(x) необходимо и достаточно существование на [a,b] по крайней мере (n+2)- точек , таких что

, (5)

,

одновременно для всех i.

Другими словами: равенство (5) устанавливает следующее свойство разности в указанных точках:

1)меняет знак последовательно в каждой точке {},

2)принимает одно и то же максимальное по модулю значение, равное

.

Без доказательства

Определение.

Точки , удовлетворяющие условию теоремы называются точками Чебышевского альтернанса.

Определение.

Многочлен , решающий задачу наилучшего равномерного приближения называется наилучшим T-приближением для f(x) на [a,b].(от немецкой транскрипции фамилии Чебышева: Tchebyscheff).

Теорема 3.

Многочлен , являющийся наилучшим Т-приближением –единственен.

От противного.

Обозначим

.

Пусть существуют два многочлена наилучшего Т-приближения и , :

Рассмотрим норму разности:

многочлен имеет ту же степень n и является наилучшим T-приближением.

Пусть - точки Чебышевского альтернанса для этого многочлена

,

или, запишем иначе:

. (6)

Но так как и - два наилучших Т-приближения

и , (7)

так как -максимально возможное отклонение для и . Из (6) и (7)

, т.е. многочлены и - совпадают в (n+2)-х точках, что невозможно, поскольку они n-ой степени и по предположению не совпадают тождественно. Полученное противоречие доказывает теорему.

Пояснение.

Условия (6) и (7) запишем в абстрактной форме:

графически только две точки пересечения

Теорема 4.

Пусть , причем на [a,b] ровно (n+2) экстремальные точки для разности , где - наилучшее Т-приближение для f(x), причем концевые точки отрезка a и b – принадлежат к числу точек альтернанса.

Обозначим .

По теореме об альтернансе по крайней мере (n+2) точки , в которых меняет знак и достигает своего максимального по модулю значения .

Пусть этих точек будет больше чем (n+2).Найдется такая константа C, что разность обратится в нуль, по крайней мере, в (n+2) точках. Отсюда по теореме Ролля обратилась бы в нуль, по крайней мере, в одной точке, что противоречит условию теоремы.

Получено противоречие с утверждением, что точек альтернанса больше, чем (n+2).

Предположим, что концевые точки отрезка a и b - не являются точками альтернанса, следовательно, как и в предыдущем случае найдется такая константа C, что уравнение будет иметь (n+2) корня тот же вывод, что и выше противоречиерезультат

Графическая иллюстрация.

Изобразим график для случая n=2. Пусть концы отрезка a и b не входят в число точек альтернанса.

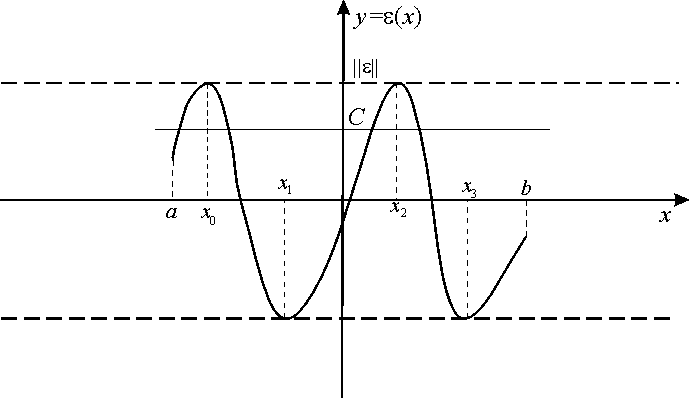
Из рисунка видно, что нашлась такая константа С, что прямая y=C пересекает график в 4-х точках. Отсюда по теореме Ролля   точка (a,b): f⁽³⁾()=0.

Пример 1.

. Найти наилучшее Т-приближение, многочленом нулевой степени.

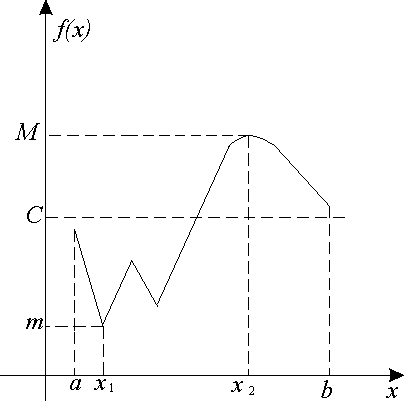
n=0, . Заметим, что достаточные условия, сформулированные в теореме 4, могут не выполнятся, например, для функции, изображенной на рисунке:

В точке - точка локального экстремума, тем не менее, достаточно иметь ровно 2 точки альтернанса.

Пусть

и - точки чебышевского альтернанса

- легко проверить выполнение условий теоремы 2

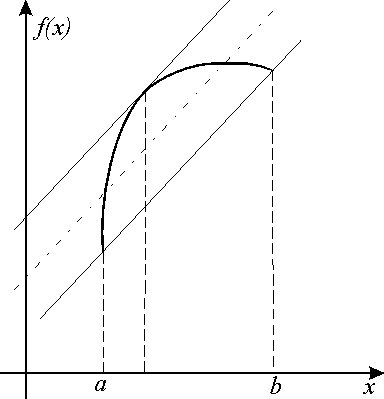
Пример 2.

и строго выпукла вверх. Найти наилучшее Т-приближение многочленом 1-го порядка.

n=1,.

Применим геометрический метод решения.

Так как условия теоремы 4 выполнены, то и остается найти одну точку . Искомая точка -точка, в которой касательная к графику y=f(x) параллельна хорде, соединяющей точки (a,f(a)) и (b,f(b)) искомая прямая проходит посередине между касательной и хордой.