3. Методы поиска решений на моделях

   1. Методы поиска оптимальных решений для однокритериальных моделей с детерминированными факторами

Аналитические исследования

При аналитическом исследовании моделей математического программирования используются общеизвестные методы отыскания экстремальных значений – классические методы оптимизации. В качестве основного математического аппарата применяется дифференциальное исчисление для нахождения значения переменных, максимизирующих или минимизирующих целевую функцию. Для использования этих методов математическую модель необходимо преобразовать в систему уравнений относительно искомых величин. Результатом решения аналитической модели является либо получение формул для вычисления искомых величин, либо приведение уравнений к виду, для которого решения известны. При моделировании сложных процессов осуществление таких преобразований является достаточно сложной задачей.

В классических задачах оптимизации целевая функция и уравнение связидолжны быть по крайней мере дважды дифференцируемыми функциями, а ограничения – иметь вид строгих равенств.

Классические задачи оптимизации разделяются на два подкласса:

1. Задач а отыскания безусловного экстремума. В этих задачах отсутствуют ограничения на область допустимых значений переменных управления 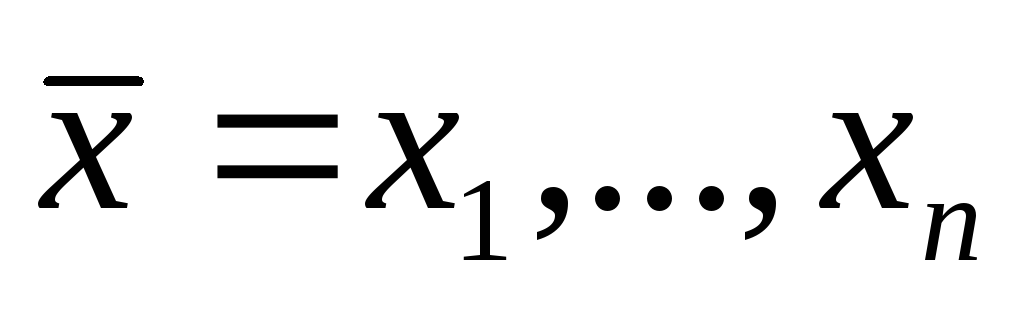, т.е. отсутствует функция. Постановка задачи имеет вид

. (3.1)

2. Задачи отыскания условного экстремума с ограничениями типа равенств. Постановка задачи имеет вид

;

. (3.3)

где – векторы констант модели.

Задача типа (3.2) в результате применения метода множителей Лагранжа сводится к задаче (3.1). При этом исходная функция заменяется функцией Лагранжа

, (3.3)

где - неопределенные коэффициенты.

Классический подход к решению задачи безусловной оптимизации состоит в использовании необходимого условия экстремума функции. Необходимым (но не достаточным) условием существования экстремума непрерывной функции является равенство нулю всех ее частных первых производных, т.е. условия , либо для (3.3)

; (3.4)

. (3.5)

Корни систем уравнений (3.4), (3.5) называются стационарными. Эти точки «подозрительны» на предмет нахождения в них максимума, минимума или седловых точек функций , либо.

Процедура решения задачи оптимизации классическим методом состоит из следующих этапов:

• получение и решение системы уравнений (3.4) или (3.5) с целью определения всех стационарных точек;

• анализ тем или иным способом стационарных точек для выявления всех максимумов (минимумов) Функции;

• сравнение между собой максимальных (минимальных) значений функций ,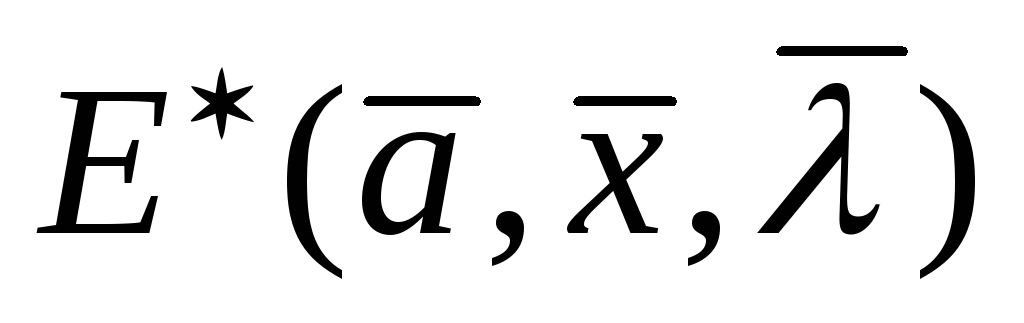с целью определения глобального максимума (минимума).

Получаемые в процессе решения системы уравнений (3.5) значения коэффициентов характеризует влияние ограничений на нахождение оптимальных значений. При, близком к нулю,j-е ограничение несущественно влияет на нахождение оптимума. Информация о значениях коэффициентов, полученная в результате расчета, дает возможность проверить правильность формирования концептуальной модели, например, сопоставить приоритетность ограничений концептуальной модели с приоритетностью, получаемой в результате расчета. Это может привести к пересмотру концептуальной модели, исключению одних и включению других (новых) ограничений.

Зачастую аналитическое решение систем уравнений удается получить в виде параметрических формул

,

что позволяет определить влияние изменения различного рода факторов модели на оптимальность решения, в том числе оценивать чувствительность полученного решения к действию случайных и неопределенных факторов.

Несмотря на принципиальную ясность в отношении классических методов решения задач безусловной оптимизации, на этом пути могут встретиться вычислительные трудности, которые делают необходимым поиск соответствующих методов решения. Так, только для систем линейных уравнений любого порядка разработаны точные методы нахождения решения, например методы Крамера, Гаусса и др. В общем же в случае уравнения типа (3.4), (3.5) являются нелинейными. Для отыскания точного решения произвольной системы уравнений высокого порядка не существует какой-либо надежной вычислительной схемы. Для определения приближенного решения может быть использован метод Ньютона и его модификации.

Введение ограничений типа неравенства и ограничений на положительность переменных, что принципиально важно для экономических исследований, приводит к необходимости поиска решений подобных аналитических моделей методом Куна-Таккера, являющимся одной из разновидностей численных методов.

Исследование модели при помощи численных методов

Более широкую сферу применения имеет исследование процессов при помощи численных методов. Численные методы – это итерационные вычислительные процессы для определения экстремальных состояний модели.

С вычислительной точки зрения процесса поиска оптимальных решений с помощью численных методов состоит из следующих многократно повторяющихся этапов:

1.Выбор начального значения переменных, удовлетворяющих уравнениям связи математической модели, и расчет соответствующего им значения целевой функции.

2. выбор направления и шага изменения переменных.

3.Определение нового значения переменных, соответствующих уравнениям связи, и расчет нового значения целевой функции.

4. Сравнение предыдущего и последующего значений целевой функции, переход к п.2 либо останов процесса при достижении экстремума.

Если при нахождении максимального (минимального) значения целевой функции последующее значение меньше (больше) предыдущего, то направление корректировки управляемых переменных меняется. Если по любому направлению происходит ухудшение целевой функции, то считается, что оптимальные значения переменных найдены.

Численные методы отличаются друг от друга в основном принципами выбора начального значения переменных, направления и шага их изменения.

Решение задачи с помощью численных методов является обычно менее полным и точным по сравнению с аналитическим исследованием, но класс моделей, которые могут быть решены приближенно численными методами, значительно шире, чем класс моделей, доступных аналитическому исследованию. Однако если в аналитическом методе находится за один просчет точное решение, то в численном методе в общем случае за n просчетов (итераций) находится приближенное решение.

Выбор наиболее эффективного с вычислительной точки зрения численного метода зависит от конкретного вида математической модели. В практике экономических исследований широко используются модели линейного, кусочно- и дробно-литейного, целочисленного, нелинейного (в том числе и выпуклого), динамического программирования.

В литературе по математическому программированию дается описание широкого круга задач математического программирования и методов решения.

Для значительного числа моделей математического программирования разработаны эффективные алгоритмы и программы поиска экстремума, включенные в Общегосударственный фонд алгоритмов и программ. Ряд наиболее применяемых численных методов оформлен в виде стандартных программ математического обеспечения современных ЭВМ, наличие которых позволяет исследователю миновать этапы алгоритмизации, программирования и отладки программы на ЭВМ, что существенно сокращает время получения результата. После отнесения математической модели к тому или иному классу разработчик должен выбрать соответствующий этому классу вычислительный метод (алгоритм, программу на ЭВМ) поиска оптимального решения.

Экспериментальная оптимизация на ЭВМ

Если математическая модель непригодна для применения аналитических или численных методов, а это присуще всем моделям алгоритмического вида, то для ее решения применяют метод экспериментальной оптимизации ЭВМ. При этом методе не обязательно преобразовывать математическую модель в специальную систему уравнений. При этом методе не обязательно преобразовывать математическую модель в специальную систему уравнений.

Как целевая функция, так и система ограничений могут быть заданы в виде алгоритма, позволяющего вычислить их значения в ходе моделирования. Как уже указывалось выше, характерным примером алгоритмических моделей являются имитационные модели, реализуемые на ЭВМ в виде моделирующего алгоритма.

В процессе реализации данного метода, так же как и для любого численного метода, выполняются перечисленные выше этапы: выбор начальных значений переменных, расчет значения целевой функции, определение направления и шага изменения переменных и т.д., в связи с чем он является численным методом, имеющим своеобразные отличия.

Каждый численный метод нахождения оптимальных решений в задачах математического программирования ориентирован на какой-то класс математических уравнений, для которого он является либо единственным методом решения, либо наиболее эффективным. В рамках данного метода обоснованы и выбор начальных значений переменных, и вопросы анализа получения результатов с целью определения направления и шага их изменения.

Алгоритмические модели в силу специфичности их математической записи не позволяют в ряде случаев даже качественно определить вид целевой функции (например, мономодальная или полимодальная). В связи с этим перед исследователем помимо создания моделирующего алгоритма возникают проблемы разработки алгоритма оптимизации, включающего моделирующий алгоритм в качестве одного из элементов – этапа расчета значения целевой функции для определенных значений переменных. Для этого им должна бать продумана алгоритмическая и программная реализация всех вышеназванных этапов.

Существуют два метода экспериментального поиска оптимальных решений: параллельный и последовательный. При использовании параллельного метода все комбинации значений переменных, при которых должны рассчитываться значения целевой функции, выбираются заранее, в то время как в случае применения последовательного метода заранее определяется несколько начальных значений, а остальные выбираются лишь по мере накопления данных.

Два основных параллельных метода называются методами случайного поиска и многофакторного анализа и основаны на априорном выборе определенных интервалов изменения переменных x₁,x₂,…,x_n. Границы этих интервалов определяются, с одной стороны, из предположения, что внутри них находятся оптимальные значения, а с другой – из условия выполнения ограниченной модели.

В первом методе случайным образом устанавливаются точки эксперимента. В которых значения x₁,x₂,…,x_nпринадлежат этим интервалам, причем выбор значения каждой переменной производится независимо. Для каждой зафиксированной точки рассчитывается значение целевой функции. В качестве решения выбирается такая точка, для которой целевая функция принимает экстремальное значение, либо производится более тщательный поиск экстремума в окрестности этой точки ( обычно методом многофакторного анализа).

При использовании метода многофакторного анализа интервалы изменения каждой из nпеременных разбиваются наmподинтервалов, которые определяют уровни их изменения. Значения переменных для точек эксперимента формируют путем объединения значений по каждому уровню для всех переменных, что дает в результатеNэкспериментов (полный факторный эксперимент):

,

где m_i – число значений (уровней)i = 1, 2,…,n– число переменных модели.

Далее для каждой точки рассчитывается значение целевой функции и либо выбирается наилучшая точка, либо более тщательно (т.е. с меньшей величиной подинтервалов) исследуется окрестность этой точки. Различия между описанными параллельными методами экспериментальной оптимизации показаны на рис.3.1.

Рис. 3.1. Параллельные методы экспериментальной оптимизации на ЭВМ

Последовательные методы экспериментального поиска чаще всего основаны на принципах построения численных методов, описанных выше. В качестве базовых используются симплекс-метод, метод покоординатной оптимизации, градиентный метод и его модификация.

Однако далеко не всегда возможно поведение последовательного экспериментального поиска на принципах численного метода. Трудности строгой математической формализации и разработки методов нахождения оптимальных решений в задачах проектирования сложных систем или процессов и управления ими привели к созданию большого числа так называемых эвристических алгоритмов поиска наилучших решений для решения разнообразных практических задач. Примерами подобных алгоритмов служат многочисленные методы решения задач оперативно-календарного планирования производства, каждый из которых формализует опыт специалистов при формировании планов запуска-выпуска деталей в тех или иных специфических условиях. С содержательной точки зрения эвристические алгоритмы представляют собой набор правил конструирования, сравнения, анализа и отбора вариантов возможных решений. От алгоритмов математическое программирования эти алгоритмы отличаются тем, что они не гарантируют получение оптимального решения – в них производится выбор наилучшего решения из просмотренных.

Качество эвристических алгоритмов зависит от того, насколько тесно связаны правила отбора вариантов, лежащих в основе этих алгоритмов, с «идеальными» правилами отбора, вытекающими из точной постановки задачи. Эвристические алгоритмы обычно применяются для проектирования и управления объектами с большим набором признаков и свойств, для которых, с одной стороны, затруднительно полное математическое описание и применение разработанного математического аппарата, а с другой – возможно построить достаточно простые и гибкие правила отбора вариантов.

При использовании любого метода последовательной экспериментальной оптимизации на ЭВМ все работы по алгоритмизации, программированию и отладке модели приходится выполнять разработчику модели. От правильности выбора исследователем принципов построения алгоритма последовательной экспериментальной оптимизации во многом зависят объемы вычислений при нахождении оптимального решения.