
лекции полностью
.pdfИнформатика |
Пчелинцева Е.Г. |
централизованного накопления и коллективного многоцелевого использования этих данных.
Согласно ст. 1 закона «О правовой охране программ для ЭВМ и баз данных», «база данных - это объективная форма представления и организации совокупности данных, систематизированных таким образом, чтобы эти данные могли быть найдены и обработаны с помощью ЭВМ».
1.5. Количество информации
Количеством информации называют числовую характеристику сигнала, отражающую ту степень неопределенности (неполноту знаний), которая исчезает после получения сообщения в виде данного сигнала. Эту меру неопределенности в теории информации называют энтропией. Если в результате получения сообщения достигается полная ясность в каком-то вопросе, говорят, что была получена полная или исчерпывающая информация и необходимости в получении дополнительной информации нет. И наоборот, если после получения сообщения неопределенность осталась прежней, значит, информации получено не было (нулевая информация).
Приведенные рассуждения показывают, что между понятиями
информация, неопределенность и возможность выбора существует тесная связь. Так, любая неопределенность предполагает возможность выбора, а любая информация, уменьшая неопределенность, уменьшает и возможность выбора. При полной информации выбора нет. Частичная информация уменьшает число вариантов выбора, сокращая тем самым неопределенность.
Возможно ли объективно измерить количество информации?
Важнейшим результатом теории информации является следующий вывод: в определенных, весьма широких пределах можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных.
В настоящее время получили распространение подходы к определению понятия «количество информации», основанные на том, что информацию,
содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте.
Эти подходы используют математические понятия вероятности и логарифма.
Пример. Человек бросает монету и наблюдает, какой стороной она упадет. Обе стороны монеты равноправны, поэтому одинаково вероятно, что выпадет одна или другая сторона. Такой ситуации приписывается начальная неопределенность, характеризуемая двумя возможностями. После того как монета упадет, достигается полная ясность и неопределенность исчезает (становится равной нулю).
Приведенный пример относится к группе событий, применительно к которым может быть поставлен вопрос типа «да-нeт». Количество информации, которое можно получить при ответе на вопрос типа «да-нет»,
Информатика |
Пчелинцева Е.Г. |
называется битом (англ. bit - сокращенное от binary digit - двоичная единица). Бит - минимальная единица количества информации, ибо получить информацию меньшую, чем 1 бит, невозможно. При получении информации в 1 бит неопределенность уменьшается в 2 раза. Таким образом, каждое бросание монеты дает нам информацию в 1 бит.
В качестве других моделей получения такого же количества информации могут выступать электрическая лампочка, двухпозиционный выключатель, магнитный сердечник, диод и т.п. Включенное состояние этих объектов обычно обозначают цифрой 1, а выключенное - цифрой 0.
Рассмотрим систему из двух электрических лампочек, которые независимо друг от друга могут быть включены или выключены. Для такой системы возможны следующие состояния:
лампа А 0 0 1 1 лампа В 0 1 0 1
Чтобы получить полную информацию о состоянии системы, необходимо задать два вопроса типа «да-нет»: по лампочке А и лампочке В соответственно. В этом случае количество информации, содержащейся в данной системе, определяется уже в 2 бита, а число возможных состояний системы - 4. Если взять три лампочки, то необходимо задать уже три вопроса и получить 3 бита информации. Количество состояний такой системы равно
8 и т.д.
Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N.
Формула Хартли: I = log2N.
Ту же формулу можно представить иначе: N= 2i, где i - количество информации в битах; N - число возможных состояний.
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 = 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации.
Приведем другие примеры равновероятных сообщений:
1)при бросании монеты: «выпала решка», «выпал орел»;
2)на странице книги: «количество букв чётное», «количество букв
нечётное».
Определим теперь, являются ли равновероятными сообщения: «первой выйдет из дверей здания женщина» и «первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то
Информатика |
Пчелинцева Е.Г. |
вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
Формула Шеннона: I = - ( p1log2 p1 + p2 log2 p2 + . . . + pN log2 pN),
где pi - вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
Легко заметить, что если вероятности p1, ..., pN равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли.
В качестве единицы информации Клод Шеннон предложил принять один бит.
Бит в теории информации - количество информации, необходимое для различения двух равновероятных сообщений (типа «орел»-«решка», «чет»- «нечет» и т.п.).
В вычислительной технике битом называют наименьшую «порцию» памяти компьютера, необходимую для хранения одного из двух знаков - «0» и «1», используемых для внутримашинного представления данных и команд.
Бит - слишком мелкая единица измерения. На практике чаще применяется более крупная единица - байт, равная восьми битам. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=28).
Широко используются также ещё более крупные производные единицы информации:
1 килобайт (Кбайт) = 1024 байт = 210 байт, 1 мегабайт (Мбайт) = 1024 Кбайт = 220 байт, 1 гигабайт (Гбайт) = 1024 Мбайт = 230 байт. 1 терабайт (Тбайт) = 1024 Гбайт = 240 байт, 1 петабайт (Пбайт) = 1024 Тбайт = 250 байт.
При хранении и передаче информации с помощью технических средств целесообразно отвлечься от содержания информации и рассматривать ее как последовательность знаков. Набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния. Если считать, что появление символов в сообщении равновероятно, то по формуле m=2n, где m - общее количество символов алфавита, а n – количество информации, которую несет каждый символ, можно рассчитать, какое количество информации несет каждый символ, или, другими словами, сколько двоичных ячеек памяти потребуется для хранения каждого символа.
Например, в русском алфавите, если не считать букву ё, количество букв равно 32. Тогда 32=2n, откуда n=5 битов. Поэтому каждый символ несет 5 битов информации, а количество информации в сообщении можно подсчитать, умножив количество информации, которое несет один символ,
Информатика |
Пчелинцева Е.Г. |
на количество символов. Такой подход к измерению количества информации называют синтаксическим.
Для человека же существенное значение имеют именно смысл передаваемого сообщения и получаемые при этом знания, т.е. на основе смысловой информации вырабатывается и закрепляется соответствие между будущими символами или образами на входе и необходимыми действиями. Высшие животные не могли бы существовать, если бы у них не было достаточного соответствия (как бы смыслового словаря) между разнообразными сигналами ситуаций внешней среды (запах хищника, запах добычи и т.д.) и целесообразными в этих ситуациях действиями. У человека смысловая информация идет на пополнение соответствий не только между внешними сигналами и действиями, но и между понятиями. Следовательно, общей чертой смысловой информации является то, что она изменяет запас сведений, запас соответствий у получателя информации. Первоначальный (и меняющийся в ходе поступления информации) запас соответствий можно представить себе как некоторый обобщенный словарь или справочник, который Ю.А.Шрейдер предложил называть тезаурусом (греч. «тезаурус» – сокровище; имеются в виду словари, где даны не только значения слов, но и связи между ними). В качестве меры количества смысловой информации естественно взять изменение тезауруса приёмника под действием поступившей информации.
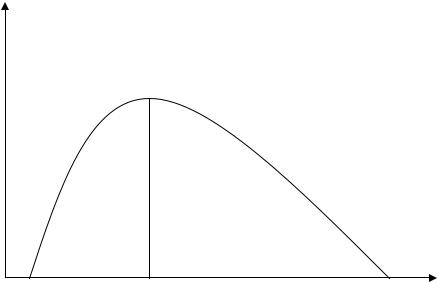
Таким образом, тезаурусная (семантическая) мера связывает смысловые свойства информации со способностью пользователя понимать поступившее сообщение. Количество информации (Ic) в этом случае зависит от смыслового содержания сообщения (S) и тезауруса приёмника (Sp). Характер такой зависимости показан на рис 3.
Ic
Sp opt |
|
Sp |
|
|
|
Рисунок 3. График изменения семантической меры информации
Рассмотрим два предельных случая, когда количество семантической информации (Ic) равно 0. Если тезаурус приёмника слишком беден (Sp=0), количество информации в сообщении равно нулю, так как пользователь не
Информатика |
Пчелинцева Е.Г. |
понимает поступающие сведения. Например, в сообщении «Это учебник по высшей математике для 1 курса» трехлетний ребенок совсем ничего не поймет, а школьник старших классов уже кое-что выделит. Максимальную информацию, очевидно, извлечет студент того курса, для которого этот учебник предназначен. Любопытно, что по мере дальнейшего расширения тезауруса приёмника воспринимаемая информация начинает уменьшаться. Уже у студента второго курса при чтении учебника для 1 курса изменение тезауруса будет меньше, а для человека, хорошо знающего высшую математику (Sp → ), этот учебник не несет никакой информации.
Таким образом, максимальное количество информации приёмник получает при согласовании ее смыслового содержания со своим тезаурусом Sp (Sp = Sp opt), когда поступающие сведения понятны и несут ранее не известные сведения. Количество семантической информации является величиной относительной и зависит от компетентности получателя (пользователя).
Прагматическая мера информации определяет полезность, ценность информации для достижения поставленной цели. В этом случае оценка количества информации основывается на законах теории вероятностей, точнее, определяется через вероятности событий (формула Шеннона). Это и понятно. Сообщение имеет ценность, несет информацию только тогда, когда мы узнаем из него об исходе события, имеющего случайный характер, когда оно в какой-то мере неожиданно.
Вэкономических системах ценность информации измеряют в тех же единицах, что и целевую функцию системы: прибыль, время обработки и принятия решения и т.п.
Всистемах автоматизированной обработки данных для измерения объемов информации используется синтаксическая мера (байт и его производные). Это объясняется тем, что эти системы организуются в виде хранилищ данных – баз данных, доступ к которым имеют разные пользователи для решения большого спектра задач.
Мы уже говорили, что понятие информации неразрывно с процессом информирования, который предполагает наличие трех компонентов: источник, получатель и канал передачи информации.
Различные количества информации передаются по каналам связи. Количество проходящей через канал информации не может быть больше его пропускной способности, которая определяется количеством информации проходящей через канал за единицу времени.
Основная масса информации собирается, передается и обрабатывается с помощью знаков. Знаки - это сигналы, которые могут передавать информацию при наличии соглашения об их смысловом содержании между источниками и приемниками информации. Набор знаков, для которых существует указанное соглашение, называется знаковой системой или
языком.
Информатика |
Пчелинцева Е.Г. |
Информацию «просеивают» самым тщательным |
образом. В телеграфе |
часто встречающиеся буквы, сочетания букв, даже целые фразы изображают более коротким набором нулей и единиц, а те, что встречаются реже, более длинным. В случае, когда уменьшают длину кодового слова для часто встречающихся символов и увеличивают для редко встречающихся, говорят об э ф ф е к т и в н о м к о д и р о в а н и и информации.
1.6.Язык, коды, кодирование
Любое сообщение пишется на каком-либо языке. Язык – это форма (способ) общения, форма хранения и передачи знаний, а также средство получения новых знаний, непосредственно связанное с мышлением.
В информатике и информационных технологиях под языком понимают совокупность символов, соглашений, правил, используемых для отображения и передачи информации, средство описания данных и алгоритмов решения задач.
Упорядоченная последовательность символов – это алфавит языка.
Пусть А={а1, а2, …, аn} – алфавит некоторого языка. А* - множество всевозможных последовательностей символов этого языка.
Язык – это подмножество А*, которое удовлетворяет двум системам правил: синтаксическим и семантическим, причем семантическим правилам могут удовлетворять только те конструкции, которые удовлетворяют синтаксическим правилам.
Пример: 1) «ббсе» – не удовлетворяет синтаксису русского языка;
2) «Петя съел трактор» – все синтаксические правила соблюдены, но предложение не удовлетворяет семантике русского языка.
Таким образом, знание языка означает:
1.Знание его алфавита;
2.Знание синтаксических правил;
3.Знание семантических правил.
Вэтом случае вы сможете общаться и будете правильно поняты.
Преобразование конструкций одного языка в последовательность букв другого алфавита называется кодированием.
Если говорить о кодировании, то сначала надо определить, какую конструкцию языка будем рассматривать в качестве символа, т.е. некоторой неделимой конструкции.
Рассмотрим некоторое предложение языка Q. Предложение состоит из слов, которые в свою очередь состоят из букв. Возможны три варианта определения символа (неделимой конструкции языка):
Информатика |
Пчелинцева Е.Г. |
1.Символ = буква. Такой подход используется при письменной
записи;
2.Символ = слово. Такое представление предложений используется
встенографии;
3.Символ = предложение. Такая ситуация возникает при переводе с одного языка на другой, причем особенно ярко это проявляется при переводе пословиц, шуток, поговорок.
Проблемой кодирования начал заниматься великий немецкий
математик Готфрид Вильгельм Лейбниц; он доказал, что минимальное количество букв, необходимое для кодирования любого алфавита, равно 2.
Пример. Русский язык: 33 буквы*2 (прописные, строчные)-2(ъ,ь) + 10 знаков препинания +10 цифр = 84 символа. Обязательным условием правильного кодирования является возможность однозначного преобразования А В.
Сколько двоичных символов необходимо, чтобы закодировать один символ русского языка? Предположим, для кодирования мы полбзуемся следующим правилом:
Буква |
Код |
Буква |
Код |
а |
0 |
В |
101 |
А |
1 |
… |
|
б |
10 |
м |
10010 |
Б |
11 |
М |
10011 |
в |
100 |
… |
… |
Предположим, мы закодировали слово «Мама»: 100110100100. Сделайте обратное преобразование (декодирование). Возникают проблемы, так как непонятно, где заканчивается одна буква и начинается другая. Основное правило однозначного преобразования из А в В и обратно нарушено; причина – использование кода переменной длины. Следовательно, необходимо выбрать код одинаковой, заранее определенной длины. Какой?
N – длина |
Количество |
букв, |
которое |
можно |
закодировать |
кода |
кодом длины N (=2N) |
|
|
|
|
1 |
2 |
|
|
|
|
2 |
4 |
|
|
|
|
3 |
8 |
|
|
|
|
4 |
16 |
|
|
|
|
5 |
32 |
|
|
|
|
6 |
64 (мало) |
|
|
|
|
7 |
128 (много) |
|
|
|
|
8 |
256 |
|
|
|
|
Информатика |
Пчелинцева Е.Г. |
Вывод: чем меньше букв в алфавите, тем длиннее символ. В русском языке 33 буквы, слова в среднем состоят из 4-6 букв. В японском языке около 3000 иероглифов, в среднем 1 предложение ~ 1 иероглиф.
В вычислительных машинах используется двоичное кодирование информации любого типа: программы, текстовые документы, графические изображения, видеоклипы, звуки и т.д. Удивительно, но все это богатство информации кодируется с помощью всего двух состояний: включено или выключено (единица или ноль). Формирование представления информации называется ее кодированием. В более узком смысле под кодированием понимается переход от исходного представления информации, удобного для восприятия человеком, к представлению, удобному для хранения, передачи и обработки. В этом случае обратный переход к исходному представлению называется декодированием.
При любых видах работы с информацией всегда идет речь о ее представлении в виде определенных символических структур. Наиболее распространены одномерные представления информации, при которых сообщения имеют вид последовательности символов. Так информация представляется в письменных текстах, при передаче по каналам связи, в памяти ЭВМ. Однако широко используется и многомерное представление информации, причем под многомерностью понимается не только расположение элементов информации на плоскости или в пространстве в виде рисунков, схем, графов, объемных макетов и т.п., но и множественность признаков используемых символов: цвет, размер, вид шрифта в тексте.
Кодирование текста осуществляется с помощью специальных программных кодовых таблиц. Каждому символу латинского и русского алфавита соответствует свое уникальное число. Можно назвать его номером. Для символов латинского алфавита существует одна кодовая таблица для всех компьютеров и всех операционных систем. Для русского языка это не так. Например, русские тексты, созданные в операционной системе MS DOS нельзя просматривать в операционной системе WINDOWS без специального преобразования. Для стандартизации кодировки был разработан код ASCII (Американский стандартный код для информационного обмена). Это набор восьмибитовых чисел, который жестко определяет 128 символов для латинского алфавита и некоторых специальных символов, а коды от 128 до 255 предназначены для кодирования символов национальных алфавитов других стран, в том числе и России.
Итак, когда на клавиатуре компьютера нажимается какая-либо клавиша, то в оперативную память передается код этой клавиши, а затем с помощью специальной программы он передается некоторому устройству, например видеокарте, которая генерирует поточечное изображение символа на экране монитора. Внешний вид изображения символов на экране также определяется с помощью программы. Такая программа называется драйвером.
Информатика |
Пчелинцева Е.Г. |
Драйвер – это программа-посредник между оборудованием и другими программами.
Таким образом, тексты хранятся на диске или в памяти в виде чисел и программным способом преобразовываются в изображения символов на экране.
1.6.1.Кодирование изображений
В1756 году выдающийся русский ученый Михаил Васильевич Ломоносов (1711 - 1765) впервые высказал мысль, что для воспроизведения любого цвета, имеющегося в природе, достаточно смешать в определенных пропорциях три основных цвета: красный, зеленый, синий. Теория трехкомпонентности цвета утверждает, что в зрительной системе человека возникают нервные возбуждения трех типов, каждое из которых независимо от остальных.
Компьютерное кодирование изображений также построено на этой теории. Картинка разбивается вертикальными и горизонтальными линиями на маленькие прямоугольники. Полученная матрица прямоугольников называется растром, а элементы матрицы – пикселями (от англ. Picture's element – элемент изображения). Цвет каждого пикселя представлен тройкой значений интенсивности трех основных цветов. Такой метод кодирования цвета называется RGB (от англ. red – красный, green – зеленый, blue – синий). Чем больше битов выделено для каждого основного цвета, тем большую гамму цветов можно хранить про каждый элемент изображения. В стандарте,
называемом true color (реальный цвет), на каждую точку растра тратится 3 байта, по 1 байт на каждый основной цвет. Таким образом, 256 (=28) уровней яркости красного цвета, 256 уровней яркости зеленого цвета и 256 уровней яркости синего цвета дают вместе примерно 16,7 млн различных цветовых оттенков. Это превосходит способность человеческого глаза к цветовосприятию.
Чтобы хранить всю картинку, достаточно записывать в некотором порядке матрицу значений цветов пикселей, например, слева направо и
сверху вниз. Часть информации о картинке при таком кодировании потеряется. Потери будут тем меньше, чем мельче пиксели. Для компьютерных мониторов с диагональю 15 - 17 дюймов разумный компромисс между качеством и размером элементов картинки на экране обеспечивает растр в 768х1024 точки.
При кодировании изображений не всегда используются именно три основных цвета. При печати картинок (и при рисовании) на бумаге, если смешать красную и зеленую краски, получится не желтый, а коричневый цвет. Это происходит потому, что краски сами по себе не отражают света, а только поглощают некоторые цвета из падающего на них светового потока. Поэтому в качестве основных применяются другие цвета: голубой, сиреневый и желтый, а метод кодирования цвета называется CMY (от англ. cyan – голубой, magenta – сиреневый, yellow – желтый). При этом красный
Информатика |
Пчелинцева Е.Г. |
цвет получается как сумма сиреневого и желтого, а зеленый – как сумма желтого и голубого.
Так как визуальное восприятие цвета является трехкомпонентным, то всякий цвет может быть задан не менее чем тремя параметрами. Во многих программах обработки изображения используется более приближенная к человеческому восприятию схема кодирования HSV (от англ. hue – цветовой тон, saturation – насыщенность, value – величина, яркость). Часто вместо HSV используется обозначение HSB (brightness – яркий, светлый).
Цветовой тон – близость цвета к тем или иным цветам спектра. Насыщенность – степень выраженности тона в цвете, т.е. насколько к данному спектральному цвету примешан одинаковый с ним по яркости белый цвет. Яркость (светлота) определяется уровнем действующего на глаз излучения. Если одна часть объекта освещена прямым светом, а другая – рассеянным от того же источника, то цвета воспринимаются человеком поразному, несмотря на то, что цветовой тон и насыщенность этих частей одинаковы.
Кодировка с помощью цветового тона, насыщенности и яркости позволяет легко получить из цветной монохромную, или, как не совсем верно говорят, черно-белую, не меняя яркости объектов изображения.
В 80-х годах рынок персональных компьютеров был фактически захвачен клонами компьютеров IBM PC. Вехой в развитии самих IBM PC явился разработанный в 1987 году стандарт VGA (англ. Video graphics Array
– дословно «видеографическая матрица или массив»). Видеоадаптеры, платы, осуществляющие преобразование информации в изображение на экране, стали использовать более высокое разрешение (640х480 точек) и большую глубину представления цвета на мониторе (256 цветов вместо 16).
Стандарт VGA комплектовался памятью 256 Кбайт, где поэлементно хранились картинки, образованные горизонтальными строками развертки на дисплее.
Для увеличения растра, например до 800х600 точек, при сохранении глубины цвета 8 бит на точку (256 цветов) требовалось увеличить объем памяти в 2 раза (800х600= 480 000 точек, т.е. около 480 Кбайт). При растрах
1024х768, 1280х1024, 1600х1200 памяти надо еще больше. 256 цветов недостаточно для получения полноценной картинки, поэтому глубина цвета была увеличена: 16 бит на точку – high color (лучший цвет), 24 бит на точку – true color (настоящий, реальный цвет).
Легко подсчитать, что если на каждую точку приходится по 24 бит, т.е. 3 байта, то для хранения картинки 800х600 точек потребуется около 1,4 Мбайт (800х600х3= 1440000). Это неэкономно, если фигура небольшая, например треугольник.
Достоинства растровых изображений – в их способности передать тончайшие нюансы изображения, а также в широчайших возможностях по его редактированию, выражающихся в простом доступе к каждому пикселю изображения, возможности индивидуального изменения каждого из его
