4. Вычисление прогиба и расчет на жесткость

Расчет на неподвижные нагрузки завершается вычислением прогиба в середине наибольшего пролета заданной балки по формуле Мора:

где – расчетная эпюра изгибающих моментов от заданных нагрузок

(рис. 3г);

–эпюра изгибающих моментов единичного состояния, построенная от силы = 1, приложенной в середине наибольшего пролета;

Сначала определяем пролеты заданной балки, то есть расстояния между соседними наземными опорами. В нашем примере (рис. 3а) они будут равны l_AB = 9м, l_BE = 12м, l_ЕЖ = 5м. Отсюда следует, что середина наибольшего пролета находится на расстоянии 6м от опоры В в сторону опоры Е. Приложив в этом сечении = 1, строим от ее действия эпюру изгибающих моментов вспомогательного состояния (рис. 7).

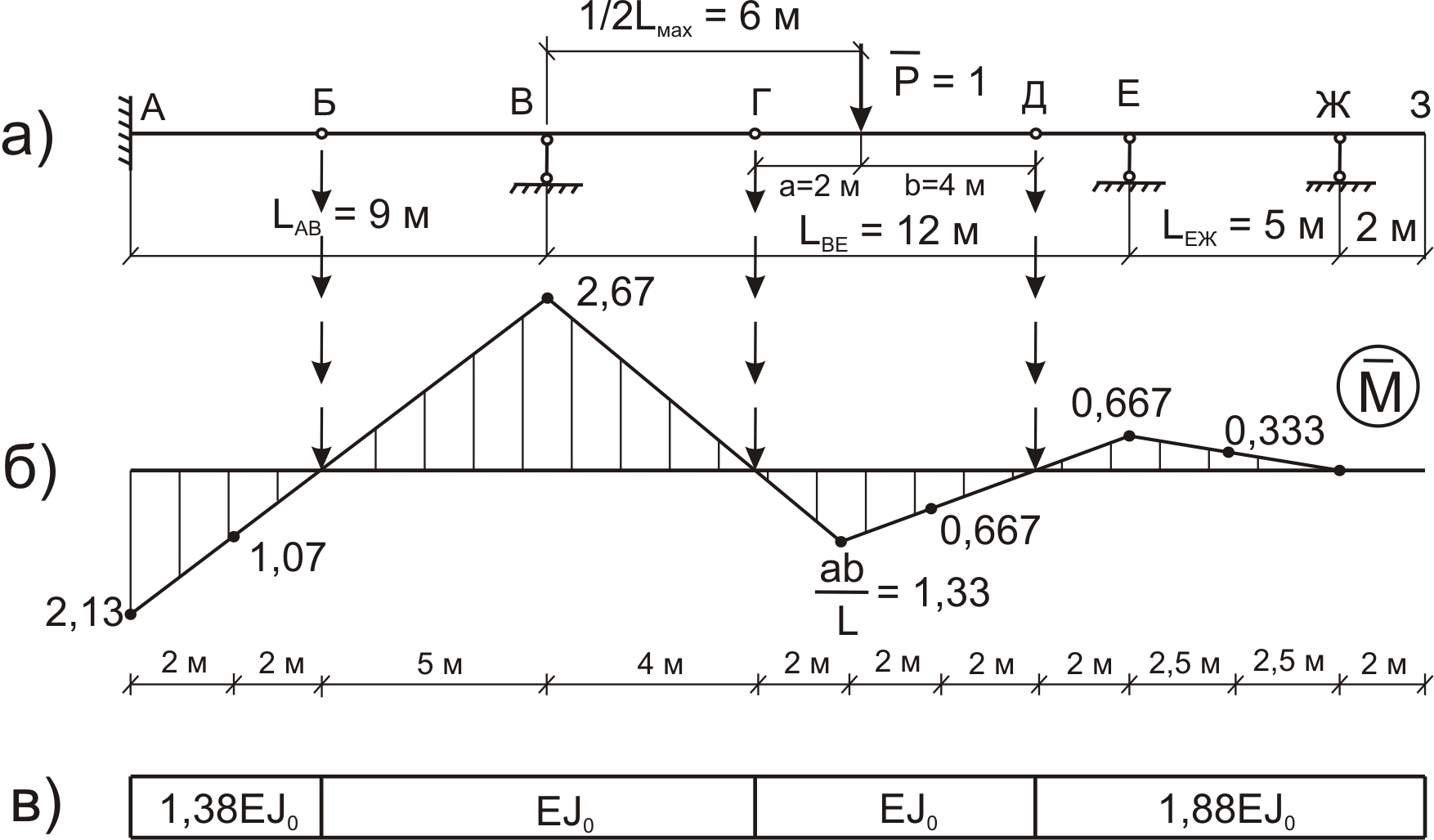
Рис. 7

Порядок построения эпюрыпринципиально не отличается от последовательности построения эпюры М от действия внешних нагрузок. Но здесь можно воспользоватьсяупрощенным приемом, основанном на том, что на всех участках балки, между внешними сосредоточенными силами (= 1 иV_i), эпюра является линейной, а в сечениях Б, Г, Д (совпадающих с шарниром) изгибающие моменты должны быть равными нулю. Кроме того, в сечении Ж изгибающий момент также равен нулю, так как консоль Ж-З в единичном состоянии не загружена (рис. 7а). Перенесем полученные нулевые точки Б, Г, Д, Ж на график эпюры(на рис. 7), как показано вертикальными стрелками, и вычисли ординату эпюрыпод единичной силой по формуле сопротивления материалов =Р_ab/l = 1·2·4/6 = 1,33 кНм (максимальный изгибающий момент в свободноопертой балке Г – Д от Р = 1). Эта ордината (играющая роль масштабного отрезка) соединяется прямыми линиями с нулевыми точками Г и Д и продолжается до вертикалей В и Е, где приложены реактивные силы и. Здесь линейные эпюры претерпевают излом и проходят через следующие нулевые точки Б и Ж. На консоли Ж – З внутренние усилия отсутствуют, т.к. консоль в единичном состоянии не загружена.

Используя описанный прием, следует учитывать особенности конкретной «поэтажной» схемы и положения единичной силы. Так, если бы сила = 1 была приложена на консоли В – Г, то изгибающий момент на опоре В был бы равен плечу действия силы относительно опоры. Эпюра изменялась бы линейно от нуля под силой до перелома над опорой В и даже проходила бы через нулевую точку Б до конца балки. Правее силы (в том числе на балках Г – Д и Д – З) она была бы нулевой (рис. 8а). На рис. 8б, в показаны некоторые другие характерные случаи упрощенного построения эпюр .

После построения эпюры М и определения относительных изгибных жесткостей участков (рис. 7в): EJ_АБ = 1,36 EJ₀; EJ_БА = EJ₀, EJ_АЗ = 1,88 EJ₀ (изгибные жесткости выражены через EJ₀ = 3864 кНм²), вычисляется искомый прогиб. При этом на простых линейных участках эпюр удобно использовать прием А.Н. Верещагина. На сложных параболических – формулу Симпсона (ниже такие члены выделены одной чертой), при «перемножении» трапеции – формулу трапеций (выделено двумя чертами).

Рис.8

Отсюда относительный прогиб равен f/l = 6,57 см /1200 см = 1/183, что по условиям эксплуатации сооружений является недопустимым. Предельные относительные прогибы составляют для рассматриваемых балок 1/500 ÷ 1/700. Поэтому из условия жесткости в целях исключения чрезмерных деформаций необходимо развить поперечное сечение до

EJ_0треб = 253,85 · 700 / 12 = 14808 кНм², т.е. J_0треб = 7051 см⁴ . Или по участкам (рис. 7в) J_АБтр = 9589 см⁴, J_БДтр = 7051 см⁴, J_ДЗтр = 13256 см⁴. На участке А – Б принимаем двутавр №36 (J_АБ = 13380 см⁴ ), на участке Б – Д двутавр №30 (J_БД = 7080 см⁴ ), на Д – З №40 (J_ДЗ = 19062 см⁴ ). Следует подчеркнуть, что условия жесткости сооружений, особенно транспортных, вызывают дополнительные затраты материалов. Так, в нашем примере увеличение начальных поперечных сечений балок F_jⁿ до последних F_j^ж на каждом участке длиной i_j приводит к возрастанию материалоемкости конструкции на ∆G процентов:

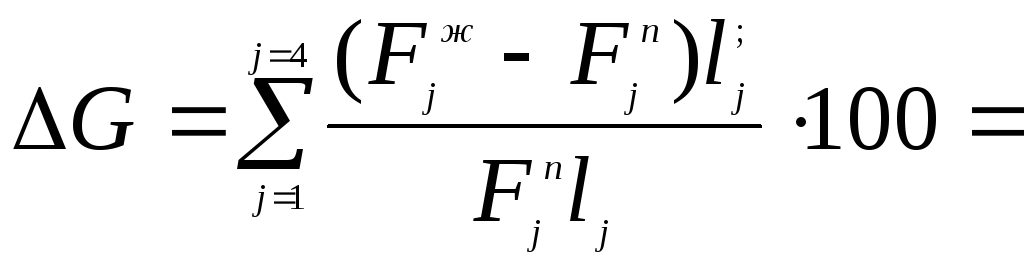((61,9 – 30,6) · 400 + (46,5– 23,4) ·1500 +

+ (72,6 – 34,8) · 900) ·100 / (30,6 ·400 + 23,4 · 1500 + 34,8 · 900) = 103,2 %.

Этот пример подчеркивает необходимость поиска более рациональных решений расчетно-проектировочной задачи. В частности, путем подбора рационального распределения жесткостей EJ_j по участкам; целенаправленного изменения структуры расчетной схемы; введения дополнительных связей и т.д.