
Зразок виконання індивідуального завдання
1. Ймовірність того, що електротехнічний прилад зажадає ремонту в гарантійний строк, дорівнює 0,25. Знайти ймовірність того, що протягом гарантійного строку з семи приладів зажадають ремонту m = 0, 1, 2, ...; зажадають ремонту не більш чотирьох, не менш двох, більше двох і менше шести приладів.
Рішення. У цьому завданні p = 0,25 , q = 1 - p = 0,75 , n = 7 (n < 30), тому застосовуємо формулу Бернуллі:
![]() .
.
Для m = 0, 1, 2, ..., 7 обчислення зведені в таблицю, в останньому стовпчику якої наведені значення накопиченої суми ймовірностей (значення кумуляти) F(m). Нагадуємо, що функція розподілу (кумулята) визначена як F(m) = P(X m), тому F(0) = Pn(0) = 0,133484.
|
m |
Cnm |
pm |
qn–m |
Pn(m) |
F(m) |
|
0 |
1 |
1 |
0,133484 |
0,133484 |
0,133484 |
|
1 |
7 |
0,25 |
0,177979 |
0,311462 |
0,444946 |
|
2 |
21 |
0,0625 |
0,237305 |
0,311462 |
0,756409 |
|
3 |
35 |
0,015625 |
0,316406 |
0,173035 |
0,929443 |
|
4 |
35 |
0,003906 |
0,421875 |
0,057678 |
0,987122 |
|
5 |
21 |
0,000977 |
0,5625 |
0,011536 |
0,998657 |
|
6 |
7 |
0,000244 |
0,75 |
0,001282 |
0,999939 |
|
7 |
1 |
0,000061 |
1 |
0,000061 |
1,000000 |
За допомогою цієї функції ймовірність потрапляння випадкової величини в інтервал m1 < m m2 обчислюється як різниця значень функції розподілу на краях цього інтервалу: P(m1 m m2) = F(m2) - F(m1-1). Обчислюємо: P(m 4) = F(4) = 0,987122; P(m 2) = P(2 m 7) = F(7) - F(1) = 1 - 0,444946 = 0,555054; P(2<m<6) = P(3m5) = F(5) - F(2) = 0,998657 - 0,756409 = 0,242248. Додатково обчислюємо характеристики розподілу Бернуллі:
M(m)
= np
= 70,25
= 1,75; D(m)
= npq
= 70,250,75
= 1,3125; ![]() .
.
M(m) - q Mo M(m) + p; 1,75 - 0,75 Mo 1,75 + 0,25; 1 Mo 2; P(1)=P(2)=Pmax .
Відповідно до правила "трьох сигм" ймовірні значення m не перевищують M(m) + 3m = 1,75 + 31,146 = 5,19 5.
Нижче наведений графік полігона розподілу ймовірностей P(m):
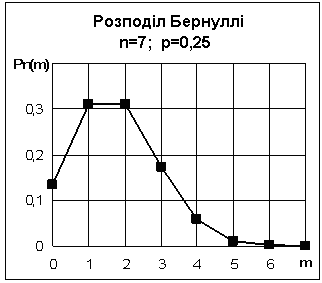
2. В одному кубічному метрі повітря в середньому знаходиться 1000 хвороботворних мікробів. На аналіз узято 2 літри (дм3) повітря. Знайти ймовірність того, що в пробі буде виявлене m = 0, 1, 2, ... хвороботворних мікробів, не більше трьох мікробів, від двох до п'яти мікробів, хоча б один мікроб.
Рішення. Ця задача на розподіл Пуассона:
![]() ,
,
де а =21000/1000 = 2 – середній зміст мікробів в 2-х літрах повітря.
Обчислення зручно робити по рекурентним формулам:
![]()
Можливі значення m
не обмежені зверху, проте, відповідно
до правила "трьох сигм", досить
розрахувати ймовірності P(m)
для ![]() .
.
Для m = 0, 1, 2, ..., 10 обчислення зведені в таблицю, поруч побудований графік:
|
m |
P(m) |
F(m) |
|
|
0 |
0,135335 |
0,135335 | |
|
1 |
0,270671 |
0,406006 | |
|
2 |
0,270671 |
0,676676 | |
|
3 |
0,180447 |
0,857123 | |
|
4 |
0,090224 |
0,947347 | |
|
5 |
0,036089 |
0,983436 | |
|
6 |
0,012030 |
0,995466 | |
|
7 |
0,003437 |
0,998903 | |
|
8 |
0,000859 |
0,999763 | |
|
9 |
0,000191 |
0,999954 | |
|
10 |
0,000038 |
0,999992 |
За допомогою функції розподілу F(m) обчислюємо: P(m 3) = F(3) = 0,857123; P(2m5) = F(5) - F(1) = 0,983436 - 0,406006 = 0,57743; P(m1) = 1 - P(0) = 1 - 0,135335 = 0,864665.
Додатково обчислюємо характеристики розподілу Пуассона:
M(m)
= a
= 2; D(m)
= a
= 2; ![]() .
.
a - 1 Mo a; 1 Mo 2; P(1) = P(2) = Pmax.
3. Серед виробів деякого заводу 75% – першого сорту. Знайти ймовірність того, що з 800 виробів першосортних виробів буде а) 600; б) не менше 590; в) не більше 620; г) не менше 590 і не більше 620. Які відхилення відносної частоти m/n виробів першого сорту від її теоретичної долі у сукупності (75%) можна очікувати з рівнем довіри а) 95%; б) 99%? Скільки потрібно взяти виробів, щоб з ймовірністю 90% можна було стверджувати, що відхилення відносної частоти m/n від її теоретичної долі 75% не буде перевищувати: а) 5%; б) 1%?
Рішення. У цьому завданні p = 0,75; q = 1 – p = 0,25; n = 800 > 30; np = 8000,75 = 600 > 5; nq = 8000,25 = 200 > 5, отже, ймовірності можна обчислювати за асимптотичними формулами Лапласа:
![]() ,
,
де ![]() –диференційна функція Лапласа;
–диференційна функція Лапласа;
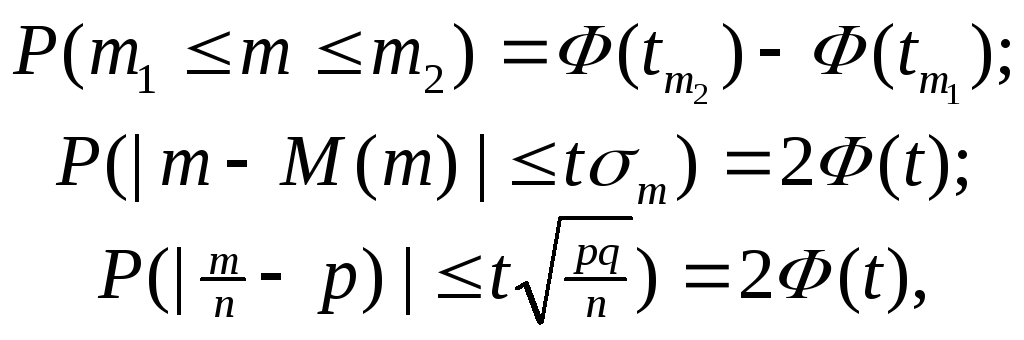
де ![]() – інтегральна функція
Лапласа.
– інтегральна функція
Лапласа.
Обчислюємо:
M(m)=np=8000,75=600;
![]()
![]()
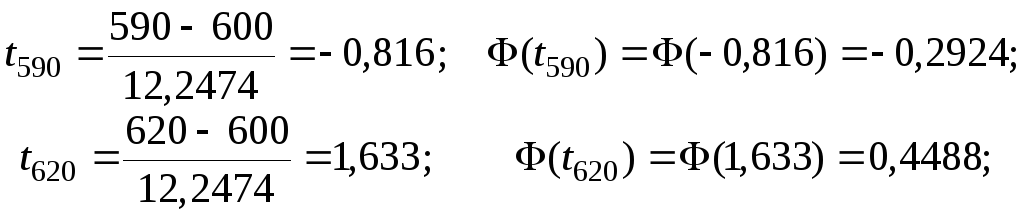
![]()
![]()
![]()
Відповіді на питання, що залишилися, можна одержати за допомогою "третьої форми інтегральної теореми Лапласа":
![]()
При рівні довіри Р=0,95 Ф(t)=0,475,
звідки t=1,96 і ![]()
При рівні довіри Р=0,99 Ф(t)=0,495,
звідки t=2,58 і ![]()
В останнім питанні задане рівень довіри Р=0,9 і гранична погрішність = 0,05; = 0,01.
При рівні довіри Р=0,90
Ф(t)=0,45,звідки t=1,64 і ![]()
Якщо = 0,05,то
![]() ,
тобто необхідно взяти n=202
вироби.
,
тобто необхідно взяти n=202
вироби.
Якщо = 0,01,то
![]() ,
тобто необхідно взяти n=5043
виробів.
,
тобто необхідно взяти n=5043
виробів.

