Лекция по теории систем 3

Лекция № 3 Понятие системы с точки зрения макроподхода. Операторы. Принцип суперпозиции

Микроподход предполагает рассмотрение объекта «изнутри» на основе изучения протекающих в нем процессов.

Динамической системой å называется сложный математический объект, определяемый следующими аксиомами:

аксиома а: заданы множества:

моментов времени Т; состояний Х; входных воздействий U; допустимых входных воздействий W; выходных значений Y; выходных функций Г.

аксиома б: задано направление времени, т.е. Т - упорядоченное подмножество множества действительных чисел.

аксиома в: множество допустимых входных воздействий W удовлетворяет следующим условиям:

1. W - непустое;

2. Для воздействий ÎW, в моменты времени , существует такое на, что , при и при

аксиома г: Задана переходная функция состо-яния j, которая определяет состояние , достигнутое в момент времени , при , если в момент вре-мени имелось состояние: .

Свойства функции j :

Направление времени: j определена при , и необязательно определена при .

Согласованность:

,

Свойство композиции:

Для , :

Свойство причинности: Если есть такие, что при , то

.

аксиома д: Существует отображение выхода h, которое таково: .

Тогда система может быть формально задана следующим образом:

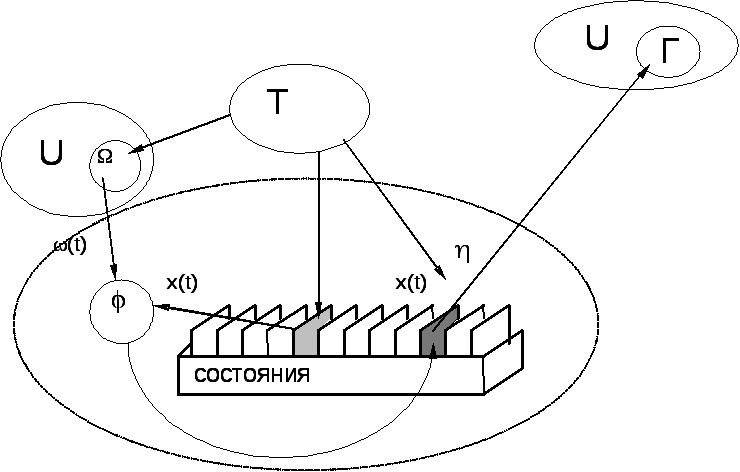
Говорят, что пара задает оператор функционирования системы. На рисунке показано формирование реакции системы с помощью переменных состояния в соответствии с микроподходом.

Оператор А задан, если установлено прави-ло по которому любому элементу из множества U ставится в соответствие элемент из множества Y и при этом Y не является множеством чисел.

Способы записи оператора:

1. ;

2. К применен оператор А; реакция - ;

3. ;

4. .

Примеры операторов

1. Оператор дифференцирования: .

2. Оператор интегрирования: .

Любой динамической системе может быть поставлен в соответствие оператор.

Операторы разделяются на два класса: нелинейные операторы и линейные операторы.

Оператор называется линейным если для не-го выполнен принцип суперпозиции, и – нели-нейным, если принцип суперпозиции для него не выполнен. Мы рассмотрим 2 формы записи этого принципа – дискретную и непрерывную.

Дискретная форма.

Непрерывная форма.

.

Запись означает, что оператор А действует в момент времени t.

Если системе соответствует линейный опе-ратор, то система называется линейной. Иначе система называется нелинейной.

Физический смысл принципа заключается в следующем: реакция линейной системы на линейную комбинацию воздействий может быть определена, как линейная комбинация реакций системы на каждое из воздействий в отдельности.

Операторы интегрирования и дифференци-рования - линейные операторы. Оператор возве-дения в квадрат: является нели-нейным оператором.

Обобщенная -функция Дирака

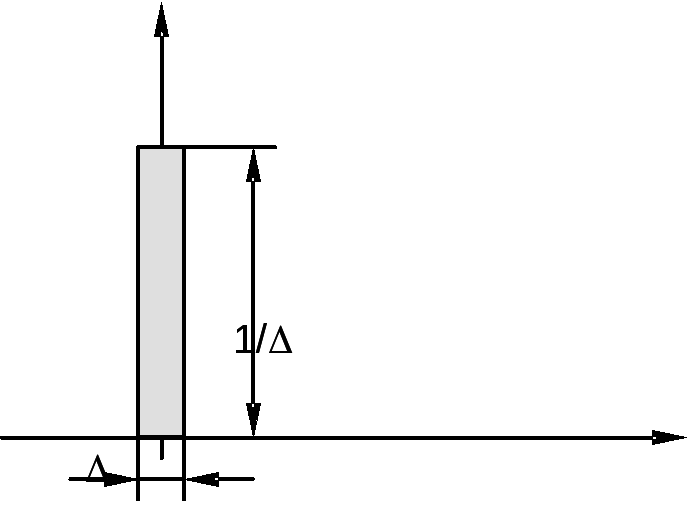
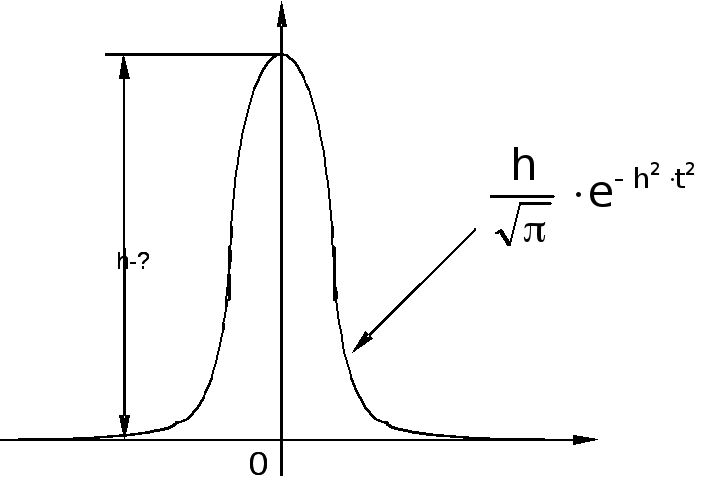
Для конструирования моделей ДС рассмотрим обобщенную -функцию Дирака и ее свойства. Определим ее так: , причем .

Возможные модели -функции:

Мы будем использовать т.н. фильтрующее свойство -функции:

Приведем доказательство этого свойства:

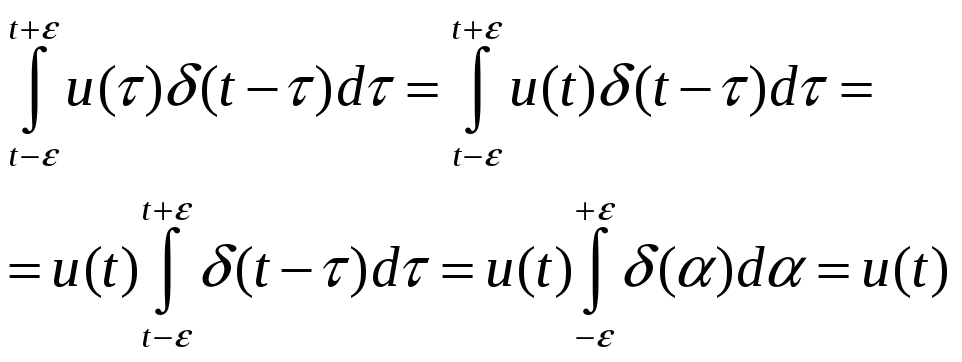
-функция связана с единичной функцией , которая задается так: . В частности и .

Применим теперь фильтрующее свойство -функции для входного процесса :

.

Этот результат можно интерпретировать как разложение процесса по бесконечному числу импульсов . Считая -функцию одним из возможных элементарных воздейст-вий, запишем реакцию системы с оператором , используя полученное разложение:

.

Если , то

Основной результат этого в следующем: введена функция , которая определя-ется как реакция системы на импульсное воздействие (т.н. импульсная переходная (весовая) функция). С ее помощью получе-на общая форма модели линейной непреры-вной системы, представляющая собой интеграл свертки весовой функции с вход-ным воздействием

Весовая функция показывает удельный вес возмущения, которое дейст-вовало на систему в момент времени на формирование реакции системы в момент времени t.