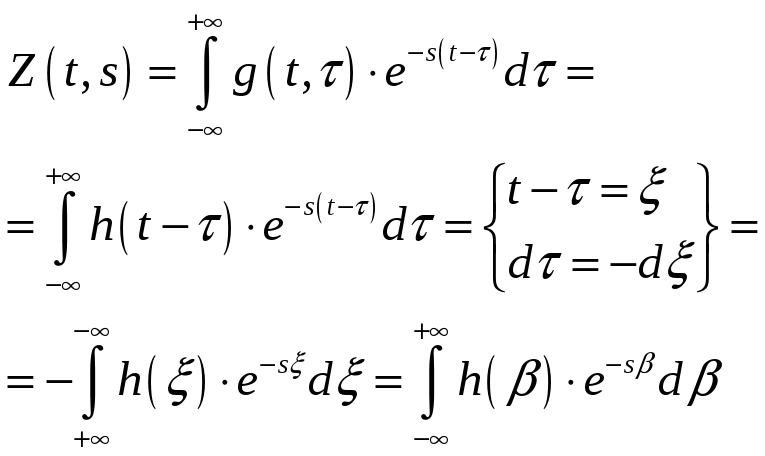Лекция по теории систем 5

Лекция №5

Характеристика реакции линейной системы на показательное воздействие

В качестве элементарных воздействий могут быть использованы не только импульсные или ступенчатые воздействия, но и другие, более сложные сигналы , такие, как гармонические. Мы рассмотрим в этом качестве показательное воздействие. Оно объединяет в себе воздействия затухающие и гармонические.

Пусть , где s - некий комплексный параметр.

Такое воздействие обобщает все остальные воздействия (почему?).

Назовем характеристикой реакции линейной системы на показательное воздействие величину:

, где - реакция линейной системы на показательное воздействие, а - само показательное воздействие.

показывает, как меняются модуль и фаза входного воздействия при его прохождении через линейную систему.

Если s - чисто мнимая величина, то задает частотную характеристику:

Задача: показать, как меняется амплитуда и фаза входного воздействия (гармонического) при прохождении через систему с заданной частотной характеристикой.

- задает амплитудно-частотную характеристику (АЧХ);

- задает фазовую частотную характеристику (ФЧХ).

Рассмотрим функцию u(t), ее интеграл Фурье имеет вид:

, где .

Найдем реакцию линейной системы на воздействие u(t).

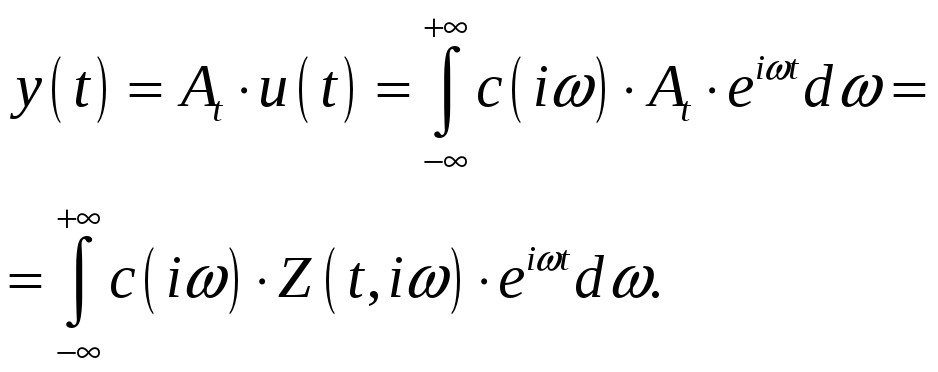
Из этого результата следует, что реакция линейной системы может быть определена через реакцию на показательное воздействие, но это, к сожалению, требует дополнительных преобразований связанных с расчетом коэффициентов . Только для импульсного воздействия эту работу делать не нужно.

Связь частотной характеристики и весовой функции

Для установления этой связи определим реакцию линейной системы на показательное воздействие при помощи весовой функции:

.

Тогда

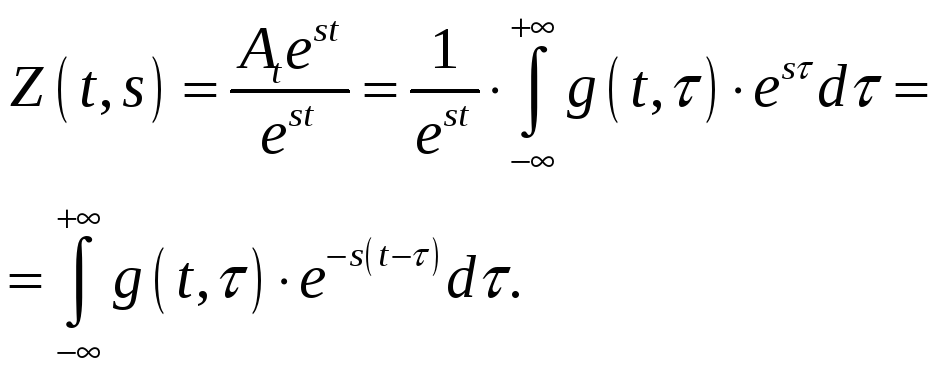
При :

Известный факт:

Это соотношение показывает, что импульсное воздействие содержит в себе гармонические колебания всех частот с одинаковыми коэффициентами. Тогда

Стационарные системы. Передаточная функция.

Для стационарных систем весовая функция зависит только от разности моментов времени:

.Тогда

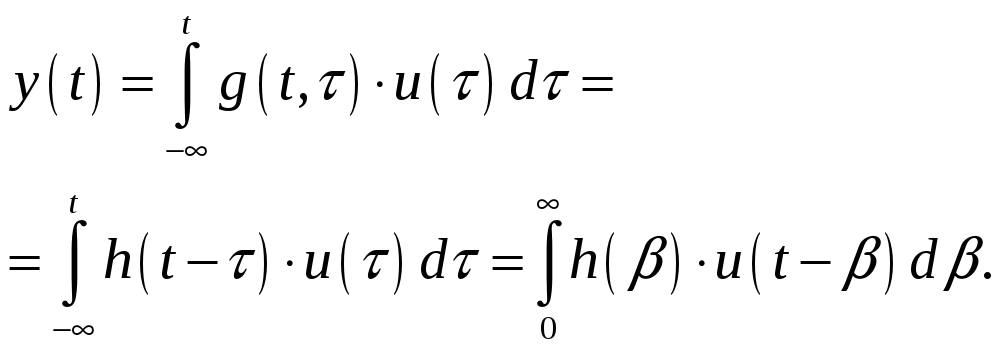
Поэтому характеристика реакции линейной стационарной системы на показательное воздействие имеет вид:

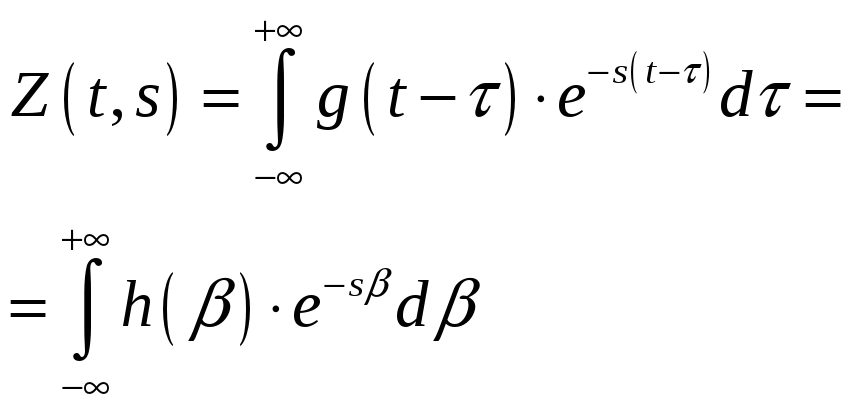
Т.е. не зависит от времени.

С учетом физической осуществимости системы, имеем:

Функцию называют передаточной функцией.

Важно что (***)

К сожалению, определяется таким образом только для воздействия !

Пример определения передаточной функции.

Рассмотрим обыкновенное дифференциальное уравнение второго порядка

.

Пусть . Тогда .

.

Получаем:

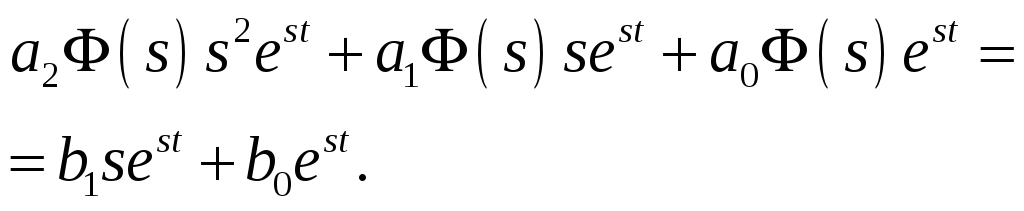
- передаточная функция; при

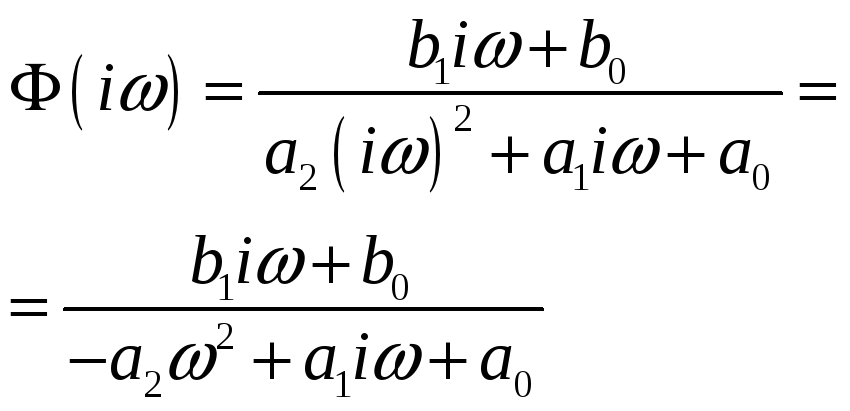
- частотная характеристика.