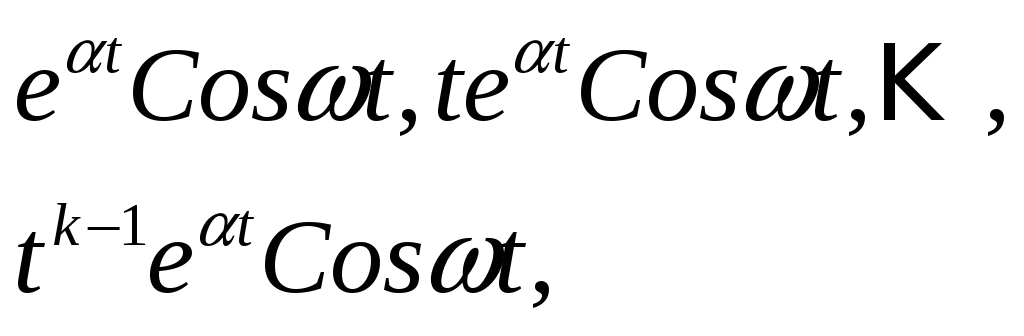Лекция по теории систем 6
.docЛекция №6. Модели линейных непрерывных систем, построенные с помощью макроподхода во временной области
Напомним: непрерывными системами (НС) называются системы, вход и выход которых являются функциями непрерывного времени.
Реакция таких систем определяется как:
![]()
Основной моделью ЛНС в макроподходе является обыкновенное дифференциальное уравнение n-го порядка.
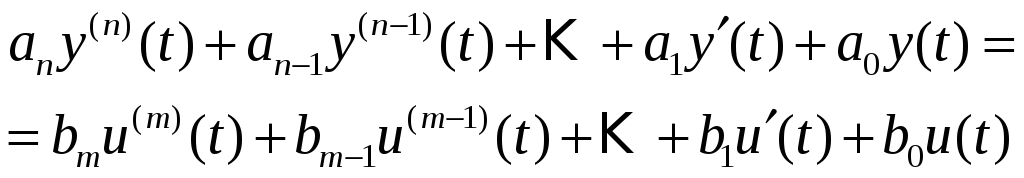 .
.
Краткая запись:![]()
(для физически
осуществимых систем
![]() ).
).
Это же уравнение в операторной форме:
![]() , (1)
, (1)
где
![]() и
и
![]() - линейные операторы.
- линейные операторы.
Решение такого
операторного уравнения может быть
получено применением слева к обеим
частям операторного уравнения обратного
к
![]() линейного оператора
линейного оператора
![]() ,
который обладает следующим свойством:
,
который обладает следующим свойством:
![]() ,
где
,
где
![]() :
:
![]() ,
,
![]() .
Т.к. линейные операторы перестановочны,
то
.
Т.к. линейные операторы перестановочны,
то
![]() .
Пусть
.
Пусть
![]() ,
т.е.
,
т.е.
![]() удовлетворяет уравнению:
удовлетворяет уравнению:
![]() ) (2),
будем иметь следующую систему операторных
уравнений:
) (2),
будем иметь следующую систему операторных
уравнений:
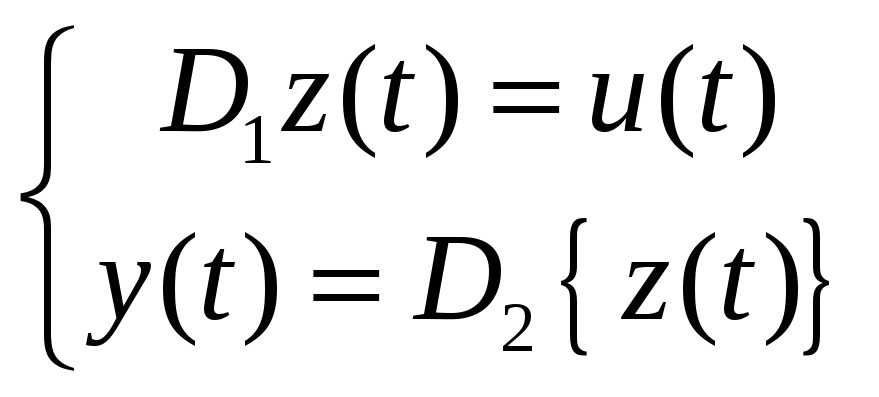 .
Определим для первого уравнения весовую
функцию, приложив входное воздействие
.
Определим для первого уравнения весовую
функцию, приложив входное воздействие
![]() ,
тогда реакция
,
тогда реакция
![]() .
Т.к. одновременно реакция
.
Т.к. одновременно реакция
![]() -
весовая функция системы (1), то будем
иметь:
-
весовая функция системы (1), то будем
иметь:
![]() .
.
Перечислим основные
этапы определения весовой функции
![]() системы (1):
системы (1):
-
Для системы (2) (она не выполняет дополнительного преобразования входного воздействия) определить весовую функцию
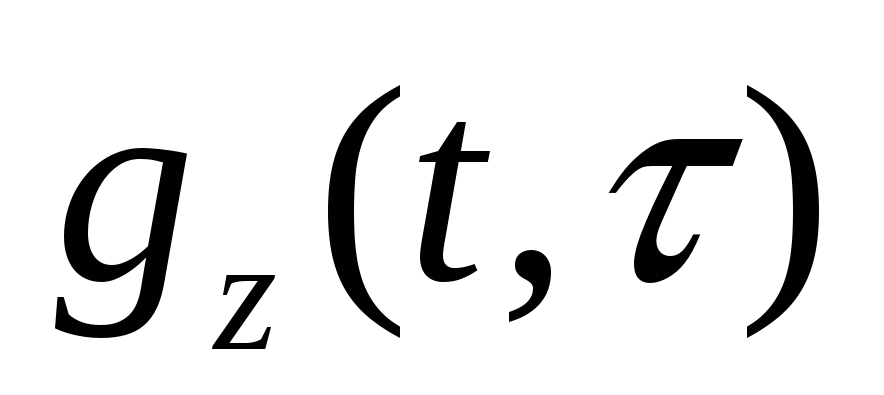 ,
положив
,
положив
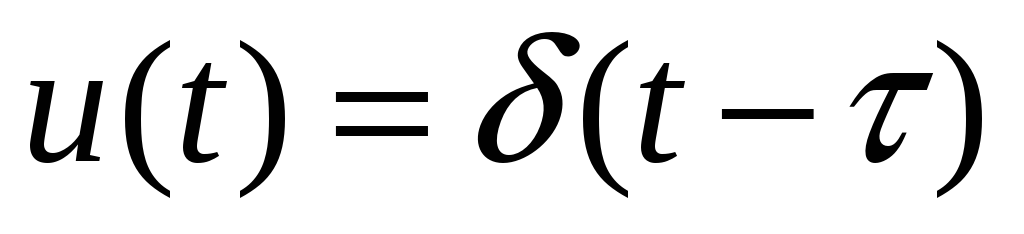 .
. -
Применить оператор правой части (1) к
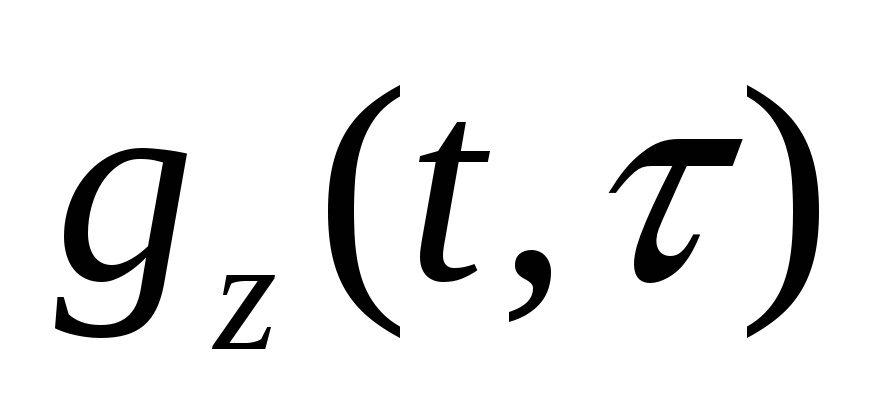 :
:
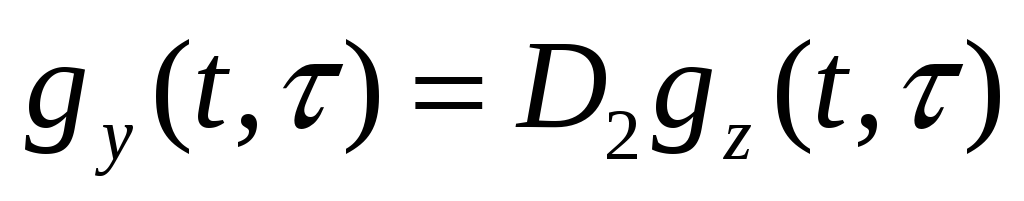
Таким образом, вместо изучения системы (1) достаточно изучить систему (2).
Рассмотрим систему,
описываемую операторным уравнением
![]() ,
или в обычной форме:
,
или в обычной форме:
![]() (3)
(3)
с заданными
начальными условиями
![]() .
.
Т. к. рассматриваемая
система является линейной, то, в
соответствии с теорией обыкновенных
дифференциальных уравнений, полное
решение
![]() может быть получено как наложение двух
решений
может быть получено как наложение двух
решений
![]() ,
,
где
![]() – общее решение однородного уравнения
(
– общее решение однородного уравнения
(![]() )
с заданными начальными условиями;
)
с заданными начальными условиями;
![]() – частное решение
неоднородного уравнения (с нулевыми
начальными условиями).
– частное решение
неоднородного уравнения (с нулевыми
начальными условиями).
Определение
![]() .Функция
.Функция
![]() есть
линейная комбинация n
линейно независимых решений, определяемых
левой частью дифференциального уравнения
есть
линейная комбинация n
линейно независимых решений, определяемых
левой частью дифференциального уравнения
![]() (4)
(4)
В предположении,
что функции
![]() являются решениями уравнения (4), получаем
для s
алгебраическое уравнение:
являются решениями уравнения (4), получаем
для s
алгебраическое уравнение:
![]() (5),
(5),
которое называют характеристическим уравнением, а многочлен в левой части – характеристическим многочленом, т.е. параметр s должен быть корнем характеристического уравнения. Из основной теоремы алгебры известно, что уравнение (5) имеет n корней, которым соответствуют n линейно независимых решений, которые приведены в таблице:
Табл.1.
|
Свойства корня |
Соответствующие решения |
|
s – действительный корень кратности 1 |
|
|
s – действительный корень кратности k |
|
|
s
– комплексно сопряженный корень
кратности 1:
|
|
|
s
– комплексно со-пряженный корень
кратности k
|
|
Решение уравнения (4) имеет вид:
![]() ,
где
,
где
![]() –
решения, соответствующие корням уравнения
(5).
–
решения, соответствующие корням уравнения
(5).
Произвольные
постоянные
![]() определяются с помощью начальных
условий, приложенных к системе, как
решение следующей системы линейных
алгебраических уравнений:
определяются с помощью начальных
условий, приложенных к системе, как
решение следующей системы линейных
алгебраических уравнений:
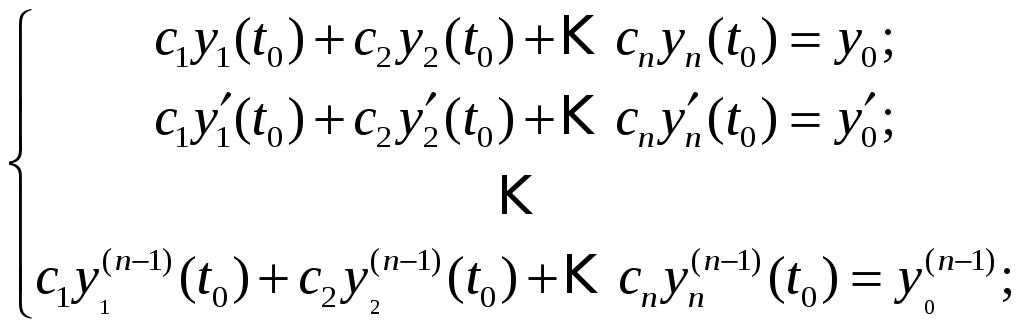
Определение
![]() .
Мы рассмотрим
всего два подхода, из которых
предпочтительней для дифференциальных
уравнений будет второй.
.
Мы рассмотрим
всего два подхода, из которых
предпочтительней для дифференциальных
уравнений будет второй.
Первый подход.
Основывается на
идеологии исследования линейных систем
с неизвестной структурой и заключается
в изучении реакции системы при нулевых
начальных условиях при предъявлении
на вход системы импульсного воздействия
![]() и реализации
этапов, описанных в начале данной лекции.
и реализации
этапов, описанных в начале данной лекции.
Второй подход.
Подход основывается на идее, в соответствии с которой весовая функция в случае стационарности определяется в виде:
![]() ,
т.е. по форме ровно так же, как и общее
решение дифференциального уравнения,
однако начальные условия должны быть
выбраны специальным образом, а именно:
,
т.е. по форме ровно так же, как и общее
решение дифференциального уравнения,
однако начальные условия должны быть
выбраны специальным образом, а именно:
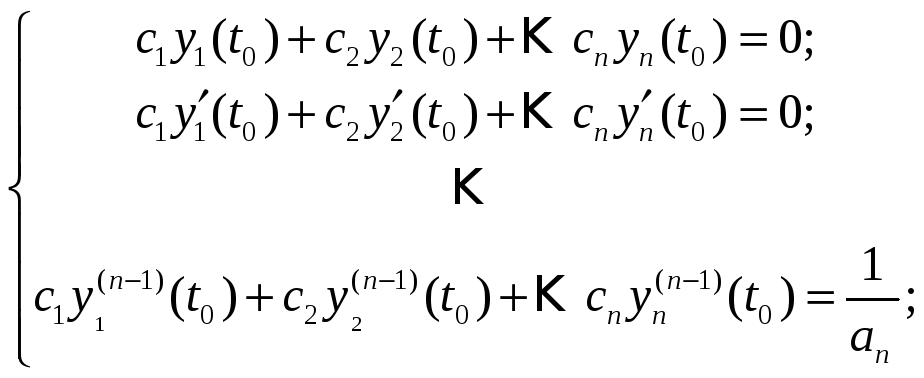
Достаточно просто
можно показать, что импульсное воздействие
на входе системы при нулевых начальных
условиях и специальным образом выбранные
начальные условия при нулевом входном
воздействии порождают одинаковые
результаты. Поэтому
![]() .
.
(Предложите доказательство сформулирован-ного утверждения).