Добавил:

star Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Аналитическая геометрия и линейная алгебра

Файл:

Лекция Многочлены 2 МО-1

.pdf

Скачиваний:

Добавлен:

22.08.2023

Размер:

971.57 Кб

Скачать

☆

Лекция «Многочлены (продолжение)»

Деление многочленов с остатком

Эта теория во многом совпадает с соответствующей теорией целых чисел. А именно: на множестве многочленов, так же как и на Z, вводятся операция деления с остатком, понятия делимости, наибольшего общего делителя, взаимно простых элементов и т. п., причем основные результаты (и часто их доказательства) практически идентичны (с некоторыми оговорками).

При ручных вычислениях алгоритм деления многочленов обычно реализуется с помощью схемы деления уголком.

Пример. Разделим f(x) = 2x4 −10x3 + 23x2 − 22x − 3 на g(x) = x2 − 3x + 5 с остатком:

Если мы обозначим q(x) = 2x2 − 4x + 1, а r(x) = x − 8, то мы можем представить f(x) в следующем виде:

			f(x) = g(x) q(x) + r(x).
Теорема Пусть f ,g C x , g 0. Тогда !q,r C x :
f q g r			, причем r(x) = 0 или degr degg.
Доказательство:
Пусть deg f n,	degg m.
Если n m, то можно положить				q x 0, r x f x .
Если n m, то будем использовать тот же метод деления, что и для чисел.
Пусть
f x a	n	xn a , g x b xm b ,				a	n	0 и b	0.
	n		0	m	0		n	m

Положим f x f x	an	xn mg x .

1	bm

Тогда deg f1 n.

Пусть deg f

n и

f x a

xn1 a .

Если n1 m, то остановим процесс вычисления;

если n m,

то положим f

an1

xn1 mg x .

Пусть n2 deg f2 ,

an2

– старший коэффициент f2,

Если n2 m, то остановим процесс вычисления;

если n

m, то положим f

an2

xn2 mg x .

и т.д. …

Так

как

степени

многочленов

f1, f2, убывают, то получим

fk :

x f

k 1

ank 1

xnk 1 mg x и n m.

Процесс останавливается.

Суммируя полученные ранее выражения, получаем:

k 1

f x

xn m

xn1

xnk 1

m g x f

x .

Тогда q x

xn m

xn1 m

k 1

xnk 1

m ,

r x fk x , т.е.

получено требуемое

представление f(x).

Докажем единственность.

Пусть f q1g r1 и f q2g r2.

Тогда q1 q2 g r2 r1.

Если q1	q2	, то и r1 r2.
Если q1	q2	, то deg q1 q2 0
deg q1 q2 g m, a deg r2 r1 m противоречие q1 q2,			r1 r2 .

Замечание Из указанного в теореме алгоритма деления с остатком следует, что если f x и g x – многочлены с действительными коэффициентами, то коэффициенты всех многочленов f1 x , f2 x , , а значит и коэффициенты q x и r x – действительные.

Определение Если f gq r и degr degg или r(x)=0 , то f(x) называется делимым, g(x) − делителем, q(x) − частным, r(x) − остатком при делении f x на g x .

	Определение Будем говорить, что f x делится на	g x , если остаток при делении
r(x) = 0.
	Обозначать будем f(x) g(x) ,
а g(x)	f(x) обозначение f(x) делит g(x) без остатка.

Корни многочленов

Определение Число с C называется корнем f(x) C[x], если f(c)=0.

Теорема (теорема Безу).

Пусть f(x) C[x]. Остаток от деления f(x) на x c равен f(c). Доказательство:

Разделим f(x) на x c.

По предыдущей теореме f (x) (x c)q(x) r(x)и остаток r(x) либо нулевой, либо

deg r(x)<deg (x c)=1.

1)Если r(x)=0, то f (x) (x c)q(x) и f(c)=0= r(x),

2)Если deg r(x)<deg (x c)=1, то r(x) С, r(x) r. f (x) (x c)q(x) r r = f(c).

СледствиеПусть f(x) C[x], тогда f(c)=0 f(x) делится на x c Доказательство:

Т.к. f (x) (x c)q(x) f (c),

То если f(c)=0, то f (x) (x c)q(x), т.е. f(x) делится на x c,

В обратную сторону, если f(x) делится на x c, то f (x) (x c)q(x) f(c)=0.

Определение Число с C называется корнем кратности k многочлена f(x) C[x], если f(x) делится на (x c)k и не делится на (x c)k+1.

Если k =1, то корень называется простым, k =2 двойным и т.д..

Схема Горнера

Многочлен f(x) можно разделить на x c с остатком и заодно найти значение f(c), используя так называемую схему Горнера. Пусть f(x) имеет вид:

f(x) = an xn + an-1xn-1 +…+ a1 x+a0,

тогда f (x) (x c)q(x) f (c), где q(x) = bn-1xn-1 +…+ b1 x+b0.

Приравнивая левую и правую часть:

an xn + an-1xn-1 +…+ a1 x+a0=(x c)( bn-1xn-1 +…+ b1 x+b0)+ f(c).

Сравнивая коэффициенты при соответствующих степенях х, получаем:

an bn 1,

an 1 bn 2 cbn 1, an 2 bn 3 cbn 2 , …,

a1 b0 cb1, a0= f(c) сb0

Откуда

bn-1= an,

bn-2= an-1+с bn-1, bn-3= an-2+с bn-2,

…,

b1= a2+с b2, b0= a1+с b1, f(c)= a0+с b0.

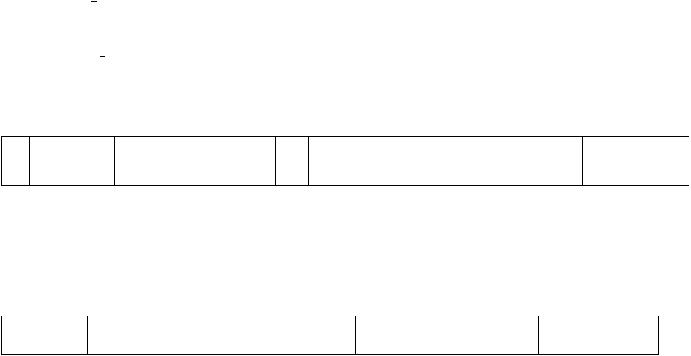
Для практического использования схему Горнера строят следующим образом:

an		an 1	…	ak	…	a1	a0
c bn 1 an	bn 2 an 1 cbn 1		… bk 1 cbk ak		…	b0 a1 cb1	f(c)= a0+с b0.
Отметим, что f(c) – это остаток при делении многочлена f(x) на x c
Пример.	Поделите с остатком f(x)= x5 4x3 +6 x2 8 x +10 на x 2. Найдите f(2)
	1	0	-4	6		-8	10
2	1	0 2 1 2	-4+4=0	6 0 2 6		-8+12=4 10 8 18 f (2)
Таким образом, частное q(x)= x4 +2x3 +6 x +4, остаток r =18,						f(2)=18.

Основная теорема алгебры

Теорема (основная теорема алгебры).

Всякий многочлен f (x) C[x],deg f (x) 1 имеет хотя бы один комплексный корень.

Первые попытки доказательства этой теоремы в XVII в. – Роте, Жирар, Декарт, в XVIII в. – Д’Аламбер, Эйлер, Лаплас, Лагранж. Первое строгое доказательство в 1799 г. – К.Гаусс. Доказательство см., например, Курош.

Следствие
f (x) C[x],deg f (x) 0,справедливо разложение
f (x) an(x с1)...(x сn),				( )
где an − старший коэффициент, с1,...,сn − корни многочлена					f (x).
Доказательство:
Пусть	f (x) a	n	xn ... a .	По основной теореме алгебры	корень с1		многочлена
		n	0
f (x); тогда по следствию из теоремы Безу справедливо представление						f (x) (x с1)q1(x),
где q1(x) имеет степень (n 1)				и по основной теореме алгебры		имеет	корень с2,
следовательно	f (x) (x c1)(x c2)q3(x), degq3(x) n 2, и т.д.

Витоге получаем выражение ( ), где коэффициент an нужен, т.к. коэффициент при xn должен быть an .

Объединяя одинаковые множители, разложение ( ) перепишем в виде:

f (x) a

с )k1...( x с

)kl ,

где

c1,...,cl

− попарно

различные корни

f(x), k1,...,kl

кратности

корней,

k1 ... kl

Следствие Каждый многочлен

f (x) C[x],deg f (x) n 1,

имеет n ровно корней,

если каждый корень считать столько раз, какова его кратность.

Формулы Виета

Теорема

(формулы

Виета).

Пусть

f (x) C[x],deg f (x) n 1, и

an=1.

f (x) xn a

xn 1

... a x a

, и c ,...,c − корни

f (x), причем каждый корень выписан

столько раз, какова его кратность

xn a

xn 1

... a x a

(x c ) ... (x c

an 1 (с1 с2 ... сn),

an 2

с1с2 с1с3 ... с1сn с2с3 ... сn 1сn,

an 3

(с1с2с3 ... с1с2сn ... сn 2сn 1сn),

...

( 1)n 1(c c ...c

c c

...c

n 2

... c

c ..c ),

1 2 n 1

1 2

2 3 n

( 1)nc ...c

Для доказательства

нужно

раскрывать скобки в правой части равенства

xn a

n 1

xn 1 ... a x a

(x c ) ... (x c

) и сравнивать коэффициенты при одинаковых

степенях х в левой и правой частях равенства.

При n=2,

f (x) x2

a x a

a1 (c1 c2),

a0 c1c2

n=3,

f (x) x3 a

x2 a x a

a2 (c1 c2 c3), a1 c1c2 c1c3 c2c3, a0 c1c2c3.

Многочлены с действительными коэффициентами

Пусть

f (x) a

xn a

n 1

xn 1 ... a

x a

C[x],

но a

Такой

многочлен

называется многочленом с действительными коэффициентами.

Теорема Если с C − корень многочлена

f (x)

с действительными коэффициентами,

то

C − также корень

f (x).

Доказательство:

Так как с C − корень многочлена f (x)

сn a

сn 1

... a с a

0. Возьмем

n 1

комплексное сопряжение обеих частей этого равенства.

По

свойствам

комплексно

сопряженных

чисел:

n ... a

сn a

сn 1

... a с a

сn ...

f (с)

n 1

n ... a

0 f (

) 0. Что и требовалось доказать.

Следствие Из теоремы если

многочлен

с действительными коэффициентами

имеет комплексный корень с, то f(x) x c

и f(x) x

f(x) (x с)(x

(x с)(x

) x2 (c

)x c

) R , c

R, (c

об

) p , c

Т.е. если многочлен с действительными коэффициентами имеет комплексный корень,

то он делится на многочлен вида x2 px qс отрицательным дискриминантом.

Неприводимые многочлены. Разложение многочленов на множители

Также как и целые числа можно разложить на простые множители, многочлены можно разложить в произведение неприводимых многочленов.

Определение Многочлен f (x) P[x],deg f (x) n 0, называется неприводимым над

множеством P=C R, если его нельзя представить в виде произведения многочленов из P[x],

степени которых меньше n и больше 0.

Неприводимыми многочленами над С являются многочлены вида x c и разложение многочлена f (x) С[x],deg f (x) n 0 на неприводимые многочлены имеет вид:

f (x) a

(x с )k1 ...( x с

)kl ,

где c1,...,cl − попарно различные корни f(x),

k1,...,kl

кратности корней.

Неприводимыми

многочленами

над

R являются

многочлены

вида x c,

c R и

x2 px q,

p,q R, p2 4q 0.

Разложение

многочлена

действительными

коэффициентами на неприводимые многочлены над R имеет вид:

f (x) a

(x с )k1...(x c )kl

(x2 p x q )m1

...(x2 p x q )mt ,

где c ,...,c , p ,..., p ,q ,...,q R,

0, j

. И k

... k

2(m

... m ) n.

1,t

t 1

Это разложение единственно с точностью до перестановки сомножителей.

Чтобы разложить данный многочлен на неприводимые множители над C, нужно решить квадратное уравнение x2 2x+2=0. Его корни x1,2 1 i.

Поэтому искомое разложение: f (x) (x 2)(x 1 i)2(x 1 i)2.

Соседние файлы в предмете Аналитическая геометрия и линейная алгебра

#
22.08.2023419.44 Кб2Лекция Алгебраические структуры 3 МО-1.pdf
#
22.08.2023396.51 Кб0Лекция Линейные отбражения 2 3.06.2020 МО-1.pdf
#
22.08.2023417.34 Кб0Лекция Линейные пространства 1 6.05.20 МО-1.pdf
#
22.08.2023357.98 Кб2Лекция Линейные пространства 2 13.05.20 МО-1.pdf
#
22.08.2023335.14 Кб0Лекция Линейные пространства 3 20.05.20 МО-1.pdf
#
22.08.2023971.57 Кб2Лекция Многочлены 2 МО-1.pdf
#
22.08.2023302.47 Кб0поверхность мо.docx
#
22.08.2023494.71 Кб2РГР 5Вариант.docx