24. Метод наименьших квадратов (расчёт коэффициентов)

На практике линия регрессии чаще всего ищется в виде линейной функции Y = b0 + b1X1 + b2X2 + ... + bNXN (линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых Y от их оценок (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):

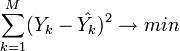
(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда Y = y(x1,x2,...xN).Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:

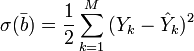
Условие минимума функции невязки:

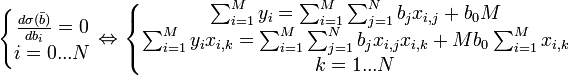
Полученная система является системой N + 1 линейных уравнений с N + 1 неизвестными b0...bN

Если представить свободные члены левой части уравнений матрицей

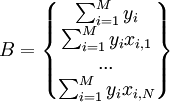
а коэффициенты при неизвестных в правой части матрицей

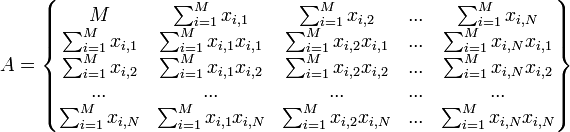
то получаем матричное уравнение: , которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии:

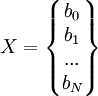
25. Регрессио́нный анализ (линейный) — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.

Типовые функции регрессии Mathcad. Для простых типовых формул аппроксимации предусмотрен ряд функций регрессии, в которых параметры функций подбираются программой Mathcad самостоятельно. К ним относятся следующие функции:

expfit(X,Y,S) – возвращает вектор, содержащий коэффициенты a, b и c экспоненциальной функции y(x) = a·exp(b·x)+c. В вектор S вводятся начальные значения коэффициентов a, b и c первого приближения. Для ориентировки по форме аппроксимационных функций и задания соответствующих начальных значений коэффициентов на рисунках слева приводится вид функций при постоянных значениях коэффициентов a и c.

lgsfit(X,Y,S) – то же, для выражения y(x) = a/(1+c·exp(b·x)).

pwrfit(X,Y,S) – то же, для выражения y(x) = a·x^b+c

sinfit(X,Y,S) – то же, для выражения y(x) = a·sin(x+b)+c. Подбирает коэффициенты для синусоидальной функции регрессии. Рисунок синусоиды общеизвестен.

logfit(X,Y) – то же, для выражения y(x)=a ln(x+b)+c. Задания начального приближения не требуется.

medfit(X,Y) – то же, для выражения y(x) = a+b·x, т.е. для функции линейной регрессии. Задания начального приближения также не требуется. График – прямая линия. Виды: Линейная регрессияПолиномиальная регрессия. Одномерная регрессия. Зональная регрессия.

Нелинейная регрессия