Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Магнитогорский государственный технический университет

им. Г.И. Носова»

Кафедра горных машин и транспортно-технологических комплексов

Расчёт показателей надёжности нерезервированных невосстанавливаемых систем

Сборник задач

для практических работ

по дисциплине

«Надёжность машин и механизмов»

для студентов направления

190100.68 Наземные транспортно-технологические комплексы

Магнитогорск 2014

Составитель: О.Р. Панфилова

Расчёт показателей надёжности нерезервированных невосстанавливаемых систем: сборник задач для практических работ по дисциплине «Надёжность машин и механизмов для студентов направления 190100.68 Наземные транспортно-технологические комплексы. Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2014. 16 с.

Предложены задачи по теме «Расчёт показателей надёжности нерезервированных невосстанавливаемых систем». Рассмотрен пример решения одной из задач. Даны краткие теоретические сведения, необходимые для решения задач.

Рецензент

© Панфилова О.Р.

СОДЕРЖАНИЕ

Введение

Учебный курс «Надёжность машин и механизмов» у студентов направления 190100.68 Наземные транспортно-технологические комплексы состоит из лекций и практических занятий.

Теория надежности как наука и техническая дисциплина имеет ряд особенностей:

- теория надежности – трудный для изучения предмет. Это объясняется широким использованием математики при изучении теории надежности, в частности таких дисциплин, как теория вероятностей и математическая статистика, решение интегральных, алгебраических и дифференциальных уравнений (с постоянными и переменными коэффициентами, линейных и нелинейных), математическая логика, теория систем массового обслуживания, элементы теории графов, методы статистического моделирования, методы оптимизации и многое другое;

- необходимость применения компьютерных технологий решения практических задач;

- случайный характер отказов и восстановлений;

- трудность математического моделирования объектов из-за отсутствия достоверных данных о надежности элементов системы, в частности, данных о законах распределения отказов и восстановлений;

- трудность, а во многих случаях невозможность статических испытаний из-за технических и экономических ограничений;

- сложность современных систем и, как результат, большие размерности уравнений, решение которых во многих случаях невозможно даже при использовании компьютерных технологий.

Сборник задач включает в себя не только задачи, но и краткие теоретические сведения, необходимые для их решения, а также пример решения типовой задачи.

1. Теоретические сведения

1. Методы расчёта показателей надёжности

Критериями надёжности невосстанавливаемых систем являются:

- P_c(t) – вероятность безотказной работы системы в течении времениt;

- Q_c(t) – вероятность отказа системы в течении времениt;

- T_c– среднее время безотказной работы системы;

- λ_с(t) – интенсивность отказов системы в моментt;

- f_c(t) – плотность распределения времени до отказа.

Между этими показателями существуют следующие зависимости:

,	(1)
,	(2)
,	(3)
,	(4)
.	(5)

Следует иметь в виду, что среднее время безотказной работы является неудовлетворительным показателем надёжности систем с коротким временем работы.

Нерезервированной называется такая система, в которой отказ любого элемента приводит отказу всей системы. При этом остальные элементы системы прекращают свою работу.

Показатели надёжности нерезервированной системы, состоящей из nэлементов, вычисляются по формулам:

,	(6)
,	(7)
,	(8)
,	(9)

где P_i(t) – вероятность безотказной работыi-го элемента,i= 1, 2, …,n;

f_i(t) – плотность распределения времени до отказаi-го элемента,i= 1, 2, …,n;

λ_i(t) – интенсивность отказовi-го элемента,i= 1, 2, …,n.

Существует другой способ вычисления плотности распределения времени до отказа системы, его рекомендуется использовать в качестве проверочного:

.

Среднее время безотказной работы системы также может быть определено по формуле Симпсона. Для системы из пяти элементов формула Симпсона принимает вид:

где n – число точек,

h – шаг интегрирования, выбираемый из условия обеспечения требуемой точности.

Для случая постоянных интенсивностей отказов элементов имеют место соотношения:

,	(10)
,	(11)
,	(12)
.	(13)
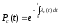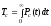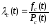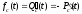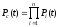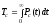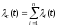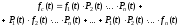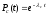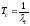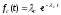