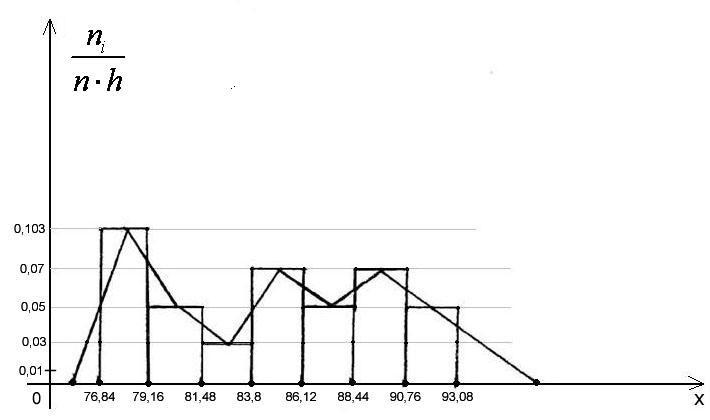
Гистограмма и полигон плотности относительных частот

f^*=-плотность относительных частот.

- длина соответствующего интервала

К=1+3,32ּlg(n) - количество классов (интервалов)

Плотность относительных частот f^* показывает, какая доля объектов совокупности приходится на единицу интервала.

Геометрическое представление эмпирической функции распределения F^*(x) называется кумулятой или кумулятивной кривой.

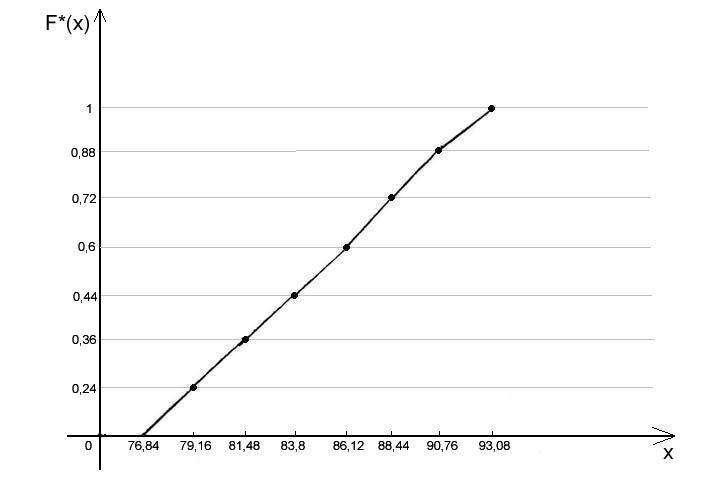
, где - накопленная абсолютная частота признака.

1.3. Числовые характеристики вариационного ряда

Для того, чтобы количественно охарактеризовать самые существенные свойства распределения, а также для того, чтобы можно было сравнить разные распределения, вычисляют средние показатели - выборочные числовые характеристики.

В статистике используются различные величины в зависимости от того, какие цели при анализе материала ставит исследователь. Понятием средней величины пользуемся в тех случаях, когда требуется определить средний надой по стаду, средний привес, средний прирост стада, средние клинические показатели деятельности сердца, лёгких, среднего состава крови и во многих других случаях.

Различают следующие виды средних величин: средняя арифметическая, средняя геометрическая, средняя квадратическая, средняя гармоническая, мода и медиана.

Наиболее распространенным видом средних величин является средняя арифметическая, которая бывает простой и взвешенной.

Возможны следующие случаи:

1. Результаты наблюдения не сведены в вариационный ряд или все частоты равны единице или одинаковы. Тогда вычисляют простую среднюю арифметическую

,

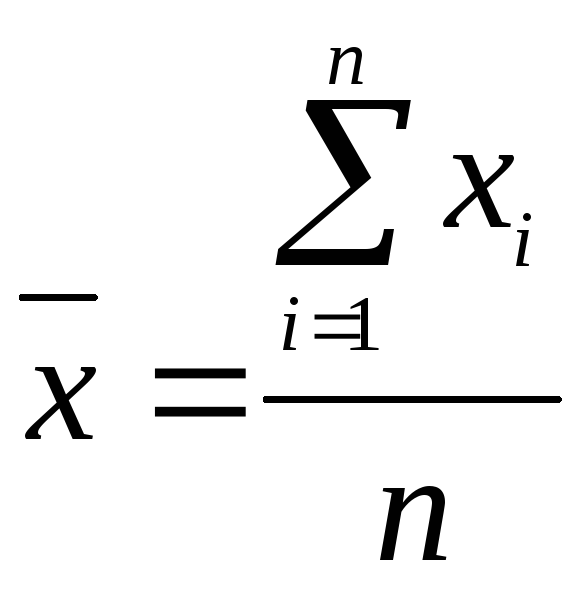где х_i – значение признака

n – объём результатов (число наблюдений).

2. Частоты n_i отличны друг от друга, то есть значения признака х_i повторяются. В этом случае вычисляют среднюю арифметическую взвешенную (выборочную среднею)

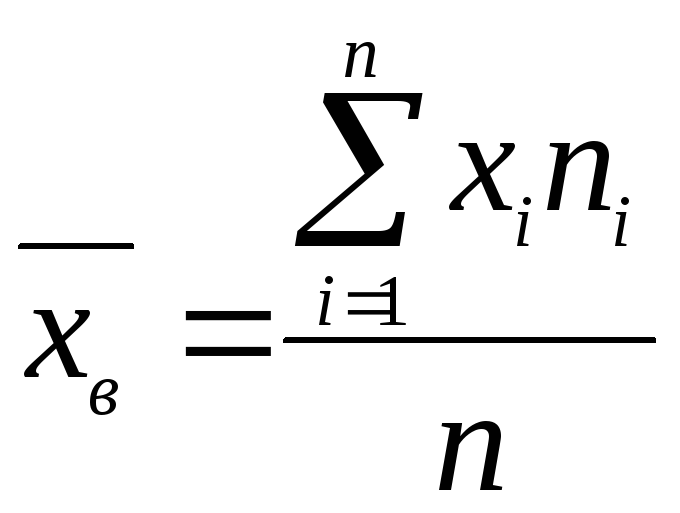
3. Распределение интервальное. В этом случае вместо х_i берут середину интервалов

Математические ожиданием (или средним значением) дискретной случайной величины Х, имеющий закон распределения, называется число, равное сумме произведений всех её значений на соответствующие им вероятности.

Обозначаются М(Х)

Дисперсия характеризует рассеяние значений признака относительно выборочной средней .

Выборочная дисперсия – это среднее арифметическое значение квадратов отклонения признака от выборочной средней.

Для её вычисления применяют формулу

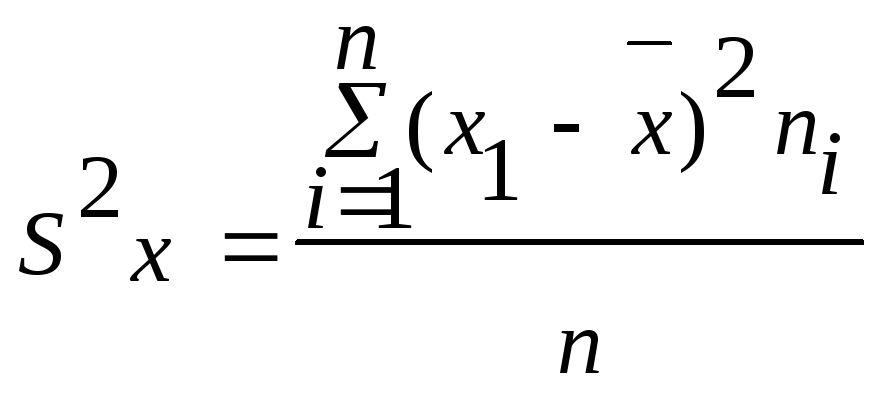
В случае, если общее число вариант мало (n<30), лучше применять формулу

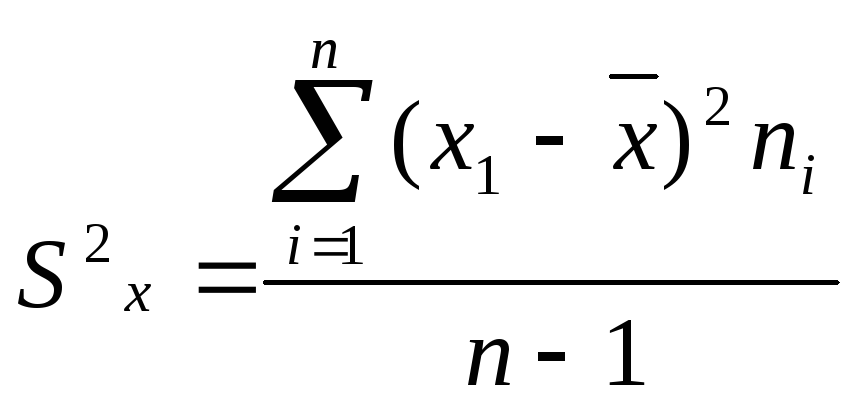
Выборочное среднее квадратичное отклонение S_x находят по формуле

,

а исправленное выборочное среднее квадратичное отклонение S по формуле

Коэффициент вариации V – это выборочное процентное отношение выборочного среднего квадратичного отклонения к выборочной средней

Коэффициент вариации показывает изменчивость признака.

Если С_v > 20% -изменчивость значительная; если 10% < C_v < 20%- средняя; если C_v < 10%- незначительная.

Коэффициент вариации позволяет сравнивать изменчивость признаков, имеющих разные единицы измерения.

В качестве описательных характеристик вариационного ряда используется медиана, мода, размах вариации (выборки) и т.д.

Размахом вариации называется число

R=X_max - X_min, где

Х_max-наибольший, X_min-наименьший вариант ряда.

Медиана – это значение варианта, который делит ранжированный ряд на равные по числу вариант части.

4 7 12 8 9 5 7 13 15

Ме = 12 Ме =

Если признак Хпредставлен интервально:

медианному интервалу соответствует первая накопленная частота превосходящая n/2.

,

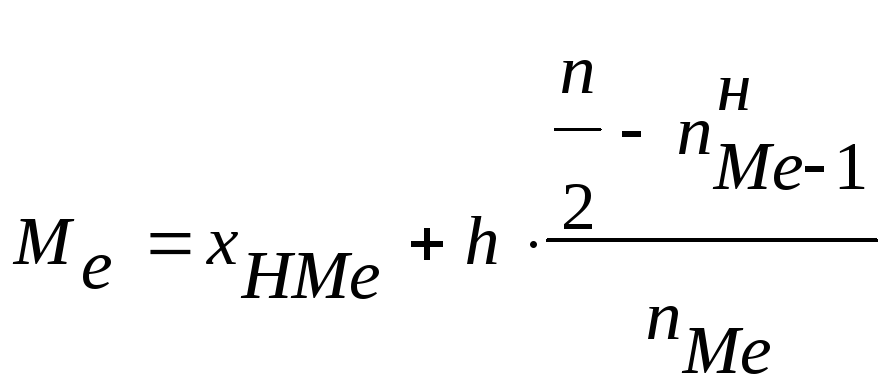где - нижняя граница медианного интервала

–шаг разбиения, ширина класса

–накопленная частота интервала, предшествующего медианному интервалу

- абсолютная частота медианного интервала.

Модой называется вариант, имеющий наибольшую частоту.

Класс с наибольшей частотой называется модальным.

Для определения моды интервальных рядов служит формула

,

где - нижняя граница модального интервала

–ширина класса

–абсолютная частота модального интервала

–абсолютная частота интервала предшествующего модальному

–абсолютная частота интервала следующего за модальным.

При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. Вводят специальные характеристики: асимметрию и эксцесс.

Для нормального распределения эти характеристики равны нулю.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадрата отклонения.

Центральным моментом порядка k случайной величины X называется математическим ожиданием величины (X – M(X))^k, обозначается через μ_k.

Таким образом, по определению

μ_k = M(X – M(X))^k.

В частности, μ₂ = D(X), то есть центральный момент 2-го порядка есть дисперсия

μ₁ = M(X – M(X)) = 0

Для дискретной случайной величины

Среди моментов высших порядков особое значение имеют центральные моменты 3-го и 4-го порядков, называемых соответственно коэффициентами асимметрии и эксцесса.

Коэффициентом асимметрии ("скошенности") А случайной величины X называется величина

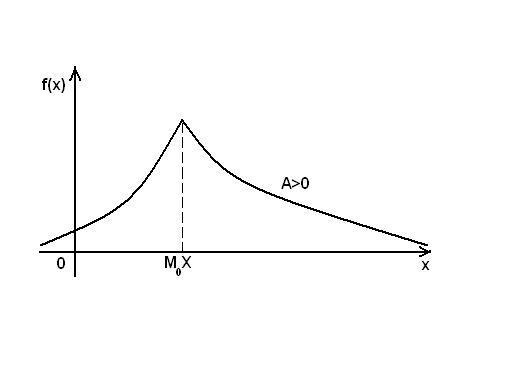
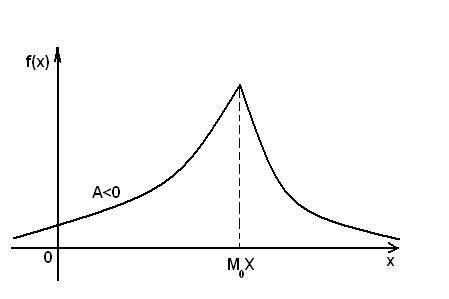
Если А > 0, то кривая распределения более полога справа от М₀(X);

если А < 0, то кривая распределения более полога слева от М₀(X).

Коэффициентом эксцесса ("островершинности") Е случайной величины X называется величина

Величина Е характеризует островершинность или плосковершинность распределения.

Для нормального закона распределения А = 0 и Е = 0; остальные распределения сравниваются с нормальным: если

Е > 0 – более островершинные, а распределения "плосковершинные" имеют Е < 0