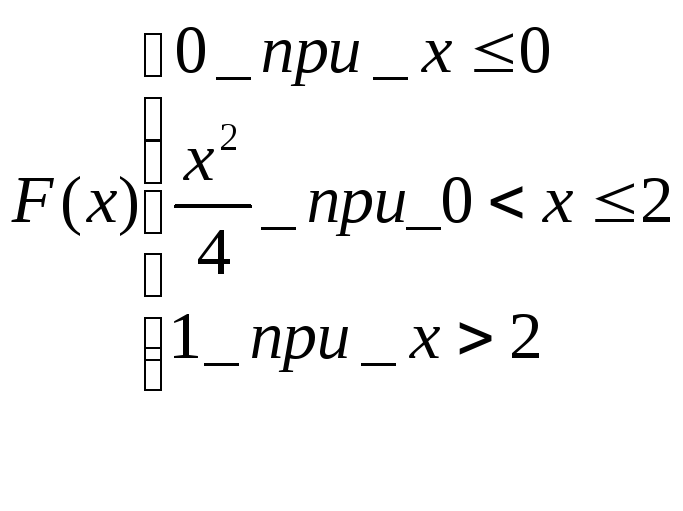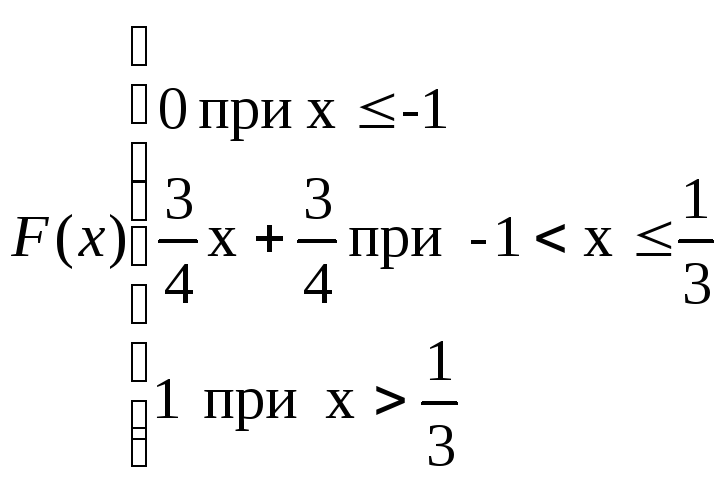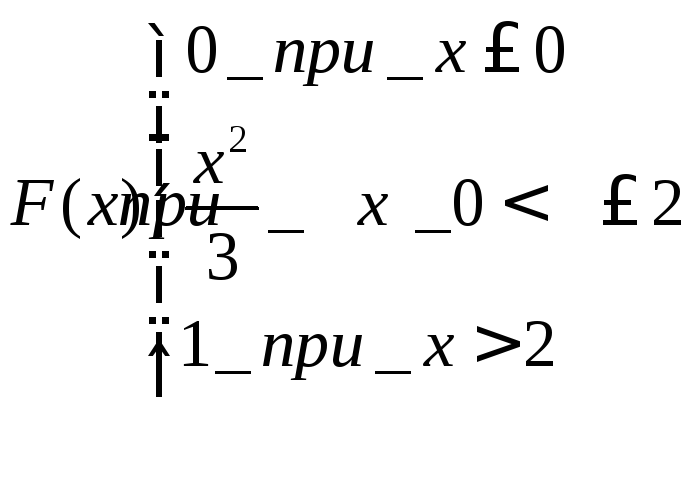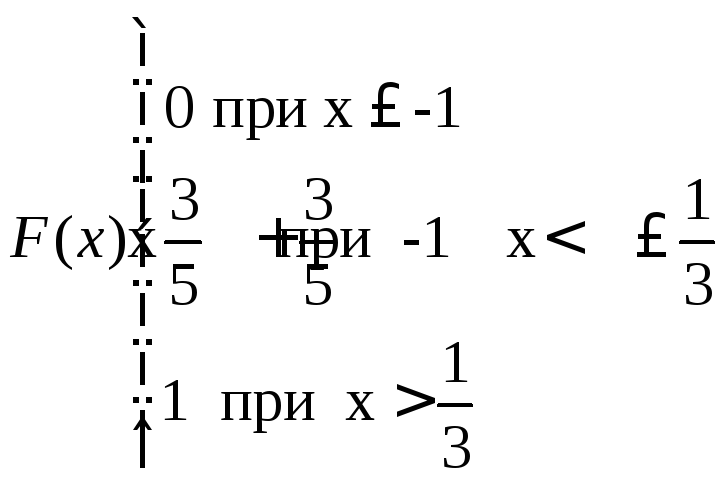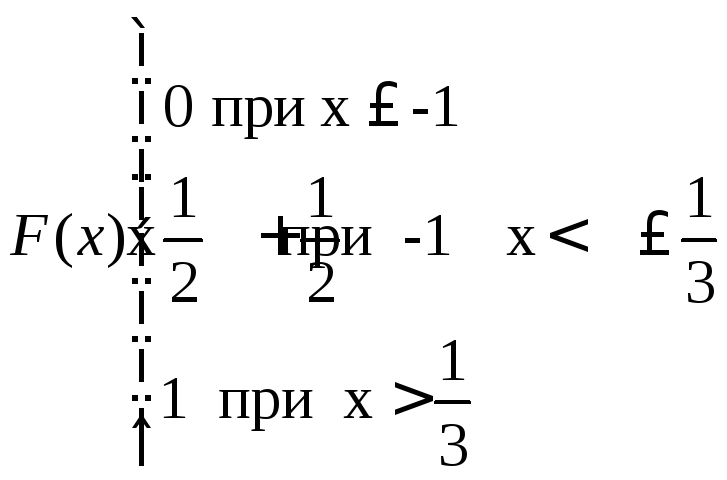- •Методические указания
- •Для решения контрольной и самостоятельной работы
- •По разделу математики
- •«Элементы теории вероятностей и математической статистики»
- •I. Элементы теории вероятностей
- •1.1. Случайные величины. Вероятность случайного события
- •1.2.Теоремы сложения, умножения вероятностей
- •1.3 .Формула полной вероятности. Формула Бейеса
- •Формула Бейеса. (формула гипотез)
- •1.4. Закон распределения дискретной случайной величины
- •Формула Пуассона
- •Локальная формула Муавра-Лапласа
- •Интегральная форма Лапласа
- •1.5. Интегральная функция распределения
- •1.6. Дифференциальная функция распределения
- •1.7. Равномерное распределение непрерывной случайной величины
- •1.8.Числовые характеристики случайных величин
- •1.7. Нормальный закон распределения вероятностей непрерывной случайной величины
- •2.Элементы математической статистики
- •I. Выборки и их характеристики
- •1.1. Выборочный метод и способы составления выборок
- •1.2. Статистическое распределение и его геометрическое изображение
- •Алгоритм составления дискретного статистического распределения:
- •Гистограмма и полигон плотности относительных частот
- •1.3. Числовые характеристики вариационного ряда
- •1.4.Статистические оценки параметров распределения. Доверительные интервалы
- •1.5. Статистическая проверка статистических гипотез
- •II Элементы корреляционного анализа
- •2.1. Статистическая зависимость случайных величин. Уравнения регрессии.
- •2.2. Корреляционная зависимость. Коэффициент корреляции.
- •1) Метод квадратов
- •2) Ранговый метод
- •2.3. Проверка гипотезы о значимости выборочного
- •Разбор типовых задач Тема: Формула вероятности события
- •Тема: формула полной вероятности
- •Тема :случайная величина и ее числовые характеристики числовые характеристики дискретных случайных величин
- •Числовые характеристики непрерывных случайных величин
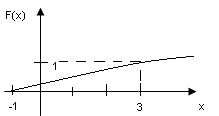
- •Тема:Функции распеределения
- •Тема: Элементы статистической обработки данных
- •Тема :понятие о корреляционной зависимости
- •Вопросы для самопроверки Основные понятия теории вероятностей. Теоремы сложения и умножения вероятностей.
- •Повторные независимые испытания
- •Случайная величина и ее числовые характеристики
- •Основные сведения из математической статистики Вопросы для самопроверки
- •Понятие о корреляционной зависимости Вопросы для самопроверки
- •Статистические оценки параметров распределения
- •Вопросы для самопроверки
- •Задания для самостоятельной работы по теме «Элементы теории вероятностей и математической статистики »
- •Задания для контрольной работы по теме «Элементы теории вероятностей и математической статистики»
- •Контрольная работа «Статистическое оценивание данных»
- •Вариант – 1
- •Стандартные коэффициенты корреляции, которые считаются достоверными (по л.С. Каминскому)
- •Литература
Задания для контрольной работы по теме «Элементы теории вероятностей и математической статистики»
|
Контрольная работа «Элементы теории вероятностей» Вариант – 1 1. В пенале 14 карандашей, из них 6 цветных. Наугад достали 4 карандаша. Найти вероятность того, то среди них нет цветных. 2. В ящик, содержащий 4 шара, добавили 4 белых шара, после чего из него наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. Три лампочки включены последовательно в цепь. Вероятность перегорания любой из них равна 0,5. Найти вероятность того, что при повышенном напряжении тока в цепи не будет. 4. Дискретная случайная величина задана законом распределения вероятностей:
Найти дисперсию случайной величины 3Х.
|
Контрольная работа №6 «Элементы теории вероятностей» Вариант – 2 1. В конверте 10 фотокарточек, среди них 6 нужных. Наугад достали 4 фотокарточки. Найти вероятность того, что среди них 3 нужных. 2. В ящик, содержащий 2 шара, добавили 6 белых шаров, после чего из него наудачу извлечен один шар. Найти вероятность того что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. Вероятность одного попадания в цель при залпе из 2-х орудий равна 0,44. Найти вероятность поражения цели при одном выстреле 1-ым орудием, если для 2-го эта вероятность равна 0,8. 4. Дискретная случайная величина задана законом распределения вероятностей:
Найти a и b, если ее математическое ожидание равно 3,3.
Чему равна вероятность Р(0,5<Х<1) | ||||||||||||||||||
|
Контрольная работа №6 «Элементы теории вероятностей» Вариант – 3 1. В ящике 12 мышей, среди них 4 белых. Наугад достали 4 мыши. Найти вероятность того, что все они белые. 2. В ящик, содержащий 3 шара, добавили 3 белых шара, после чего из него наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. Вероятность хотя бы одного попадания стрелком в мишень при 3-х выстрелах равна 0,875. Найти вероятность попадания при одном выстреле. 4. Дискретная случайная величина Х задана законом распределения вероятностей:
Найти математическое ожидание случайной величины Y=2X.
Найти вероятность того, что в результате величина Х примет значение, заключенное в интервале (0;1/3) |
Контрольная работа №6 «Элементы теории вероятностей» Вариант – 4 1. На клумбе растут 20 астр, из них 6 белых. Наугад сорвали 4 астры. Найти вероятность того, что среди сорванных астр 2 белые. 2. В ящик, содержащий 2 шара, добавили 2 белых шара, после чего из него наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. Вероятность поражения цели при выстреле из одного орудия равна 0,7. Найти вероятность поражения цели при залпе из 3-х орудий. 4. Дискретная случайная величина задана законом распределения вероятностей:
Найдите a и b, если ее математическое ожидание равно 2,5.
Найти математическое ожидание Х. |
|
Контрольная работа «Элементы теории вероятностей» Вариант №5 1. У кошки 8 котят, среди них 4 белых. Наугад взяли 4 котят. Найти вероятность того, что все они белые. 2. В ящик, содержащий 5 шаров, добавили 2 белых шара, после чего из него наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:
4. Вероятность хотя бы одного попадания стрелком в мишень при 3-х выстрелах равна 0,875. Найти вероятность попадания при одном выстреле. 5. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 8 и 2. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (12;14).
|
Контрольная работа №6 «Элементы теории вероятностей» Вариант –6 1. в пакете 16 конфет, среди них 6 шоколадных. Наугад достали 4 конфеты. Найти вероятность того, что среди них 3 шоколадные. 2. В ящик, содержащий 2 шара, добавили 7 белых шаров, после чего из него наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. Вероятность хотя бы одного попадания стрелком в мишень при 3-х выстрелах равна 0,875. Найти вероятность попадания при одном выстреле. 4. Дискретная случайная величина задана законом распределения вероятностей:
Найти a и b, если ее математическое ожидание равно 3,3.
Чему равна вероятность Р(0,5<Х<1) | ||||||||||||||||||
|
Контрольная работа №6 «Элементы теории вероятностей» Вариант – 7 1 в корзине 14 яблок, среди них 4 красных. Наугад достали 4 яблока. Найти вероятность того, что все они красные. 2. В ящик, содержащий 3 шара, добавили 5 белых шаров, после чего из него наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. 3 лампочки включены последовательно в цепь. Вероятность перегорания любой из них равна 0,5. Найти вероятность то, что при повышенном напряжении тока в цепи не будет. 4. Дискретная случайная величина Х задана законом распределения вероятностей:
Найти математическое ожидание случайной величины Y=2X.
Найти вероятность того, что в результате величина Х примет значение, заключенное в интервале (0;1/3) |
Контрольная работа №6 «Элементы теории вероятностей» Вариант – 8 1. В группе 15 студентов, среди них 5 отличников. Наугад отобрано 4 студента. Найти вероятность того, что среди них 2 отличника. 2. В ящик, содержащий 2 шара, добавили 4 белых шара, после чего наугад достали 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. Вероятность поражения цели при выстреле из одного орудия равна 0,7. Найти вероятность поражения цели при залпе из 3-х орудий. 4. Дискретная случайная величина задана законом распределения вероятностей:
Найдите a и b, если ее математическое ожидание равно 2,5.
Найти математическое ожидание Х. |
|
Контрольная работа №6 «Элементы теории вероятностей» Вариант – 9 1 В конверте 9 лотерейных билетов, среди них 6 выигрышных. Наугад достали 3 билета. Найти вероятность того, что все они выигрышные. 2. В ящик, содержащий 3 шара, добавили 6 белых шаров, после чего из него наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. Вероятность поражения цели при выстреле из одного орудия равна 0,7. Найти вероятность поражения цели при залпе из 3-х орудий. 4. Дискретная случайная величина Х задана законом распределения вероятностей:
Найти математическое ожидание случайной величины Y=2X.
Найти вероятность того, что в результате величина Х примет значение, заключенное в интервале (0;1/3) |
Контрольная работа №6 «Элементы теории вероятностей» Вариант – 10 1. В корзине 17 грибов, среди них 10 белых. Наугад достали 4 гриба. Найти вероятность того, что все они белые. 2. В ящик, содержащий 5 шаров добавили 3 белых шара, после чего из него наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету. 3. 3 лампочки включены последовательно в цепь. Вероятность перегорания любой из них равна 0,5. Найти вероятность то, что при повышенном напряжении тока в цепи не будет. 4. Дискретная случайная величина задана законом распределения вероятностей:
Найдите a и b, если ее математическое ожидание равно 1,5.
Найти математическое ожидание Х. |