Основные сведения из математической статистики Вопросы для самопроверки

1. Что понимается под генеральной совокупностью?

2. Что такое выборка, объем выборки? Как обеспечивает­ся представительность выборки?

3. Как получают повторную и бесповторную выборки?

4. Перечислите способы отбора статистического материа­ла.

5. Что такое частота появления варианты в выборке?

6. Как получают относительную частоту варианты в вы­борке?

7. Как получают вариационный ряд распределения?

8. Как графически изображают вариационные ряды?

9. Как построить многоугольник распределения относи­тельных частот?

10.Как построить гистограмму распределения плотностей относительных частот?

11.Дайте определение моды и медианы выборки.

Понятие о корреляционной зависимости Вопросы для самопроверки

1. 1.В чем состоит различие между функциональной и ста­тистической зависимостью между случайными величинами?

2. Опишите форму корреляционной таблицы.

3. В чем состоят две основные задачи корреляционного анализа?

4. Какую корреляционную зависимость называют линей­ной?

5. Запишите выборочные уравнения прямых регрессии. Дайте определение выборочного коэффициента корреля­ции и перечислите его основные свойства.

6. Что следует сказать о зависимости двух случайных ве­личин, если коэффициент корреляции равен нулю? Если коэффициент корреляции ранен единице? Если коэффициент корреляции ранен минус единице?

7. В чем суть метода наименьших квадратов для опреде­ления параметров линии регрессии?

Статистические оценки параметров распределения

1. Вопросы для самопроверки

2. В чем сущность задачи по определению параметров генеральной совокупности? В чем особенность этой задачи?

3. Как вычисляется средняя арифметическая выборки при малых и больших ее объемах?

4. Как вычисляется дисперсия выборки в случаях малого и большого ее объемов?

5. Какую величину принимают за среднюю генеральной совокупности?

6. Какую величину принимают за дисперсию генеральной совокупности?

7. Что понимают под доверительным интервалом и дове­рительной вероятностью?

8. Как вычисляют среднее квадратическое отклонение средней выборки?

9. Какова вероятность попадания генеральной средней в интервал размером ±2 (±3) средних квадратических откло­нения средней выборки при нормальном распределении?

10. Если доверительная вероятность будет увеличена, то как изменится доверительный интервал при других равных условиях?

11. Что надо сделать с объемом выборки, чтобы умень­шить доверительный интервал при том же значении довери­тельной вероятности?

Задания для самостоятельной работы по теме «Элементы теории вероятностей и математической статистики »

I

1. В одной из групп 2/3 студентов занимаются на хорошо и отлично. Определить вероятность того, что из пяти наугад взятых студентов на хорошо и отлично учатся: а) два студента; б) не более двух студентов.

2. В некоторых условиях вероятность своевременного прибытия поезда на станцию равна 0,8. Какова вероятность того, что из четырех ожидаемых поездов своевременно прибудут: а) два поезда; б) не менее двух поездов?

3. Вероятность попадания в цель при каждом выстреле в некоторых условиях равна 0,4. Найти вероятность того, что при пяти выстрелах: а) не будет ни одного попадания; б) будет не менее трех попаданий.

4. Всхожесть семян данного сорта растений оценивается вероятностью 0,6. Найти вероятность того, что из шести посеянных семян взойдут: а) пять семян; б) не более двух семян.

5. Вероятность выполнения плана каждым из пяти независимых между собой хозяйств равна 0,5. Найти вероятность того, что план выполнят: а) пять хозяйств; б) не менее трех хозяйств.

6-10. Школьники посадили на школьном участке n деревьев. Вероятность того, что каждое дерево приживется, равна p. Найти вероятность того, что приживется m деревьев. Данные приведены в таблице.

Номера задач	6	7	8	9	10
n p m	600 0,4 210	400 0,9 348	225 0,8 171	400 0,5 178	196 0,5 84

II

1-5. Птицеферма отправила на базу n штук яиц. Вероятность того, что каждое яйцо повредится в пути, равна p. Найти вероятность того, что на базу прибудут m непригодных яиц. Данные приведены в таблице.

Номера задач	1	2	3	4	5
n p m	5000 0,0002 2	1000 0002 3	2500 0,0004 3	4000 0,00025 1	10000 0,0004 3

6-10. На опытной станции посажено n семян кукурузы. Всхожесть семян равна p. Найти вероятность того, что из посеянных семян число взошедших от до. Данные приведены в таблице.

Номера задач	6	7	8	9	10
n p	600 0,6 348 372	400 0,8 328 344	450 2/3 280 320	100 0,8 78 90	600 0,4 210 270

Ш

2. Найти интегральную функцию распределения случайной величины Х, заданной рядом распределения:

Х	1	2	3
Р	0,3	0,2	0,5

и построить ее график. 2. Средняя продолжительность срока реализации товара (в часах) имеет следующую плотность распределения:      φ(х)=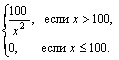Вычислить:      а) вероятность того, что товар будет реализован позднее 150 часов;      б) вероятность того, что товар будет реализован позднее 200 часов и в то же время не позднее 300 часов. 3.Дискретная случайная величинаХ, имеющая смысл числа курьеров, задействованных для доставки корреспонденции в коммерческой организации, задана законом распределения:     

Х	0	1	2	3
Р	0,4	0,1	0,3	0,2

Найти математическое ожидание, дисперсию, среднее квадратическое отклонение. 4 . Непрерывная случайная величина Х задана функцией распределения 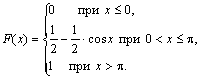     Найти математическое ожидание и дисперсию этой случайной величины.

5. Дана функция распределения непрерывной случайной величины Х

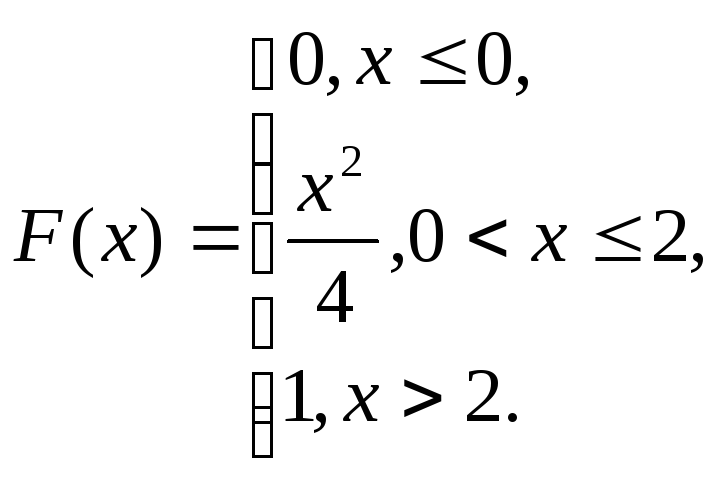
Требуется найти:

1. график F(x),

2. плотность f(x),

3. график f(x),

4. математическое ожидание М(Х),

5. дисперсию D(Х),

6. среднее квадратическое отклонение σ,

7. Р(Х < –2), P( 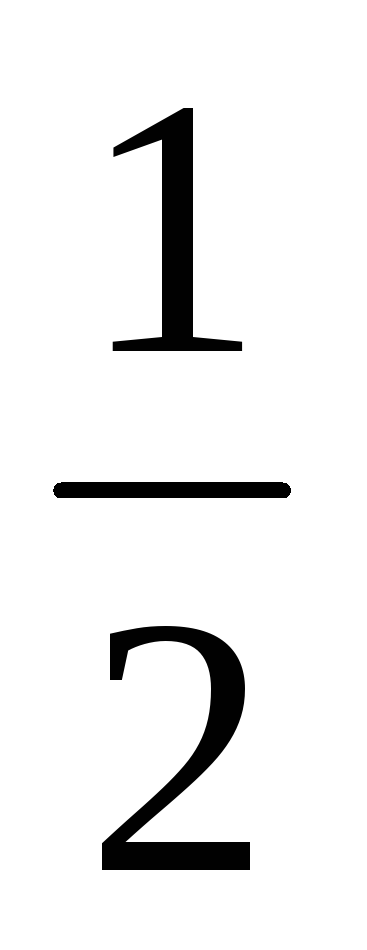≤ Х < 1) P(Х ≥ ).

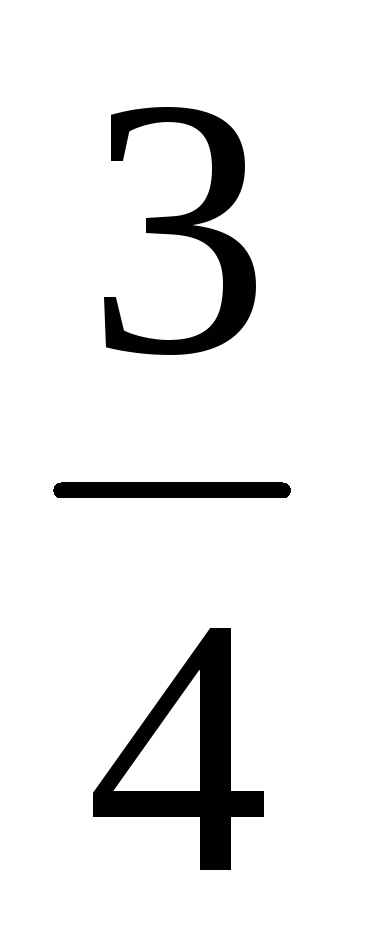6. Случайная величина  — число очков, выпадающих при однократном бросании игральной кости. Возможные значения  — числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что  примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения ?

7. Пусть случайная величина  подчиняется нормальному закону распределения вероятностей с параметрами a=0, =2.     Определить:        1) ;        2) ; 

8. В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы 

 .

9.Дискретная случайная величина Х задана законом распределения:

Х	1	3	6	8
Р	0,2	0,1	0,4	0,3

Построить многоугольник распределения.

10. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:

Х	–5	2	3	4
Р	0,4	0,3	0,1	0,2

IV

В задачах 1-10 заданы математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти: а) вероятность того, что Х примет значение, принадлежащее интервалу (α;β); б) вероятность того, что абсолютная величина отклонения Х- а окажется меньше ɛ.

1. а=15 σ=2 α=9 β=19 ɛ=3

2. а=14 σ=4 α=10 β=20 ɛ=4

3. а=13 σ=4 α=11 β=21 ɛ=8

4. а=18 σ=5 α=8 β=23 ɛ=10

5. а=12 σ=5 α=12 β=22 ɛ=5

6. а=11 σ=4 α=15 β=19 ɛ=6

7. а=10 σ=8 α=14 β=18 ɛ=2

8. а=9 σ=2 α=7 β=15 ɛ=3

9. а=8 σ=4 α=8 β=12 ɛ=8

10. а=16 σ=5 α=11 β=21 ɛ=4

V

В задачах 31-40 вычислить выборочный коэффициент корреляции двух случайных величин Х и У и найти выборочное уравнение прямой регрессии У на Х. Данные взять из таблицы.

31		32		33		34		35		36		37		38			39		40
х	у	х	у	х	у	х	у	х	у	х	у	х	у	х		у	х	у	х	у
28 27 28 27 29 26 28 28 29 30	29 29 28 28 29 28 32 30 28 29	24 25 23 24 20 24 23 21 23 23	18 19 18 19 20 19 19 21 19 18	24 25 21 23 20 23 24 24 23 23	20 21 19 19 19 18 19 18 19 18	47 49 43 46 41 46 49 48 45 46	40 42 38 38 37 36 39 35 37 38	18 16 17 20 20 20 21 22 23 23	22 23 21 27 26 28 32 32 32 37	28 16 32 20 24 24 28 36 12 20	15 22 15 21 22 18 17 14 25 21	33 30 24 12 30 33 21 24 18 15	36 32 24 12 36 28 24 20 16 12	24 25 21 23 23 20 24 24 23 23	15 14 22 21 18 25 15 21 17 22		34 35 31 27 23 19 15 11 8 7	13 13 18 23 25 30 33 35 37 33	22 23 24 25 25 23 18 21 19 20	25 30 30 30 35 25 25 20 20 20