Тема: Элементы статистической обработки данных

Задача1.Для определения средней живой массы трехмесячного теленка определенной породы были взвешены 100 животных и результаты сведены в таблицу

Масса, кг	23-25	25-27	27-29	29-31	31-33	33-35	35-37
Число телят, гол	3	10	6	16	15	30	20

Найти:

1. Величины, которые следует принять за среднюю массу и среднее квадратическое отклонение.

2. Ошибку средней и коэффициент вариаций.

3. Доверительный интервал, в котором с вероятностью 0,95 заключена средняя масса.

Решение:

1. В качестве приближенного значения средней массы принимаем выборочную среднюю, а за значение признака – середины интервалов

Вычисляем выборочную исправленную дисперсию

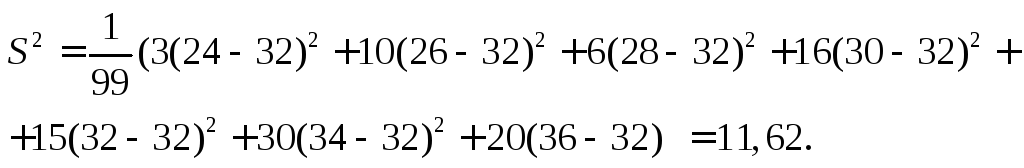
Находим исправленное выборочное среднее квадратичное отклонение

2. Ошибка средней равна

Коэффициент вариации

показывает, что изменчивость признака средняя.

3. Поскольку n = 100 > 30 и у нас случай нормального распределения, то доверительный интервал находим по формуле

Из условия 2Φ(t_γ) = 0,95 определяем Φ(t_γ) = 0,475,

а по таблице приложений находим t_γ = 1,96.

Поэтому

или 31,32 < x < 32,68 кг – доверительный интервал для заданной вероятности.

Задача 2.Из предварительных оценок известны значения

а)оценить объем необходимой выборки, чтобы точность оценки равнялась

б)оценить объем необходимой выборки, чтобы точность оценки равнялась

Решение.

а)Известно,что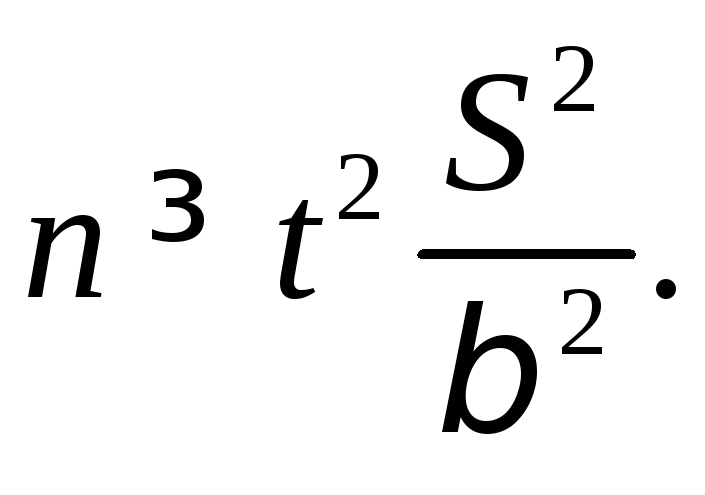По условиюзначениеt найдем по приложению 2:

Тогда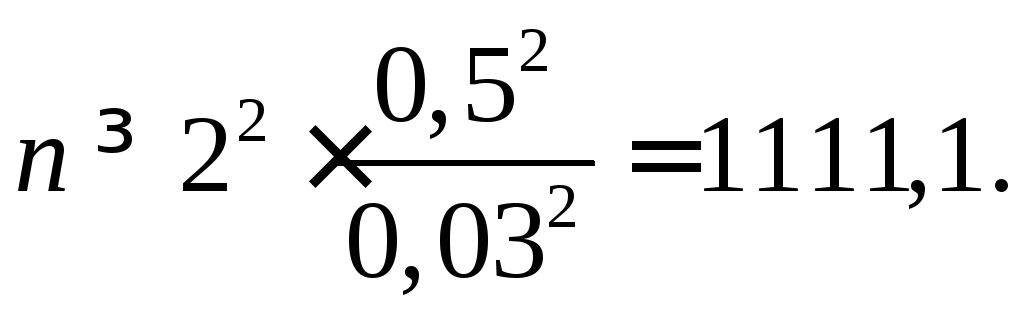

Следовательно, для заданной доверительной вероятности и точности оценки объем выборки должен составлять не менее 1112.

б)ДаноПо приложению 4 руководства В.Е.Гмурмана находим значенияблизкие к 0,10, их два:

и

Следовательно

Ответ:1112;

Задача 3.При использовании определенных методов лечения среди 100 больных было 25 выздоровевших.Определить пределы, в которых с заданной довернительной вероятностью лежит вероятность выздоровления

Решение: Известно, что

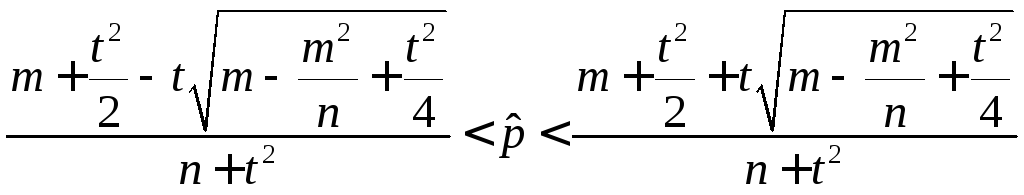
найдем по приложению 3 руководства В.Е. Гмурмана:

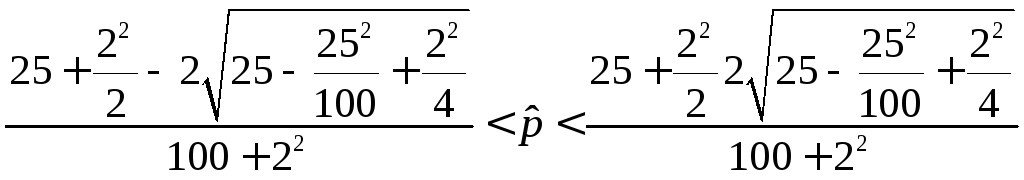
Или

Ответ:

Тема :понятие о корреляционной зависимости

Задание 1. Вычислить коэффициент корреляции, определить направление и силу связи между количеством кальция в воде и жесткостью воды, если известны следующие данные (табл. 1). Оценить достоверность связи. Сделать вывод.

Таблица 1

Жесткость воды (в градусах)	Количество кальция в воде (в мг/л)
4 8 11 27 34 37	28 56 77 191 241 262

Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант.

Решение: Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).

Жесткость воды (в градусах) X1	Количество кальция в воде (в мг/л) Y1	dх	dу	dх х dу (х1-)(у1—)	dx2 (х1 — )2	dy2 (у1— )2
4 8 11 27 34 37	28 56 77 191 241 262	-16 -12 -9 +7 +14 +16	-114 -86 -66 +48 +98 +120	1824 1032 594 336 1372 1920	256 144 81 49 196 256	12996 7396 4356 2304 9604 14400
Мх=Σ х / n	Му=Σ у / n			Σ dх x dу=7078	Σ dх2=982	Σ dy2=51056
=120/6=20	=852/6=142

1. Определить средние величины M_x ряду вариант "х₁" и М_у в ряду вариант "у₁" по формулам: М_х = Σх/n (графа 1) и М_у = Σу/n (графа 2)

2. Найти отклонение (d_х и d_у) каждой варианты от величины вычисленной средней в ряду "x" и в ряду "у" d_х = х — М_х (графа 3) и d_y = у — М_у (графа4).

3. Найти произведение отклонений d_x х d_y и суммировать их: Σ d_х х d_у (графа 5)

4. Каждое отклонение d_x и d_у возвести в квадрат и суммировать их значения по ряду "х" и по ряду "у": Σ d_x² = 982 (графа 6) и Σ d_y² = 51056 (графа 7).

5. Определить произведение Σ d_x² х Σ d_y² и из этого произведения извлечь квадратный корень

6. Полученные величины Σ (d_x x d_y) и √(Σd_x² x Σd_y²) подставляем в формулу расчета коэффициента корреляции:

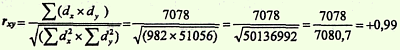
7. Определить достоверность коэффициента корреляции: 1-й способ. Найти ошибку коэффициента корреляции (mr_xy) и критерий t по формулам:

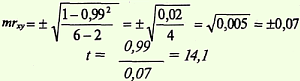
Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.

2-й способ. Достоверность коэффициента корреляции оценивается по таблице "Стандартные коэффициенты корреляции" (см. приложение 1). При числе степеней свободы (n — 2)=6 - 2=4, наш расчетный коэффициент корреляции r_xу = + 0,99 больше табличного (r_табл = + 0,917 при р = 99%).

Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная: r_ху = + 0,99, р > 99,9%).

Задание1. Вычислить выборочный коэффициент кор­реляции двух случайных величин х и у и найти выборочное уравнение прямой регрессии у на х по данным таблицы:

х	20	19	18	21	23	22	23	24	25	25
у	20	20	20	26	25	25	30	30	30	35

Решение. Вычислим выборочный коэффициент корреляции по формуле:

r= 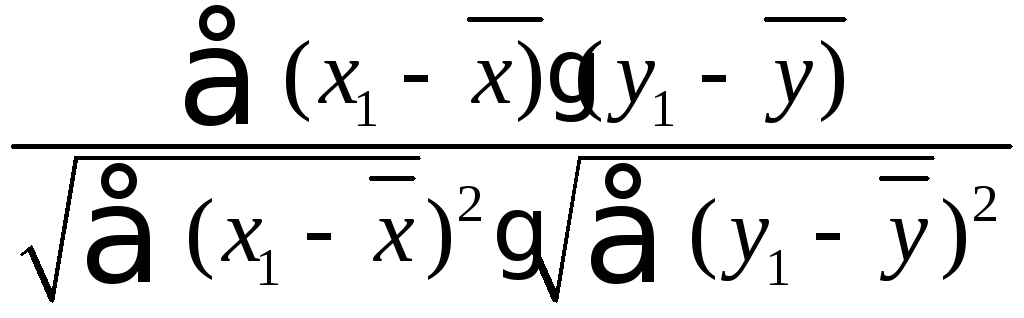(1)

Для вычисления величин, входящих в формулу, составим вспомогательную таблицу. П этой таблице результаты наблю­дений х₁ и у₁ записаны столбцами. Внизу каждого столбца вычислены суммы для расчета средних и . Правее распо­ложены столбцы, в которых вычислены разности х₁ — н у₁— , их квадраты и произведения. Соответственно суммируют­ся значения столбцов, чтобы получить величины для подста­новки в формулу (1).Среднее = = 22; = = 26.

х1	у1	х1 —	(х1 — )2	у1—	(у1— )2	(х1—)(у1—)
20 19 18 21 23 22 23 24 25 25	20 20 20 25 25 25 30 30 30 35	-2 -3 -4 -1 1 0 1 2 3 3	4 9 16 1 1 0 1 4 9 9	-6 -6 -6 -1 -1 -1 4 4 4 9	36 36 36 1 1 1 16 16 16 81	12 18 24 1 -1 0 4 8 12 27
220	260	0	54	0	240	105

Из таблицы имеем

Σ (х₁ — ) (у₁— )= 105, Σ (х₁ — )²= 54, Σ (у₁— )²= 240.

Подставляя эти значения в формулу (I), получим

r=≈ 0,92.

Выборочное уравнение прямой регрессии у на х имеет вид

𝑦- = r (2)

За приближенные значения величин σ_х и σ_у принимают соот­ветственно

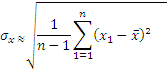
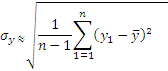
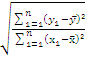= = ≈ 2,11.

Подставляя в формулу (2) =22; = 26; r=0,92;

= 2,11 , получим

у—26=0,92 · 2,11(х—22)

или у = 1,94х —16,68 - это и есть искомое выборочное урав­нение прямой регрессии у на х.