Пример 1: Описательные статистики и критерий Стьюдента

В ходе рассмотрения примера мы будем использовать вымышленные сведения, чтобы читатель мог провести необходимые преобразования самостоятельно.

Так, допустим, в ходе исследований изучали влияние препарата А на содержание вещества В (в ммоль/г) в ткани С и концентрацию вещества D в крови (в ммоль/л) у пациентов, разделенных по какому-то признаку Е на 3 группы равного объема (n = 10). Результаты такого выдуманного исследования приведены в таблице:

Содержание вещества B, ммоль/г				Вещество D, ммоль/л
				исходное содержание в крови				прирост концентрации
группа 1	группа 2	группа 3	группа 1		группа 2	группа 3	группа 2		группа 3
1	2	3	4		5	6	7		8
12	8	8	0,7		0,8	0,8	4		4
13	8	9	1,4		0,9	0,9	5		3
14	9	9	1,8		2,5	2,3	4		3,5
15	10	11	1,1		1,2	2,0	3,5		2
14	7	12	1,6		1,3	1,4	5		1
13	7	12	1,7		1,5	1,6	5		1,5
13	9	13	1,3		1,6	1,3	3,5		1
10	9	13	1,4		2,1	1,7	4		1,5
11	11	12	1,5		2,0	1,5	2		2
16	6	11	2,2		1,0	1,6	5		2

Хотим вас предупредить, что выборки объема 10 рассматриваются нами для простоты представления данных и вычислений, на практике такого объема выборок обычно оказывается недостаточно для формирования статистического заключения.

В качестве примера рассмотрим данные 1-го столбца таблицы.

Выборочное среднее вычисляется по формуле:

<X> = (12 + 13 + 14 + 15 + 14 + 13 + 13 + 10 + 11 + 16) / 10 = 13,1;

Выборочная дисперсия данного показателя равна Dx = 3,2; среднеквадратичное отклонение Sx = sqr (Dx) = sqr (3,2) = 1,79 [sqr (x) - функция извлечения квадратного корня из х].

CV = (1,79 / 13,1) * 100% = 13,7; - коэффициент вариации

Ошибка выборочного среднего = 1,79 / sqr (10) = 0,57 [sqr (x)- функция извлечения квадратного корня из х];

Коэффициент Стьюдента t в данном случае для числа степеней свободы f = 10 - 1 = 9 и уровня доверительной вероятности 95% равен 2,26, доверительный интервал для среднего заключен между границами 11,87 и 14,39.

Основные статистики и таблицы

• Описательные статистики

  • "Истинное" среднее и доверительный интервал

  • Форма распределения; нормальность

• Корреляции

  • Определение корреляции

  • Простая линейная корреляция (Пирсона r)

  • Как интерпретировать значения корреляций

  • Значимость корреляций

  • Выбросы

  • Количественный подход к выбросам

  • Корреляции в неоднородных группах

  • Нелинейные зависимости между переменными

  • Измерение нелинейных зависимостей

  • Разведочный анализ корреляционных матриц

  • Построчное удаление пропущенных данных в сравнении с попарным удалением

  • Как определить смещения, вызванные попарным удалением пропущенных данных

  • Попарное удаление пропущенных данных в сравнении с подстановкой среднего значения

  • Ложные корреляции

  • Являются ли коэффициенты корреляции "аддитивными"?

  • Как определить, являются ли два коэффициента корреляции значимо различными

• t-критерий для независимых выборок

  • Цель, предположения

  • Расположение данных

  • Графики t-критериев

  • Более сложные групповые сравнения

• t-критерий для зависимых выборок

  • Внутригрупповая вариация

  • Цель

  • Предположения

  • Расположение данных

  • Матрицы t-критериев

  • Более сложные групповые сравнения

• Внутригрупповые описательные статистики и корреляции (группировка)

  • Цель

  • Расположение данных

  • Статистические тесты для группированных данных

  • Другие близкие методы анализа данных

  • Апостериорные сравнения средних

  • Группировка в сравнении с дискриминантным анализом

  • Группировка в сравнении c таблицами частот

  • Графическое представление группировки

• Таблицы частот

  • Цель

  • Приложения

• Таблицы сопряженности и таблицы флагов и заголовков

  • Цель и расположение данных

  • Таблицы 2x2

  • Маргинальные частоты

  • Проценты по столбцам, по строкам и проценты от общего числа наблюдений

  • Графическое представление таблиц сопряженности

  • Таблицы флагов и заголовков

  • Интерпретация таблиц заголовков

  • Многовходовые таблицы с категориальными переменными

  • Графическое представление многовходовых таблиц

  • Статистики таблиц сопряженности

  • Многомерные отклики и дихотомии

Описательные статистики

"Истинное" среднее и доверительный интервал. Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее. Среднее - очень информативная мера "центрального положения" наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее.Доверительный интервалдля среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия (см.Элементарные понятия статистики), находится "истинное" (неизвестное) среднее популяции. Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнемp=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции. Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он "накрывает" неизвестное среднее популяции, и наоборот. Хорошо известно, например, что чем "неопределенней" прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки (см. такжеЭлементарные понятия статистики). Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок. При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.

Форма распределения; нормальность. Важным способом "описания" переменной является форма ее распределения, которая показывает, с какой частотой значения переменной попадают в определенные интервалы. Эти интервалы, называемые интервалами группировки, выбираются исследователем. Обычно исследователя интересует, насколько точно распределение можно аппроксимировать нормальным (см. ниже картинку с примером такого распределения) (см. такжеЭлементарные понятия статистики). Простые описательные статистики дают об этом некоторую информацию. Например, еслиасимметрия(показывающая отклонение распределения от симметричного) существенно отличается от 0, то распределениенесимметрично, в то время как нормальное распределение абсолютносимметрично. Итак, у симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна. Далее, еслиэксцесс(показывающий "остроту пика" распределения) существенно отличен от 0, то распределение имеет или более закругленный пик, чем нормальное, или, напротив, имеет более острый пик (возможно, имеется несколько пиков). Обычно, если эксцесс положителен, то пик заострен, если отрицательный, то пик закруглен. Эксцесс нормального распределения равен 0.

Более точную информацию о форме распределения можно получить с помощью критериев нормальности(например, критерия Колмогорова-Смирнова или W критерия Шапиро-Уилка). Однако ни один из этих критериев не может заменить визуальную проверку с помощьюгистограммы(графика, показывающего частоту попаданий значений переменной в отдельные интервалы).

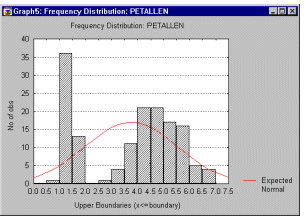
Гистограмма позволяет "на глаз" оценить нормальность эмпирического распределения. На гистограммутакже накладывается кривая нормального распределения. Гистограмма позволяеткачественнооценить различные характеристики распределения. Например, на ней можно увидеть, что распределение бимодально (имеет 2 пика). Это может быть вызвано, например, тем, что выборка неоднородна, возможно, извлечена из двух разных популяций, каждая из которых более или менее нормальна. В таких ситуациях, чтобы понять природу наблюдаемых переменных, можно попытаться найти качественный способ разделения выборки на две части.

В начало

Корреляции

Определение корреляции. Корреляция представляет собой меру зависимости переменных. Наиболее известна корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, винтервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Обратите внимание на крайние значения коэффициента корреляции. Значение -1.00 означает, что переменные имеют строгуюотрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгуюположительную корреляцию. Отметим, что значение 0.00 означает отсутствие корреляции.

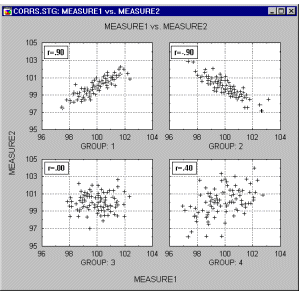
Наиболее часто используемый коэффициент корреляции Пирсона rназывается такжелинейнойкорреляцией, т.к. измеряет степень линейных связей между переменными.

Простая линейная корреляция (Пирсона r). Корреляция Пирсона (далее называемая простокорреляцией) предполагает, что две рассматриваемые переменные измерены, по крайней мере, винтервальной шкале(см.Элементарные понятия статистики). Она определяет степень, с которой значения двух переменных "пропорциональны" друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения вдюймахифунтахили всантиметрахикилограммах.Пропорциональностьозначает простолинейную зависимость. Корреляция высокая, если на графике зависимость "можно представить" прямой линией (с положительным или отрицательным углом наклона).

Проведенная прямая называется прямой регрессииили прямой, построеннойметодом наименьших квадратов. Последний термин связан с тем, что суммаквадратоврасстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной. Заметим, что использованиеквадратоврасстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.

Как интерпретировать значения корреляций. Коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значениекоэффициента детерминацииr²) представляет долю вариации, общую для двух переменных (иными словами, "степень" зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как "величину" корреляции, так и еезначимость.

Значимость корреляций. Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. Как объяснялось выше (см.Элементарные понятия статистики), значимость определенного коэффициента корреляции зависит от объема выборок. Критерий значимости основывается на предположении, что распределение остатков (т.е. отклонений наблюдений от регрессионной прямой) для зависимой переменнойyявляется нормальным (с постоянной дисперсией для всех значений независимой переменнойx). Исследования методом Монте-Карло показали, что нарушение этих условий не является абсолютно критичным, если размеры выборки не слишком малы, а отклонения от нормальности не очень большие. Тем не менее, имеется несколько серьезных опасностей, о которых следует знать, для этого см. следующие разделы.

Выбросы. По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется суммаквадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции.

Заметим ,что если размер выборки относительно мал, то добавление или исключение некоторых данных (которые, возможно, не являются "выбросами", как в предыдущем примере) способно оказать существенное влияние на прямую регресии (и коэффициент корреляции). Это показано в следующем примере, где мы назвали исключенные точки "выбросами"; хотя, возможно, они являются не выбросами, а экстремальными значениями.

Обычно считается, что выбросы представляют собой случайную ошибку, которую следует контролировать. К сожалению, не существует общепринятого метода автоматического удаления выбросов (тем не менее, см. следующий раздел). Чтобы не быть введенными в заблуждение полученными значениями, необходимо проверить на диаграмме рассеяниякаждый важный случай значимой корреляции. Очевидно, выбросы могут не только искусственно увеличить значение коэффициента корреляции, но также реально уменьшить существующую корреляцию.

См. также Доверительный эллипс.

Количественный подход к выбросам. Некоторые исследователи применяют численные методы удаления выбросов. Например, исключаются значения, которые выходят за границы ±2стандартных отклонений(и даже ±1.5 стандартных отклонений) вокруг выборочного среднего. В ряде случаев такая "чистка" данных абсолютно необходима. Например, при изучении реакции в когнитивной психологии, даже если почти все значения экспериментальных данных лежат в диапазоне 300-700миллисекунд, то несколько "странных времен реакции" 10-15секундсовершенно меняют общую картину. К сожалению, в общем случае, определение выбросов субъективно, и решение должно приниматься индивидуально в каждом эксперименте (с учетом особенностей эксперимента или "сложившейся практики" в данной области). Следует заметить, что в некоторых случаях относительная частота выбросов к численности групп может быть исследована и разумно проинтерпретирована с точки зрения самой организации эксперимента. См. такжеДоверительный эллипс.

Корреляции в неоднородных группах. Отсутствие однородности в выборке также является фактором, смещающим (в ту или иную сторону) выборочную корреляцию. Представьте ситуацию, когда коэффициент корреляции вычислен по данным, которые поступили из двух различных экспериментальных групп, что, однако, было проигнорировано при вычислениях. Далее, пусть действия экспериментатора в одной из групп увеличивают значения обеих коррелированных величин, и ,таким образом, данные каждой группы сильно различаются надиаграмме рассеяния(как показано ниже на графике).

В подобных ситуациях высокая корреляция может быть следствием разбиения данных на две группы, а вовсе не отражать "истинную" зависимость между двумя переменными, которая может практически отсутствовать (это можно заметить, взглянув на каждую группу отдельно, см. следующий график).

Если вы допускаете такое явление и знаете, как определить "подмножества" данных, попытайтесь вычислить корреляции отдельно для каждого множества. Если вам неясно, как определить подмножества, попытайтесь применить многомерные методы разведочного анализа (например, Кластерный анализ).

Нелинейные зависимости между переменными. Другим возможным источником трудностей, связанным с линейной корреляциейПирсона r, является форма зависимости. КорреляцияПирсона rхорошо подходит для описания линейной зависимости. Отклонения от линейности увеличивают общую сумму квадратов расстояний от регрессионной прямой, даже если она представляет "истинные" и очень тесные связи между переменными. Итак, еще одной причиной, вызывающей необходимость рассмотрениядиаграммы рассеяниядля каждого коэффициента корреляции, является нелинейность. Например, следующий график показывает сильную корреляцию между двумя переменными, которую невозможно хорошо описать с помощью линейной функции.