Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Брестский Государственный Университет им. А.С. Пушкина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Kr_1

.pdf

Скачиваний:

Добавлен:

11.02.2015

Размер:

352.75 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

	1	14		5	−13	9			1	126 + 70 − 208				1	−12		2
X = −			−10	−4	8			= −			−90	−56 +128	= −		−18		3
	6					14			6					6		=		.
			−2 1		1		16				−18	+14 +16			12		−2

Таким образом

x = 2,y = 3,z = -2.

Ответ: (2,3- 2)

Задание 2. Даны вершины треугольника АВС: А(4;3), В(-3;3), С(2;7). Найти: 1. проекцию вектора AB на вектор BC;

2.площадь треугольника АВС;

3.уравнение стороны АВ;

4.уравнение высоты СН;

5.уравнение медианы АМ;

6.уравнение прямой, проходящей через вершину С параллельно стороне АВ;

7.расстояние от точки С до прямой АВ;

8.сделать чертеж.

Решение

Пр

(из

скалярного произведения

(AB

BC)

Находим

= (−7;0);

= (5;4).

= (−7) 5 + 0 4 = −35 .

= 52 + 42 = 41. Пр

= −

S ABC =

(из векторного произведения

= (7;0) ;

= (5;4).

= 28k

= 28

= 28 ,

=1.

S ABC =

1 28 =14 (ед. кв.).

3) Используем формулу уравнения прямой, проходящей через две точки:

x − x0

y − y0

− x

− y

где A(x0;y0 ), B(x1;y1) .

Тогда

x − 4

y −3

; 6(x − 4) = 7(y −3) ,

−3 − 4

−3 −3

6x −7y −3 = 0 - уравнение прямой АВ.

Для полученного уравнения прямой АВ: kAB

= 6 ; так как CH AB ,

то kCH kAB = −1 (условие перпендикулярности).

kCH

= −1 kCH = −7 .

Тогда

по формуле

уравнения

прямой

проходящей

через

точку

A(x0 ; y0 ) с угловым коэффициентом k: y − y0 = k(x − x0 ) , получим:

y −

7 = −

7 (x − 2) или 7x + 6y −56 = 0 - уравнение высоты СН.

−3 + 2

3 + 7

Найдем

середину

отрезка

ВС

или

точку

;

, т.е.

. Для составления уравнения АМ воспользуемся формулой

M −

уравнения прямой, проходящей через две точки как в пункте 3.

x − 4

y −3

;

x − 4

y −3

;

x − 4

y −3

;

4(x − 4)= −9y + 27 ;

−1 2 −

−9 2

5 −3

−9

4x + 9y − 43 = 0 - уравнение медиана АМ.

Так как kAB =

6 , то уравнение прямой, проходящей через точку С с

таким же угловым коэффициентом имеет вид

y −7 = 6 (x − 2); 6x −7y + 37 = 0 .

Расстояние от точки C(2;7) до прямой АВ: 6x −7y −3 = 0 найдем по

формуле

62 −7 7 −3

d =

≈ 4,34 .

36 + 49

Решение задачи проиллюстрируем на чертеже.

M	A
M
	0

Задание 3. Даны четыре точки: А1(4;7;8), А2(-1;13;0), А3(2;4;9), А4(1;8;9).

Найти: 1. объем пирамиды A1A2A3A4 ;

2.угол между прямыми A1A2 и A1A4 ( в градусах);

3.уравнение плоскости А1, А2; А3;

4.уравнение прямой A4M, перпендикулярной к плоскости

A1A2A3 .

																Решение
1) Найдем объем пирамиды А1А2А3А4 по формуле:
V	=	1														;						= (−5;6;−8);				= (−2;−3;1) ;
V	=	1	A A	2			A A		3		A A				4	;		A A			2	= (−5;6;−8);		A A	3	= (−2;−3;1) ;
пир		6	1	2		1			3			1			4	1					2	1			3
		6																	= (−3;1;1) .
													A1A4						= (−3;1;1) .
																	−5			6		−8
																	−5			6		−8
														=			−2			−3		1	= 20 − 6 + 88 =102 .
		A1A2			A1A3					A1A4				=			−2			−3		1	= 20 − 6 + 88 =102 .
																	−3			1		1
								V				=			1		102			=17 (куб. ед.).
										пир					6

2) Для нахождения угла между прямыми (А1А2) и (А1А4), найдем угол между направляющими векторами этих прямых, т.е. векторами A1A2 и

A1A4 .

			,				)	=			A1A2		A1A4		;
	cosϕ = cos(A A			A A		4

	1	2	1							A1A2				A1A4

cosϕ =	−5 (−3) + 6 1−8 1	=			13							≈ 0.3502 , тогда ϕ ≈ 69D30' .
	25 +36 + 64 9 +1+1			125					11

3) Уравнение плоскости по трем точкам, не лежащим на одной прямой:

A1(x1;y1;z1), A2(x2;y2;z3), A3(x3;y3;z3) находим в виде:

	x − x1	y − y1		z − z1

	x2 − x1	y2 − y1		z2 − z1		= 0.
	x3 − x1	y3 − y1		z3 − z1
		x − 4	y −7		z −8

Для нашего случая имеем:		−5	6		−8		= 0 .
		−2	−3		1

Раскрыв определитель по элементам первой строки, получим:

−18(x − 4) + 21(y −7) + 27(z −8) = 0 или 6(x − 4) −7(y −7) −9(z −8) = 0 6x −7y −9z + 97 = 0 - уравнение плоскости А1А2А3.

4) Составим уравнение прямой А4М перпендикулярной плоскости А1А2А3. Для этого направляющий вектор прямой приравняем к

нормальному вектору плоскости А1А2А3, т.е. S = n = (6;−7;−9).

Уравнение А4М имеет вид:

x 6−1 = y−−78 = z−−99 .

Задание 4. Найти пределы, не пользуясь правилом Лопиталя.

Решение

−

2 +

−

+ 6x −5

∞

а)

lim

= lim

7x2 − x −1

x→∞

∞

x→∞

−

x→∞

−

lim

= 0

x→∞ xn

n > 0;

A = const

(1− 1− x2 )

(1+ 1− x2 )

lim

1− 1− x2

lim

б)

(1+

)

x→0

1− x

= lim

1−(1− x2 )

= lim

x→0 x2(1+ 1− x2 )

x→0 (1+ 1− x2 )

в) lim

1−cos 4x

2 sin2 2x cos2x

2x tg2x

= lim

2x sin2x

x→0

= 2 lim sin2x

lim cos2x = 2 1 1 = 2.

x→0

При решении примера использована обобщенная форма I

замечательного предела

lim sinf(x) =1, при f(x) = 2x ,а также теорема о

f(x)→0

f(x)

пределе непрерывной функции:

lim f(x) = f(x0 ).

5x - 1 2x-3

x→x0

2x-3

∞

5x - 1

г) lim

= (1 )= lim

- 1

lim 1+

5x - 8

x→∞

5x - 8

x→∞

5x-8

lim

7 (2x-3)

(2x-3)

x→∞

5x-8

lim

= lim

5x - 8

x→∞

5x - 8

x→∞

14- 21

lim

5x-8 x→∞

14-0

5- x

lim

= e 5-0

= e 5

e .

5x - 8

x→∞

При вычислении этого предела использована обобщенная форма

второго

замечательного

предела:

lim

f(x)

= e и

теорема о

f(x)→∞

f(x)

пределе показательно-степенной функции:

lim ϕ(x)

lim

ϕ(x)

f(x)

lim f(x) x→x0

x→x0

→x0

где x0 конечная или бесконечно удаленная точка.

Задание 5. Найти производные данных функций

а)

y =

10 +

Решение

Применяя

таблицу

производных

известные

правила

дифференцирования, находим:

3 ′

′

−

y' = 10 +

x x

4 x

−1

−

= x

−

2 = x

−

4x2

б)

y =

1 ln tg

− 1

cos x

2 sin2 x

Решение

1 cos x ′

x ′

1 cos x

′

x ′

y ' =

lntg

−

ln tg

−

sin2 x

2 sin2 x

′

x −cos x

(sin

−

(cos x) sin

ctg

sin4 x

2 x

cos

sin3 x + cos x 2sin x cos x =

ctg

+ sin2 x + 2cos2 x =

2 x

sin4 x

cos

sin3 x

1+ cos2 x

1+cos2 x

2sin3 x

sin x

2sin3 x

sin2 x

sin3 x

sin

cos

2sin x

При нахождении производной воспользовались правилами дифференцирования суммы, дроби, сложной функции и таблицей производных.

в) x2 +3y3 − x2 = 0 . y

Решение

Имеем неявно заданную функцию F(x,y)= 0 . Дифференцируем обе части равенства по x , считая y функцией от x .

2x +3 3y2 y′− 2xyy−2x2y′ = 0.

Применили правила дифференцирования дроби и сложной функции. Выразим из полученного равенства y′:

2x + 9y2 y′− 2x + x2 y′ = 0 . y y2

9y2

y′

− 2x .

′

2xy (1− y)

2x (1− y)y2

2xy (1− y)

y (9y4 + x2 )

9y4 + x2

Задание 6. Найти уравнение касательной, уравнение нормальной

плоскости и вычислить кривизну линии

= (t3 + t −1)Gi +(2t2 + 3t + 2)Gj +(t2 +1)kG, в точке t0 =1.

Решение

Канонические уравнения касательной к кривой

= x(t)i

+ y(t) j

+ z(t)k

точке

M (x

)

имеют

вид

x − x0

y − y0

z − z0

уравнение

′

x (t0 )

y (t0 )

z (t0 )

нормальной плоскости x′(t0 )(x − x0 )+ y′(t0 )(y − y0 )+ z′(t0 )(z − z0 )= 0 .

данном

случае

x(t) = t3 + t −1,

y(t) = 2t2 +3t + 2,

z(t) = t2 +1;

x0 = x(t0 ) = x(1) =1, y0 = y(t0 ) = y(1) = 7 , z0 = z(t0 ) = z(1) = 2; M0(1;7;2).

Найдем

′

x (t) = 3t

+1, y (t) = 4t +3 , z (t) = 2t ;

′

= 2 .

Тогда

x (t0 ) = x (1) = 4, y (t0 ) = y (1)

7 , z (t0 ) = z (1)

x −1

y −7

= z − 2

- уравнения касательной,

(z − 2)= 0 или

4(x −1)+ 7(y −7)+ 2

4x + 7y + 2z −57 = 0 - уравнение нормальной плоскости.

Кривизну пространственной линии r = Gr(t) вычислим по формуле

r′

K =

× r′′

r′

′

′′

Найдем вектора r

′

и r

′′

= x (t)i

+ y (t) j

+ z (t)k

= x (t)i + y (t) j + z (t)k .

+(4t

r′ = (3t

2 +1)i

3) j +

2tk

r′′ = 6t i

+ 4 j

+ 2k .

При t0 =1 получим r′

4 i

+ 7 j

+ 2k

и r′′

6 i + 4 j

2k .

Тогда векторное произведениеG r′G×

Gr′′

равно вектору

r′×r′′ = 4

6 i

4 j

− 26k .

Вычислим модуль векторного произведения

62 + 42 + 262 =

36 +16 + 676 =

729 = 27 .

r′× r′′

и модуль вектора r′:

42 + 72 + 22 =

16 + 49 + 4 =

69 .

Тогда

K =

≈ 0,047 .

(

69 )3

Задание 7. Исследовать на экстремум функцию z = x3 + y3 −3xy +1.

Решение

Найдем частные производные z′x = 3x2 −3y , z′y = 3y2 −3x .

−3y

= 0,

Приравнивая их к нулю, получим систему

−3x

= 0.

3y2

Решая систему методом исключения, находим

y = x2,

= 0,

x =1,

y = x

(

x3 −

)

= 0.

y1 =1.

x4 − x

Таким образом, получим две точки M1(0;0) и M2(1;1), в которых

функция может иметь экстремум.

′′

Найдем вторые частные производные zxx

= 6x , zyy

= 6y , zxy = −3 .

Рассмотрим точку M1(0;0).

′′

Вычислим A = zxx (M1) = 0 , B = zxy (M1) = −3 , A = zxx (M1) = 0 .

Тогда = AC −B2 = −9 .

Так как

< 0 ,

то в точке M (0;0)

экстремума

нет.

′′

В точке M2(1;1), имеем A = zxx (M2 ) = 6 ,

B = zxy (M2 ) = −3 , A = zxx (M2 ) = 6 .

Следовательно

= AC −B2 = 36 −9 = 27 . Так как

> 0 и

A > 0, то в

точке M2(1;1) у функции минимум zmin = z(1;1) = 0.

Ответ: в точке M2(1;1) функция имеет минимум, zmin = z(1;1) = 0.

Задание 8. При различных значениях признака X было 5 раз измерено значение признака Y . Полученные результаты приведены в таблице.

X	1	2	3	4	5
Y	5,5	6,.5	5,0	3,0	3,5

Предполагая, что зависимость между значениями признаков выражается линейной функцией y = a x + b по методу наименьших

квадратов найти параметры a и b . Каково значение признака Y при x = 6 ? Сделать чертеж.

Решение

Наилучшими будут те значения параметров a и b , которые обращают в минимум сумму

S(a,b) = ∑(axi +b − yi )2 .

i=1

В точке минимума

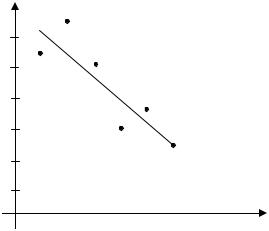
					5	xi2
∂S		= 0,		a	∑i=1	xi2
	∂a	= 0,	или		∑i=1
	∂S		или		5
	∂S	= 0,			5	xi
	∂b	= 0,		a	∑	xi
	∂b				∑
					i=1

Составим расчетную таблицу

+b∑xi = ∑xi yi ,

i=1 i=1 5

+ 5b = ∑yi .

i=1

		x i		2					y i		x i y i
		x i			x i				y i		x i y i
	1			1				5,5			5,5
	2			4				6,5			13,0
	3			9				5,0			15,0
	4			16				3,0			12,0
	5			25				3,5			17,5
В нашем случае	15			55				23,5			63
В нашем случае		система			примет		вид
					55a +15b = 63,
						+ 5b		= 23,5.
					15a	+ 5b		= 23,5.
Так как определитель системы						=			55	15	= 50 ≠ 0 , то система имеет
Так как определитель системы						=			55	15	= 50 ≠ 0 , то система имеет
									15	5
единственное решение.
Так как
1 =		63	15		= −37,5 ,			2 =		55	63	= 347,5 ,
1 =		63	15		= −37,5 ,			2 =		55	63	= 347,5 ,
		23,5	5							15	23,5
то по формулам Крамера
		a =		1 = −0,75 , b =						2 = 6,95 .

Итак, искомая эмпирическая формула имеет вид y = −0,75x + 6,95 .

Вычислим y(6) = −0,75 6 + 6,95 = −4,5 + 6,95 = 2,45 .

Сделаем рисунок

	2	3	4	5		7
1					6		x	29

									Задания для аудиторного занятия
						«Определители. Матрицы. Системы»
1. Вычислить определители:
	2 −3									2	−1		3									1	2			−3


а)					; б)					5	1		2			; в)						3	0				1	.
	1		−5							−3	2	−4										−1	−2				4
										−3	2	−4										−1	−2				4
Ответ: а) –7; б) 9; в) –6.
2. Вычислить							определители												методы							разложения							по		строке						или
столбцу:			−1																	−1
	2					0			;			б)			1								0	.
	2					0									1								0
а)	0 1 −1														−1 1 2
	3		2			−2									0					3			1
Ответ: а) 3; б) –6.
														−1							2						2		−1
3. Найти 3A −2B, если A =																	3						, B =				0		4
3. Найти 3A −2B, если A =																	3			0			, B =				0		4	.
																	4										0		−2
																	4			−1							0		−2
		−7				8
Ответ:			3		−8
Ответ:			3		−8			.
			12		1
			12		1
4. Найти произведение матриц:
	−1 2						0 6							−1 3 0													0				0 1 3						0		−1
а)		0		3		×	0 6										4 5 1								×		1		; в)		0 1 3					×		1 2				.
а)		0		3		×					; б)						4 5 1								×		1		; в)			−1 2 4				×		1 2				.
									2 −1																							−1 2 4
		−1 4															0			−1 2																		6 3
		−1 4															0			−1 2							−1											6 3
			4			−8						3							19				11
				6		−3						4		; в)					19				11
Ответ: а)				6		−3				; б)		4		; в)											.
				8		10													26				17
				8		10					−3
																									−1 3								−1				−1		3
5. Найти обратную матрицу A																		−1		: а) A =					−1 3												2		4
5. Найти обратную матрицу A																				: а) A =									;		б) A = −1						2		4	.
																										−2			4					1			−1		0
																																		1			−1		0
				2		−		3				−4 7 3 7 6 7
				2		−		2				−4 7 3 7 6 7
Ответ: а)								2				−7 7						3 7
Ответ: а)								1		; б)		−7 7						3 7					−1 7 .
				1		−		1				1 7 1 7 2 7
				1		−		2				1 7 1 7 2 7
								2

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.02.2015113.66 Кб32KONTROL_NAYa_RABOTA_fizika.doc
#
19.09.201936.77 Кб23kontr_po_politologii.docx
#
11.02.2015232.62 Кб255Kraevedenie.docx
#
24.04.201966.97 Кб24kratkie_otvety_po_obshey_1_semestr.docx
#
13.11.201957.3 Кб5krug_umel_ruki.docx
#
11.02.2015352.75 Кб14Kr_1.pdf
#
11.02.201570.81 Кб44KurSOVAYa_33__33__33.docx
#
17.11.2019112.16 Кб5KURSOVAYa_PO_MUZ_KE_proverennoe_3_raz.docx
#
11.02.2015191.49 Кб15KursRABOTA-OBRAZETs.doc
#
11.02.20151.02 Mб24kurs_lekciy_up.pdf
#
10.02.2015245.25 Кб20kurs_lektsy_sotsiologia_20_chasov.doc